线性规划问题的实际应用
王震


线性规划是现代数学中研究最优化理论的重要模型.它的实际运用范围十分广泛,从解决技术问题的最优化到工业、农业、商业、交通运输、经济、军事等众多领域都发挥作用.简单线性规划这部分内容体现了新教材重视数学应用,重视知识的发生发展过程,贴近生活的特点.为了让学生学好简单线性规划知识,提高学生运用线性规划知识解决实际问题的能力,本文对高中数学中线性规划问题的应用进行了剖析,对此类问题的求解思想和一般步骤作了较详细地阐述.
1整数最优解的确定
求最优解的问题,特别是当实际问题要求最优解是整数时,这是线性规划问题图解法中最重要而且是最难完成的一个环节,怎样来确定符合条件的整数最优解呢?主要方法有四:
(1)直接求解法,适用于多边形的角点坐标恰好是整数最优解;
(2)观察法,此法适用于由可行域直接可看出的;
(3)边界找点法;
(4)进一法或去尾法.后两种方法是不能直接求得又不能由图看出的情况下来运用的.
它既需要由图形的直观性又需要适当的计算,應用数形结合的数学思想.
例1某运输公司有7辆载重6t的A型卡车,4辆载重10t的B型卡车,有9名驾驶员.在建造某段高速公路中,公司承包了每天至少运输沥青360t的任务.已知每辆卡车每天往返次数为A型8次,B型6次,每天运输成本为A型160元,B型252元.每天应派出A型、B型车各多少辆,能使公司总成本最低.
解分析列表如下:
表1
类别
车辆车辆数载重量往返次数A型车辆x768B型车辆y4106设派A型车x辆,B型车y辆.
则线性约束条件为:
图1x+y≤9,
0≤x≤7,
0≤y≤4,
8×6x+6×10y≥360.
画出可行域:
如图1所示的阴影部分,即四边形ABCD.
目标函数:z=160x+252y.
由图1可知,当l:160x+252y=0向右上方平移至l′的位置时,直线经过可行域上的点A,y轴截距b=1252z最小,即z最小.
由方程组4x+5y=30,
x=7.
解得点A(7,25).25不是整数.调整,整数解为最优点E(5,2).
当x=5,y=2时,总成本z=160×5+252×2=1304(元).此时运输沥青吨数为8×6×5+6×10×2=360(t).
即每天应派A型车5辆,B型车2辆,总成本1304元最低,并能运沥青360吨.
在上述解答中,虽然可行域给出目标函数z的最小值,但不符合实际问题的最优解是非负整数的条件,这时应该进行调解.“就近原则”.本题中与点A最近的整点是F(7,1),此时总成本z=160×7+252×1=1352(元),比 z=1304(元)高,所以调整的关键是寻求与可行域边界接近的整点(不妨简称边界找点法).也就是缩小可行域来寻找它的整数解,如果整点数不止一个,则逐个比较目标函数的取值,确定最优整点,得到最优解.
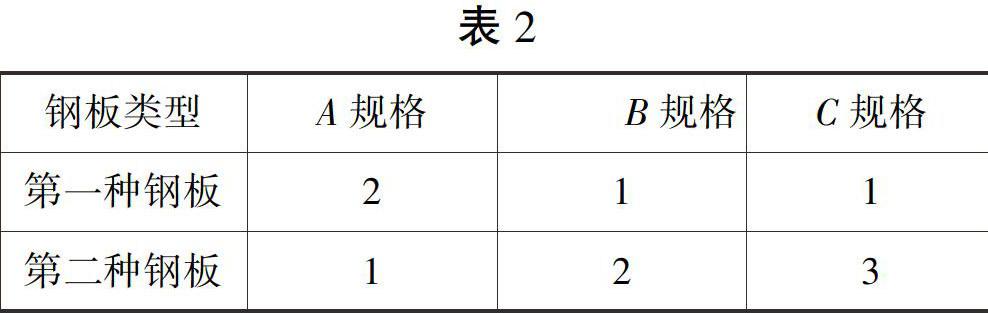
例2要将两种大小不同的钢板截成A、B、C三种规格,每张钢板可同时截得三种不规格的小钢板的块数如下表所示:
表2
钢板类型A规格B规格C规格第一种钢板211第二种钢板123解今需要A、B、C三种规格的成品分别为15、18、27块,问各截这两种钢板多少张可得所需的三种规格的成品,且使所用钢板张数最少解:
设两种钢板分别要x,y张,则其线性约束条件为:
2x+y≥15,
x+2y≥18,
x+3y≥27,
x≥0,y≥0.作出可行域如图2所示,
图2其目标函数为z=x+y.
(那么,怎样寻找其最优整数点呢?分解小步骤如下:)(步骤1)作出一组平行直线x+y=t中经过可行域内的点且和原点距离最近的直线;
(步骤2)此直线经过直线x+3y=27和直线2x+y=15的交点A(185,395);
(步骤3) 过交点A(185,395)的目标函数线的方程为x+y=575;
(步骤4) 由于185,395都不是整数,所以可行域内的点A(185,395)不是最优解;
(步骤5) 找出与575=11.4(x+y=575)接近的,且适合题意的整数解(此法简称为进一法或去尾法).经过可行域内的整点且与原点距离最近的直线是x+y=12;
(步骤6) 所以适合题意的整点为B(3,9),C(4,8),即为所求最优解.
2阴影部分面积的确定
例3在直角坐标平面内,有两个区域M和N,M是由y≥0和y≤x,y≤2-x这三个不等式确定;N是随t而变化的区域,它由不等式t≤x≤t+1决定,t的取值范围0≤t≤1,求M和N的公共部分的面积S(t).
解设定区域M为不等式组y≥0,
y≤x,
y≤2-x,
所围成的区域,即△AOB所围成的区域(含边界)(图3).图3 动区域N是两条动直线x=t,x=t+1(0≤t≤1)所构成的带状域.
因此,M和N的公共部分为图3的阴影部分(含边界)的面积,此面积为两个梯形面积之并.
即S(t)=12(1+t)(1-t)+12[1+(1-t)]t =-t2+t+12(0≤t≤1).
3参数取值范围的确定
例4如图4所示,当方程x2+ax+b=0的一根在-2和-1之间,另一根在1和2之间时,用图形表示以a,b为坐标的点(a,b)的存在范围.
解如图4,设fx=x2+ax+b,依题意,得
f(-2)=4-2a+b>0,
f(-1)=1-a+b<0,
f(1)=1+a+b<0,
f(2)=4+2a+b>0.即b>2a-4,
bb<-a-1,
b>-2a-4.图4图5在a,b坐标平面内作出该不等式组的平面区域如图5的阴影部分(不包括边界)为(a,b)的取值范围.
二元一次不等式组的平面区域,实际上就是二元一次不等式组的几何表示.解题时,依题意,作出约束条件的公共部分,就能直观地解决所求问题.
中学数学中的线性规划内容既给传统的教材注入了新鲜的“血液”,又给学生提供了学数学、用数学的实践机会,同时促进了与不等式、方程、函数等知识的整合.通过本知识的学习,学生将初步掌握线性规划的一些基本理论、一般方法,将为线性规划知识的后续学习打下基础,为线性规划知识的广泛应用拿到一枚入门的钥匙.
立体几何中动点轨迹度量问题的探究
安徽省池州一中247000吴成強
青岛市66中266000刘恒荣
立体几何中动点轨迹问题是一个有趣和值得研究的问题,在高考中也注重考查.关于动点轨迹的长度、面积、体积及它们的最值等度量问题的求解,不少学生还是感到有一些困难,其主要原因是对轨迹图形难以弄清.而要明了轨迹图形的形状,需要有一定的空间想象能力和逻辑推理能力,需要积累一定的解题经验,掌握一定的技巧和方法.本文对立体几何中轨迹度量问题做一些探究,起一点抛砖引玉的作用.
1动点轨迹的长度
动点轨迹的长度计算,关键是要弄清轨迹图形的形状.常见轨迹图形的长度计算,主要是线段、圆(或圆弧)的长度的计算.
例1已知四面体ABCD中,DA=DB=DC=1,且DA、DB、DC两两互相垂直,在该四面体表面上与点A的距离是233的点形成一条曲线,这条曲线长度是()
A.32πB.3πC.536πD.33π
图1解析如图1,AE=AF=AH=AG=233,DH=DG=33,AB=AC=BC=2,cos∠DAH=DAAH=1233=32,
所以∠DAH=π6,所以∠EAH=π4-π6=π12.
同理∠GAF=π12,动点形成的轨迹图形为EF,FG,GH,HE,其中EF,EH,FG均是以A为圆心的圆弧,GH是以D为圆心的圆弧,轨迹长度为l=(π3+π12+π12)·233+π2·33=32π,故选A.
评注学生做这道题普遍感到困难的是弄不清轨迹图形的形状,尤其是GH弧,它是以D为圆心、DH为半径的圆弧,学生容易出错.这道题对空间想象能力有较高的要求.
图2例2正方体的棱长为3,A为顶点,P点在正方体表面上运动,PA=2,求P点运动轨迹长度.
解析如图2所示,轨迹图形是由6条圆弧组成,不含A点的正方体三个面上运动轨迹为EN,FG,MH,其长度均为π2·1=π2,含A点的正方体三个面上运动轨迹为EF,GH,MN,其长度均为π6·2=π3,所以所求轨迹图形的长度为l=3×π2+3×π3=5π2.
评注本题用到分类讨论思想,分含A点的正方体三个面上运动轨迹和不含A点的正方体三个面上运动轨迹.含A点的正方体三个面上运动轨迹是以A点为圆心,圆心角均为π6,不含A点的正方体三个面上运动轨迹不是以A点为圆心,而是分别以另外三个直角顶点为圆心,圆心角均为π2.学生对这些轨迹图形容易搞错,这需要有一定的空间想象能力和逻辑推理能力.
图3例3已知正方体ABCD-A1B1C1D1的棱长为2,M为BC的中点,P为正方体内切球球面上任一点,C1M⊥DP,求动点P的轨迹图形的长度.
解析如图3,取AA1中点E,BB1中点F,易知C1M⊥平面CDEF,所以P点的轨迹就是平面CDEF截正方体内切球所得的截面圆,易知正方体内切球半径R=1,设BC1∩B1C=O1,则O1点到FC的距离d即为球心O到平面CDEF的距离.
根据面积关系,得12×1×2=12×CF×CB1×sin∠FCB1=12×5×22×sin∠FCB1,所以sin∠FCB1=110,d=O1C·sin∠FCB1=2×110=15.
所以截面圆的半径r=R2-d2=1-15=255,所以P点轨迹长度为2πr=455π.
评注 P点是动点,直线DP是动直线,而直线C1M是定直线,因此要保证C1M⊥DP,就必须满足定直线C1M垂直于动直线DP所扫过的平面,这个平面就是CDEF平面,又P为正方体内切球球面上任一点,所以P点的轨迹图形就是平面CDEF截球面所得的小圆,而要求小圆的半径,就是要求出球心到截面圆的距离d,学生对这种层层逼近、不断深入的思维过程往往感到有些困难,对学生空间想象能力和合理运算能力也有较高的要求.
图4例4如图4,矩形ABCD中,AB=2BC=4,E为AB的中点,将△ADE的沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻转一周的过程中:
①BM是定值;②点M在某个球面上运动;③存在某个位置,使MB∥平面A1DE;④动点A1的轨迹为球面上的一个小圆,其长度为2π.其中正确的命题是.
解析坐标系建立如图所示,易知A1点的轨迹是yoz坐标平面上以O为圆心,以2为半径的圆,其坐标为(0,2cosθ,2sinθ),C点的坐标为(2,22,0),M点的坐标为(22,2+22cosθ,22sinθ),B点的坐标为(22,2,0),易得BM=3222+22cosθ2+22sinθ2=5,由此可知BM是定值,所以①正确;点M在以B为球心,以为5半径球面上运动,所以②正确;取线段A1D的中点N,则MN是△A1CD的中位线,MN∥CD,所以MN∥BE且有MN=BE,所以四边形BMNE为平行四边形,所以MB∥NE,又NE在平面A1DE内,所以存在某个位置,使MB∥平面A1DE,故③正确;
设M点的坐标为(x,y,z),则有x=22, y=2+22cosθ,z=22sinθ,
所以有(y-2)2+z2=22cosθ2+22sinθ2=12,故点的轨迹是半径为22的圆,其长度为2π,故④正确.
评注本题的关键在于恰当地建立空间直角坐标系,利用空间向量和坐标法的思想巧妙解决问题.本题也可以先验证③正确,再根据③得出①与②是正确的.
2动点轨迹长度的最值
动点轨迹长度最值问题,常常需要利用几何体的侧面(或表面)展开图,或者将有关的平面进行旋转,使一个平面处在另一个平面延展面的位置,然后再利用几何中最小长度原理(即平面上连接两点间的直线段最短)求解.解决这类问题的关键就是要会利用几何体的展开图,教师要强化学生利用侧面(或表面)展开图解决最值问题的意识,使学生熟练地掌握这一方法.
例5已知正三棱锥P-ABC的侧棱长均为a为,∠APB=∠APC=∠BPC=40°,一动点M从A点出发,绕侧面一周回到A点,求动点M轨迹长度的最小值.
图5 解析如图5所示,将三棱锥沿侧棱PA剪开摊平得到侧面展开图,易知∠APA′=120°,PA=PA′=a,线段AA′即为动点M轨迹长度最小值,易得AA′=3a,所以动点M轨迹长度最小 值为3a.
评注解决本题的关键是利用侧面展开图,这是求侧面上轨迹图形长度最值问题的最有效、最简便的方法,要训练学生牢固掌握这一方法.
例6已知圆台的上、下底面半径分别为2cm,4cm,AB是侧面上的母线,AB=6cm,一质点从点B绕侧面一周运动到A点,求质点运动轨迹的最小值.
图6解析如图6,把 圆台补成圆锥,沿母线SAB剪开摊平,侧面展开图如图所示,易知∠BSB′=2π3,线段BA′与AA′相交,设M为AA′上任一点,∠BSM=x,则∠A′SM=2π3-x,SA′=6,SB=12,y=BM+MA′=180-144cosx+6·(2π3-x),y′=144sinx2180-144cosx-6.
由y′=0得2sinx=5-4cosx,4cos2x-4cosx+1=0,cosx=12,x=π3,易知y在[0,π3] 递减,在[π3,2π3]递增,所以当x=π3时,ymin=63+2π.
易知,此时BM为AA′的切线,M为切点.
评注因为线段BA′ 与AA′ 弧相交,所以直接求线段BA′ 的长度是错误的,而这恰恰是很多学生所容易犯的错误.运动轨迹长度要想最小,质点必须从B点运动到AA′ 弧上一点M处,再从M点沿MA′ 弧运动到A′点.M点在AA′ 弧上的何处,需要通过列函数式求解.求解的结果可以看出,BM与AA′ 弧相切,这是一个很好的结论,值得体会.
3动点轨迹图形的面积
动点轨迹图形面积问题,一般是动直线所扫过的图形,求解关键是要弄清动点或动直线所扫过的轨迹图形的形状,这需要有一定的空间想象能力和逻辑推理能力.常见的轨迹图形主要是三角形、四边形、圆面、球面等.
例7在棱长为1的正方体ABCD-A1B1C1D1中,P、Q分别是线段AD1和B1C上的动点,且满足AP=B1Q,P、Q在運动过程中,求线段PQ在平面BCC1B1内的射影所形成的面积.
解析如图7,易知P点在平面BCC1B1内的射影P′ 落在线段BC1上,且BP′=AP=B1Q,所以P′Q∥BB1,图7所以PQ在运动过程中射影P′Q形成的轨迹图形为△OBB1和△OCC1,所以所求轨迹图形面积为S=12×1×1=12.
评注本题解决的关键是要弄清P、Q在运动过程中,线段PQ在平面BCC1B1内的射影图形是什么形状,从教学实践情况来看,学生对PQ在运动过程中射影P′Q满足P′Q∥BB1感到有一点困难.
例8已知正方体ABCD-A1B1C1D1的棱长为4,长为2的线段的两端点P、Q分别在棱DD1上和面ABCD内运动,求PQ中点M形成的轨迹图形的面积.
图8解析易知DD1⊥面ABCD,∠PDQ=90°所以DM=12PQ=1,
所以M点形成的轨迹图形是以D为球心,1为半径的18球面.
S=18×4π×12=π2.
评注解决这类问题要用到立体几何线面垂直的有关性质得出PD⊥DQ,再根据直角三角形斜边的中线等于斜边的一半,得出DM=1,从而得出M点形成的轨迹图形是以D为球心,1为半径的18球面,问题迎刃而解.
4动点轨迹图形的面积的最值
动点轨迹图形面积最值问题的求解,首先需要弄清动点或动直线所扫过的轨迹图形的形状,然后列出面积关系式,再根据有关的数学知识求得面积的最值.有些问题可直接根据几何图形的特点,得出面积的最值.
例9已知长方体ABCD—A1B1C1D1中,AB=AD=4,AA1=1,F为AD上的动点,且AF=λAD(0≤λ≤12),E为底面ABCD的中心,P为正方体表面上的动点,且满足A1P=xAF+yAE(x,y∈R),求动直线A1P所扫过的平面图形面积的最小值.
图9解析如图9所示,易知A1P所扫过平面图形为平行四边行A1FMG,建立空间直角坐标系, 易知A1(0,0,0),F(0,4λ,1),E(2,2,1)
a=A1F=(0,4λ,1),
b=AG=FM=2FE=2(2,2-4λ,0)
a·b=16λ-32λ2,a2=16λ2+1,b2=32(2λ2-2λ+1).
设a与b夹角为θ,则
S=a·b·sinθ=a·b·1-cos2θ
=a2·b2-(a·b)2
=(16λ2+1)·32·(2λ2-2λ+1)-(16λ-32λ2)2
=420λ2-4λ+2=420(λ-110)2+95
因为0≤λ≤12,所以当λ=110时,Smin=495=1255.
评注本题解决的关键是要弄清动直线A1P所扫过的平面图形的形状,而面积关系式则通过建立空间直角坐标系,利用空间向量的办法得出,这一方法对本题的求解显得比较巧妙,值得体会和总结.
5动点轨迹图形的体积或体积的最值
动点轨迹图形的体积或体积的最值问题,需要分析几何体的形状,恰当选择几何体的底面和高,使问题求解变得简便.
例10在棱长为1的正方体ABCD-A1B1C1D1中,P1、P2分别是线段AB和BD1上的动点,且不包括端点,在P1、P2运动过程中,图10线段P1P2始终平行于平面A1ADD1,求动点P1、P2和定点A、B1所形成的几何体P1P2AB1体积的最大值.
解析如图10,作P2O⊥平面ABB1A1,O为垂足,设AP1=x,则P1B=1-x,由△BP1P2∽△BAD1得P1P2AD1=P1BBA=1-x,由△OP1P2∽△A1AD1得OP2A1D1=P1P2AD1=1-x,所以OP2=(1-x)A1D1=1-x,VP2-P1AB1=13·S△P1AB1·OP2=13·12·x·1·(1-x)=16x(1-x)≤16·(x+1-x2)2=124.
等号成立的条件为x=1-x,即x=12.
评注解决本题的关键是要列出体积关系式.抓住动线段P1P2始终平行于平面A1ADD1这一条件,得出△OP1P2∽△A1AD1,从而找到相关线段的数量关系,再选择以P2为顶点,△P1AB1为底面,则容易列出体积关系式.根据体积关系式,不难求出体积的最大值.
例11已知正方形ABCD的边长为6,空间有一點M(不在平面ABCD内),满足MA+MB=10,求三棱锥M—ABC的体积的最大值.
解析由MA+MB=10知动点M的轨迹是以A、B为焦点的椭球面,椭圆的长半轴长a=5,短半轴长b=4,动点M到底面ABC距离的最大值为椭圆的短半轴长4,所以体积的最大值为
Vmax=13·12·6·6·4=24.
评注本题动点M的轨迹是根据椭圆定义得出的,体现了立体几何与解析几何交汇,是高考命题的新动向,也对考生的综合运用知识解决问题的能力提出了较高的要求.
立体几何中有关动点轨迹问题还有很多方面,它们往往比较新颖灵活,对空间想象能力和逻辑推理能力有较高要求,也需要有较强的创新意识.数学之魅力,体现在数学有很强的内在规律,教师要引导学生挖掘数学中所隐含的内在规律,使学生掌握研究数学的思想方法,理解数学的精髓,感悟数学的内在美,并在问题的解决中体验成功的快乐,激发探究的热情和动力,不断发展创造力.
作者简介吴成强(1963—),男,正高级教师,安徽省特级教师,安徽省池州市首届拔尖人才,池州市首批名师工作室主持人,池州市学科带头人,池州市优秀教师,十佳教师,安徽省教坛新星,安徽省先进工作者(省劳模),全国五一劳动奖章获得者,第十届苏步青数学教育奖获得者,2014年安徽省教育年度人物.在《中学数学杂志》等省级以上刊物发表学术论文70多篇,有两篇论文被中国人民大学书报资料中心《高中数学教与学》全文转载.



线性规划是现代数学中研究最优化理论的重要模型.它的实际运用范围十分广泛,从解决技术问题的最优化到工业、农业、商业、交通运输、经济、军事等众多领域都发挥作用.简单线性规划这部分内容体现了新教材重视数学应用,重视知识的发生发展过程,贴近生活的特点.为了让学生学好简单线性规划知识,提高学生运用线性规划知识解决实际问题的能力,本文对高中数学中线性规划问题的应用进行了剖析,对此类问题的求解思想和一般步骤作了较详细地阐述.
1整数最优解的确定
求最优解的问题,特别是当实际问题要求最优解是整数时,这是线性规划问题图解法中最重要而且是最难完成的一个环节,怎样来确定符合条件的整数最优解呢?主要方法有四:
(1)直接求解法,适用于多边形的角点坐标恰好是整数最优解;
(2)观察法,此法适用于由可行域直接可看出的;
(3)边界找点法;
(4)进一法或去尾法.后两种方法是不能直接求得又不能由图看出的情况下来运用的.
它既需要由图形的直观性又需要适当的计算,應用数形结合的数学思想.
例1某运输公司有7辆载重6t的A型卡车,4辆载重10t的B型卡车,有9名驾驶员.在建造某段高速公路中,公司承包了每天至少运输沥青360t的任务.已知每辆卡车每天往返次数为A型8次,B型6次,每天运输成本为A型160元,B型252元.每天应派出A型、B型车各多少辆,能使公司总成本最低.
解分析列表如下:
表1
类别
车辆车辆数载重量往返次数A型车辆x768B型车辆y4106设派A型车x辆,B型车y辆.
则线性约束条件为:
图1x+y≤9,
0≤x≤7,
0≤y≤4,
8×6x+6×10y≥360.
画出可行域:
如图1所示的阴影部分,即四边形ABCD.
目标函数:z=160x+252y.
由图1可知,当l:160x+252y=0向右上方平移至l′的位置时,直线经过可行域上的点A,y轴截距b=1252z最小,即z最小.
由方程组4x+5y=30,
x=7.
解得点A(7,25).25不是整数.调整,整数解为最优点E(5,2).
当x=5,y=2时,总成本z=160×5+252×2=1304(元).此时运输沥青吨数为8×6×5+6×10×2=360(t).
即每天应派A型车5辆,B型车2辆,总成本1304元最低,并能运沥青360吨.
在上述解答中,虽然可行域给出目标函数z的最小值,但不符合实际问题的最优解是非负整数的条件,这时应该进行调解.“就近原则”.本题中与点A最近的整点是F(7,1),此时总成本z=160×7+252×1=1352(元),比 z=1304(元)高,所以调整的关键是寻求与可行域边界接近的整点(不妨简称边界找点法).也就是缩小可行域来寻找它的整数解,如果整点数不止一个,则逐个比较目标函数的取值,确定最优整点,得到最优解.
例2要将两种大小不同的钢板截成A、B、C三种规格,每张钢板可同时截得三种不规格的小钢板的块数如下表所示:
表2
钢板类型A规格B规格C规格第一种钢板211第二种钢板123解今需要A、B、C三种规格的成品分别为15、18、27块,问各截这两种钢板多少张可得所需的三种规格的成品,且使所用钢板张数最少解:
设两种钢板分别要x,y张,则其线性约束条件为:
2x+y≥15,
x+2y≥18,
x+3y≥27,
x≥0,y≥0.作出可行域如图2所示,
图2其目标函数为z=x+y.
(那么,怎样寻找其最优整数点呢?分解小步骤如下:)(步骤1)作出一组平行直线x+y=t中经过可行域内的点且和原点距离最近的直线;
(步骤2)此直线经过直线x+3y=27和直线2x+y=15的交点A(185,395);
(步骤3) 过交点A(185,395)的目标函数线的方程为x+y=575;
(步骤4) 由于185,395都不是整数,所以可行域内的点A(185,395)不是最优解;
(步骤5) 找出与575=11.4(x+y=575)接近的,且适合题意的整数解(此法简称为进一法或去尾法).经过可行域内的整点且与原点距离最近的直线是x+y=12;
(步骤6) 所以适合题意的整点为B(3,9),C(4,8),即为所求最优解.
2阴影部分面积的确定
例3在直角坐标平面内,有两个区域M和N,M是由y≥0和y≤x,y≤2-x这三个不等式确定;N是随t而变化的区域,它由不等式t≤x≤t+1决定,t的取值范围0≤t≤1,求M和N的公共部分的面积S(t).
解设定区域M为不等式组y≥0,
y≤x,
y≤2-x,
所围成的区域,即△AOB所围成的区域(含边界)(图3).图3 动区域N是两条动直线x=t,x=t+1(0≤t≤1)所构成的带状域.
因此,M和N的公共部分为图3的阴影部分(含边界)的面积,此面积为两个梯形面积之并.
即S(t)=12(1+t)(1-t)+12[1+(1-t)]t =-t2+t+12(0≤t≤1).
3参数取值范围的确定
例4如图4所示,当方程x2+ax+b=0的一根在-2和-1之间,另一根在1和2之间时,用图形表示以a,b为坐标的点(a,b)的存在范围.
解如图4,设fx=x2+ax+b,依题意,得
f(-2)=4-2a+b>0,
f(-1)=1-a+b<0,
f(1)=1+a+b<0,
f(2)=4+2a+b>0.即b>2a-4,
bb<-a-1,
b>-2a-4.图4图5在a,b坐标平面内作出该不等式组的平面区域如图5的阴影部分(不包括边界)为(a,b)的取值范围.
二元一次不等式组的平面区域,实际上就是二元一次不等式组的几何表示.解题时,依题意,作出约束条件的公共部分,就能直观地解决所求问题.
中学数学中的线性规划内容既给传统的教材注入了新鲜的“血液”,又给学生提供了学数学、用数学的实践机会,同时促进了与不等式、方程、函数等知识的整合.通过本知识的学习,学生将初步掌握线性规划的一些基本理论、一般方法,将为线性规划知识的后续学习打下基础,为线性规划知识的广泛应用拿到一枚入门的钥匙.
立体几何中动点轨迹度量问题的探究
安徽省池州一中247000吴成強
青岛市66中266000刘恒荣
立体几何中动点轨迹问题是一个有趣和值得研究的问题,在高考中也注重考查.关于动点轨迹的长度、面积、体积及它们的最值等度量问题的求解,不少学生还是感到有一些困难,其主要原因是对轨迹图形难以弄清.而要明了轨迹图形的形状,需要有一定的空间想象能力和逻辑推理能力,需要积累一定的解题经验,掌握一定的技巧和方法.本文对立体几何中轨迹度量问题做一些探究,起一点抛砖引玉的作用.
1动点轨迹的长度
动点轨迹的长度计算,关键是要弄清轨迹图形的形状.常见轨迹图形的长度计算,主要是线段、圆(或圆弧)的长度的计算.
例1已知四面体ABCD中,DA=DB=DC=1,且DA、DB、DC两两互相垂直,在该四面体表面上与点A的距离是233的点形成一条曲线,这条曲线长度是()
A.32πB.3πC.536πD.33π
图1解析如图1,AE=AF=AH=AG=233,DH=DG=33,AB=AC=BC=2,cos∠DAH=DAAH=1233=32,
所以∠DAH=π6,所以∠EAH=π4-π6=π12.
同理∠GAF=π12,动点形成的轨迹图形为EF,FG,GH,HE,其中EF,EH,FG均是以A为圆心的圆弧,GH是以D为圆心的圆弧,轨迹长度为l=(π3+π12+π12)·233+π2·33=32π,故选A.
评注学生做这道题普遍感到困难的是弄不清轨迹图形的形状,尤其是GH弧,它是以D为圆心、DH为半径的圆弧,学生容易出错.这道题对空间想象能力有较高的要求.
图2例2正方体的棱长为3,A为顶点,P点在正方体表面上运动,PA=2,求P点运动轨迹长度.
解析如图2所示,轨迹图形是由6条圆弧组成,不含A点的正方体三个面上运动轨迹为EN,FG,MH,其长度均为π2·1=π2,含A点的正方体三个面上运动轨迹为EF,GH,MN,其长度均为π6·2=π3,所以所求轨迹图形的长度为l=3×π2+3×π3=5π2.
评注本题用到分类讨论思想,分含A点的正方体三个面上运动轨迹和不含A点的正方体三个面上运动轨迹.含A点的正方体三个面上运动轨迹是以A点为圆心,圆心角均为π6,不含A点的正方体三个面上运动轨迹不是以A点为圆心,而是分别以另外三个直角顶点为圆心,圆心角均为π2.学生对这些轨迹图形容易搞错,这需要有一定的空间想象能力和逻辑推理能力.
图3例3已知正方体ABCD-A1B1C1D1的棱长为2,M为BC的中点,P为正方体内切球球面上任一点,C1M⊥DP,求动点P的轨迹图形的长度.
解析如图3,取AA1中点E,BB1中点F,易知C1M⊥平面CDEF,所以P点的轨迹就是平面CDEF截正方体内切球所得的截面圆,易知正方体内切球半径R=1,设BC1∩B1C=O1,则O1点到FC的距离d即为球心O到平面CDEF的距离.
根据面积关系,得12×1×2=12×CF×CB1×sin∠FCB1=12×5×22×sin∠FCB1,所以sin∠FCB1=110,d=O1C·sin∠FCB1=2×110=15.
所以截面圆的半径r=R2-d2=1-15=255,所以P点轨迹长度为2πr=455π.
评注 P点是动点,直线DP是动直线,而直线C1M是定直线,因此要保证C1M⊥DP,就必须满足定直线C1M垂直于动直线DP所扫过的平面,这个平面就是CDEF平面,又P为正方体内切球球面上任一点,所以P点的轨迹图形就是平面CDEF截球面所得的小圆,而要求小圆的半径,就是要求出球心到截面圆的距离d,学生对这种层层逼近、不断深入的思维过程往往感到有些困难,对学生空间想象能力和合理运算能力也有较高的要求.
图4例4如图4,矩形ABCD中,AB=2BC=4,E为AB的中点,将△ADE的沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻转一周的过程中:
①BM是定值;②点M在某个球面上运动;③存在某个位置,使MB∥平面A1DE;④动点A1的轨迹为球面上的一个小圆,其长度为2π.其中正确的命题是.
解析坐标系建立如图所示,易知A1点的轨迹是yoz坐标平面上以O为圆心,以2为半径的圆,其坐标为(0,2cosθ,2sinθ),C点的坐标为(2,22,0),M点的坐标为(22,2+22cosθ,22sinθ),B点的坐标为(22,2,0),易得BM=3222+22cosθ2+22sinθ2=5,由此可知BM是定值,所以①正确;点M在以B为球心,以为5半径球面上运动,所以②正确;取线段A1D的中点N,则MN是△A1CD的中位线,MN∥CD,所以MN∥BE且有MN=BE,所以四边形BMNE为平行四边形,所以MB∥NE,又NE在平面A1DE内,所以存在某个位置,使MB∥平面A1DE,故③正确;
设M点的坐标为(x,y,z),则有x=22, y=2+22cosθ,z=22sinθ,
所以有(y-2)2+z2=22cosθ2+22sinθ2=12,故点的轨迹是半径为22的圆,其长度为2π,故④正确.
评注本题的关键在于恰当地建立空间直角坐标系,利用空间向量和坐标法的思想巧妙解决问题.本题也可以先验证③正确,再根据③得出①与②是正确的.
2动点轨迹长度的最值
动点轨迹长度最值问题,常常需要利用几何体的侧面(或表面)展开图,或者将有关的平面进行旋转,使一个平面处在另一个平面延展面的位置,然后再利用几何中最小长度原理(即平面上连接两点间的直线段最短)求解.解决这类问题的关键就是要会利用几何体的展开图,教师要强化学生利用侧面(或表面)展开图解决最值问题的意识,使学生熟练地掌握这一方法.
例5已知正三棱锥P-ABC的侧棱长均为a为,∠APB=∠APC=∠BPC=40°,一动点M从A点出发,绕侧面一周回到A点,求动点M轨迹长度的最小值.
图5 解析如图5所示,将三棱锥沿侧棱PA剪开摊平得到侧面展开图,易知∠APA′=120°,PA=PA′=a,线段AA′即为动点M轨迹长度最小值,易得AA′=3a,所以动点M轨迹长度最小 值为3a.
评注解决本题的关键是利用侧面展开图,这是求侧面上轨迹图形长度最值问题的最有效、最简便的方法,要训练学生牢固掌握这一方法.
例6已知圆台的上、下底面半径分别为2cm,4cm,AB是侧面上的母线,AB=6cm,一质点从点B绕侧面一周运动到A点,求质点运动轨迹的最小值.
图6解析如图6,把 圆台补成圆锥,沿母线SAB剪开摊平,侧面展开图如图所示,易知∠BSB′=2π3,线段BA′与AA′相交,设M为AA′上任一点,∠BSM=x,则∠A′SM=2π3-x,SA′=6,SB=12,y=BM+MA′=180-144cosx+6·(2π3-x),y′=144sinx2180-144cosx-6.
由y′=0得2sinx=5-4cosx,4cos2x-4cosx+1=0,cosx=12,x=π3,易知y在[0,π3] 递减,在[π3,2π3]递增,所以当x=π3时,ymin=63+2π.
易知,此时BM为AA′的切线,M为切点.
评注因为线段BA′ 与AA′ 弧相交,所以直接求线段BA′ 的长度是错误的,而这恰恰是很多学生所容易犯的错误.运动轨迹长度要想最小,质点必须从B点运动到AA′ 弧上一点M处,再从M点沿MA′ 弧运动到A′点.M点在AA′ 弧上的何处,需要通过列函数式求解.求解的结果可以看出,BM与AA′ 弧相切,这是一个很好的结论,值得体会.
3动点轨迹图形的面积
动点轨迹图形面积问题,一般是动直线所扫过的图形,求解关键是要弄清动点或动直线所扫过的轨迹图形的形状,这需要有一定的空间想象能力和逻辑推理能力.常见的轨迹图形主要是三角形、四边形、圆面、球面等.
例7在棱长为1的正方体ABCD-A1B1C1D1中,P、Q分别是线段AD1和B1C上的动点,且满足AP=B1Q,P、Q在運动过程中,求线段PQ在平面BCC1B1内的射影所形成的面积.
解析如图7,易知P点在平面BCC1B1内的射影P′ 落在线段BC1上,且BP′=AP=B1Q,所以P′Q∥BB1,图7所以PQ在运动过程中射影P′Q形成的轨迹图形为△OBB1和△OCC1,所以所求轨迹图形面积为S=12×1×1=12.
评注本题解决的关键是要弄清P、Q在运动过程中,线段PQ在平面BCC1B1内的射影图形是什么形状,从教学实践情况来看,学生对PQ在运动过程中射影P′Q满足P′Q∥BB1感到有一点困难.
例8已知正方体ABCD-A1B1C1D1的棱长为4,长为2的线段的两端点P、Q分别在棱DD1上和面ABCD内运动,求PQ中点M形成的轨迹图形的面积.
图8解析易知DD1⊥面ABCD,∠PDQ=90°所以DM=12PQ=1,
所以M点形成的轨迹图形是以D为球心,1为半径的18球面.
S=18×4π×12=π2.
评注解决这类问题要用到立体几何线面垂直的有关性质得出PD⊥DQ,再根据直角三角形斜边的中线等于斜边的一半,得出DM=1,从而得出M点形成的轨迹图形是以D为球心,1为半径的18球面,问题迎刃而解.
4动点轨迹图形的面积的最值
动点轨迹图形面积最值问题的求解,首先需要弄清动点或动直线所扫过的轨迹图形的形状,然后列出面积关系式,再根据有关的数学知识求得面积的最值.有些问题可直接根据几何图形的特点,得出面积的最值.
例9已知长方体ABCD—A1B1C1D1中,AB=AD=4,AA1=1,F为AD上的动点,且AF=λAD(0≤λ≤12),E为底面ABCD的中心,P为正方体表面上的动点,且满足A1P=xAF+yAE(x,y∈R),求动直线A1P所扫过的平面图形面积的最小值.
图9解析如图9所示,易知A1P所扫过平面图形为平行四边行A1FMG,建立空间直角坐标系, 易知A1(0,0,0),F(0,4λ,1),E(2,2,1)
a=A1F=(0,4λ,1),
b=AG=FM=2FE=2(2,2-4λ,0)
a·b=16λ-32λ2,a2=16λ2+1,b2=32(2λ2-2λ+1).
设a与b夹角为θ,则
S=a·b·sinθ=a·b·1-cos2θ
=a2·b2-(a·b)2
=(16λ2+1)·32·(2λ2-2λ+1)-(16λ-32λ2)2
=420λ2-4λ+2=420(λ-110)2+95
因为0≤λ≤12,所以当λ=110时,Smin=495=1255.
评注本题解决的关键是要弄清动直线A1P所扫过的平面图形的形状,而面积关系式则通过建立空间直角坐标系,利用空间向量的办法得出,这一方法对本题的求解显得比较巧妙,值得体会和总结.
5动点轨迹图形的体积或体积的最值
动点轨迹图形的体积或体积的最值问题,需要分析几何体的形状,恰当选择几何体的底面和高,使问题求解变得简便.
例10在棱长为1的正方体ABCD-A1B1C1D1中,P1、P2分别是线段AB和BD1上的动点,且不包括端点,在P1、P2运动过程中,图10线段P1P2始终平行于平面A1ADD1,求动点P1、P2和定点A、B1所形成的几何体P1P2AB1体积的最大值.
解析如图10,作P2O⊥平面ABB1A1,O为垂足,设AP1=x,则P1B=1-x,由△BP1P2∽△BAD1得P1P2AD1=P1BBA=1-x,由△OP1P2∽△A1AD1得OP2A1D1=P1P2AD1=1-x,所以OP2=(1-x)A1D1=1-x,VP2-P1AB1=13·S△P1AB1·OP2=13·12·x·1·(1-x)=16x(1-x)≤16·(x+1-x2)2=124.
等号成立的条件为x=1-x,即x=12.
评注解决本题的关键是要列出体积关系式.抓住动线段P1P2始终平行于平面A1ADD1这一条件,得出△OP1P2∽△A1AD1,从而找到相关线段的数量关系,再选择以P2为顶点,△P1AB1为底面,则容易列出体积关系式.根据体积关系式,不难求出体积的最大值.
例11已知正方形ABCD的边长为6,空间有一點M(不在平面ABCD内),满足MA+MB=10,求三棱锥M—ABC的体积的最大值.
解析由MA+MB=10知动点M的轨迹是以A、B为焦点的椭球面,椭圆的长半轴长a=5,短半轴长b=4,动点M到底面ABC距离的最大值为椭圆的短半轴长4,所以体积的最大值为
Vmax=13·12·6·6·4=24.
评注本题动点M的轨迹是根据椭圆定义得出的,体现了立体几何与解析几何交汇,是高考命题的新动向,也对考生的综合运用知识解决问题的能力提出了较高的要求.
立体几何中有关动点轨迹问题还有很多方面,它们往往比较新颖灵活,对空间想象能力和逻辑推理能力有较高要求,也需要有较强的创新意识.数学之魅力,体现在数学有很强的内在规律,教师要引导学生挖掘数学中所隐含的内在规律,使学生掌握研究数学的思想方法,理解数学的精髓,感悟数学的内在美,并在问题的解决中体验成功的快乐,激发探究的热情和动力,不断发展创造力.
作者简介吴成强(1963—),男,正高级教师,安徽省特级教师,安徽省池州市首届拔尖人才,池州市首批名师工作室主持人,池州市学科带头人,池州市优秀教师,十佳教师,安徽省教坛新星,安徽省先进工作者(省劳模),全国五一劳动奖章获得者,第十届苏步青数学教育奖获得者,2014年安徽省教育年度人物.在《中学数学杂志》等省级以上刊物发表学术论文70多篇,有两篇论文被中国人民大学书报资料中心《高中数学教与学》全文转载.

