基于碰撞作用的大跨径斜拉桥地震响应分析
.武芳文 孟园英 纪全有 杨源源

摘要:地震作用下,引桥与斜拉桥一旦发生碰撞,会增大斜拉桥的损伤风险。为了研究结构碰撞效应下大跨径斜拉桥主桥和引桥的地震响应问题,以1座典型半漂浮大跨径斜拉桥为例,采用Midas Civil大型有限元分析程序建立结构动力计算模型,基于动力时程分析法进行分析。结果表明:考虑单边碰撞时,主引桥基本周期接近时,碰撞力较小,单边碰撞会减小主桥梁端位移,增大引桥梁端和主塔塔顶位移,且单边碰撞效应大于双边碰撞,单边碰撞更大地影响与其相连的引桥。
关键词:大跨径斜拉桥;碰撞效应;双边碰撞;单边碰撞
中图分类号:U442.5+5 文献标识码:A 文章编号:1000-0666(2018)02-0337-05
0 引言
近年来大地震时有发生,很多桥梁结构遭受了不同程度的损坏,这导致部分交通系统的瘫痪,并增加了灾后救援的难度。目前,国内外众多学者对相邻梁体在伸缩缝处的碰撞效应进行了较为深入的研究。
在国外,Malhotra(1998)认为结构在受到碰撞效应与不考虑碰撞相比,桥梁结构的地震响应会减小;Reginald和Snsendar(2002)研究发现:双边碰撞时,刚度较小的框架结构位移会减小,而刚度较大的框架结构位移会增大,其内力在考虑碰撞之后也会按照刚度大小来进行分配;除此之外,Jankowski等(1998,2000)和Sang-Hyo(2000)对多跨简支梁桥由地震动空间变化引起的伸缩缝处相邻梁体间的碰撞效应进行了分析。
在国内,王斌斌和叶爱君(2010)采用非线性时程法分析了纵向碰撞对桥跨结构的整体反应,结果表明,碰撞对引桥的影响比较大;郭维和沈映红等(2002)分别进行了双边和单边碰撞反应研究,分析表明,双边碰撞发生时,较低桥墩的地震响应会增大,并发现碰撞响应主要影响因素为碰撞间隙和最大碰撞力。李建中和范立础等(2005)对临联之间的碰撞效应进行了研究。
对于地震作用下的碰撞研究,国内外学者针对简支梁桥或者小跨径连续梁桥的研究较多,而针对大跨径斜拉桥与引桥的碰撞效应的研究较少,且目前的研究结果并不完全一致(张文学等,2012,2013;薛成凤等,2017)。本文将斜拉桥与引桥简化为单边碰撞和双边碰撞模型,分别比较左引桥单边碰撞、右引桥单边碰撞和双边碰撞对桥梁结构的碰撞响应。
1 理论模型建立
研究地震作用下大跨径斜拉桥与引桥之间碰撞响应,首先应根据实桥资料,建立空间动力模型,正确选择与设计场地特征周期值相接近的地震波,准确模拟非线性边界与接触碰撞单元,再采用地震分析方法,进行有限元运算与分析。
本文以1座典型半漂浮大跨径斜拉桥为例研究斜拉桥伸缩缝处主、引桥梁体之间的碰撞对结构地震反应的影响规律。
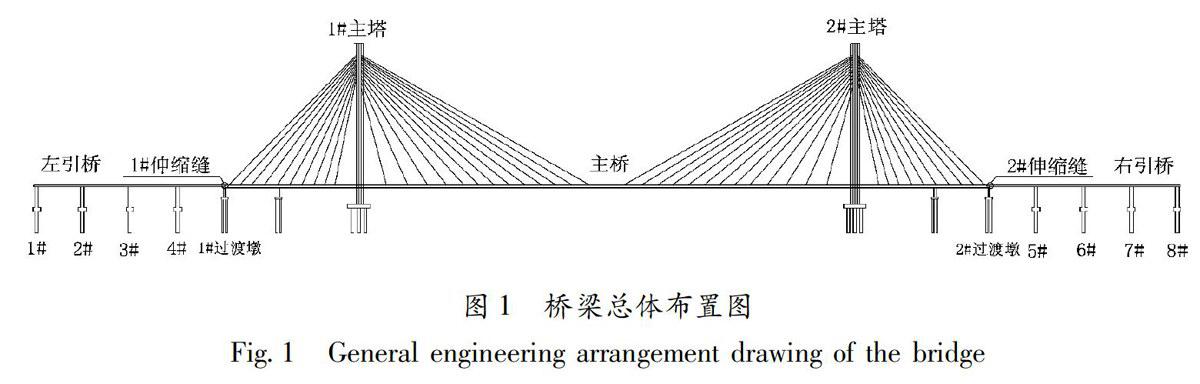
该斜拉桥桥跨采用对称结构,主桥采用双塔面漂浮体系斜拉桥,跨径的布置形式采用(45+67+416+67+45)m,主跨为钢箱梁,边跨为预应力混凝土箱梁,引桥为连续四跨,跨径为40m的预应力混凝土箱梁。为了分析主桥与引桥的碰撞对结构的地震反应,将主桥与引桥隔离开,主桥与引桥通过支座处的桥墩和伸缩缝处的间隙单元耦合起来。桥跨结构的总体布置如图1。
桩-土相互作用采用m 法进行计算,等代土弹簧刚度k,按照土介质的m值来计算,对桩侧抗计算时,根据桩基m法计算的基本原理,再结合桩长、桩径的值,合理设置弹簧的刚度,ks可表示为:式中:a为土弹簧所取代的土层厚度;bp为桩柱计算宽度,按照规范的有关规定取值:m为地基土比例系数,本文取40000kN/m4。
建立动力分析模型时,采用线弹性力一位移关系表示碰撞弹簧,不考虑碰撞过程中的能量损失,碰撞弹簧刚度k,取3.0×106kN/m(许祥等,2013;王东升,2004a,b;徐略勤,魏晓龙,2017),碰撞单元如图2所示。
2 结构动力计算模型及地震波输入
本文采用Midas Civil有限元程序建立结构动力分析模型,假设地震过程中主塔、桥墩始终处于弹性,不考虑桥墩的塑性变形,即主塔和桥墩均采用弹性的梁单元模拟;拉索采用仅受拉单元,并利用Ernst公式对斜拉索的垂度进行修正,如图3所示。
采用的地震记录加速度时程曲线应与场地抗震设防烈度相一致,桥梁位于Ⅶ度地震区,按照Ⅷ度设防,场地类别为Ⅱ类场地,水平方向设计地震动峰加速度为0.2g,地震动反应谱特征周期为0.40s。
选取表1所示的3条地震波,其加速度时程曲线如图4所示。为了与设计时的地震烈度相当,对选用的地震波加速度时程曲线按适当的比例(公式(2))调幅。调整后的加速度可表示为:
a1(t)=a(t)·A1max=a(t)·PGA/Amax(2)式中:PGA=Smax/2.25;a1(t)、A1max分别为调整后的加速度曲线和峰值;a(t),Amax分别为相对应的原记录值。
3 碰撞作用下桥梁地震响应分析
地震作用下,当邻梁相对位移大于伸缩缝的宽度时,碰撞即会在两相邻梁体之间发生,继而产生很大的脉冲力,很有可能导致局部的破坏,还有可能产生对桥墩和支座的破坏。
为了对比分析双边碰撞与单边碰撞对桥梁结构的影响,本文考虑以下3种工况:工况1:考虑双边碰撞;工况2:仅考虑左引桥与主桥碰撞情况下的单边碰撞;工况3:仅考虑右引桥与主桥碰撞情况下的单边碰撞。
为了更简明地表达碰撞对桥梁结构的影响,引入位移峰值比Dp/Dn,剪力峰值比Fp/Fn,弯矩峰值比Mp/Mn,其中p表示考慮单边碰撞时的效应,n表示考虑双边碰撞时的效应。
3.1 伸缩缝碰撞力的结果
图5给出了单边碰撞相比双边碰撞下1#缝和2#缝处碰撞力峰值比及其对应的时程曲线图。图中可以看出,单边碰撞与双边碰撞时间基本一致,不同地震波单边碰撞与双边碰撞在伸缩缝处的碰撞力不大一致,Chi-Chi地震波在单边碰撞下伸缩缝处的碰撞力均大于双边碰撞,汶川地震波和雅安地震波在引桥墩高为20m时,单边碰撞下碰撞力均小于双边碰撞下,最小达到双边碰撞力的0.47倍和0.72倍,即减小了53%和28%,在引桥墩高小于15m和大于25m时,单边碰撞下的碰撞力大于双边碰撞下产生的碰撞力。对于不同引桥墩高,双边碰撞与单边碰撞均要单独考虑,碰撞效应不可忽视。
3.2 桥墩位移及内力响应
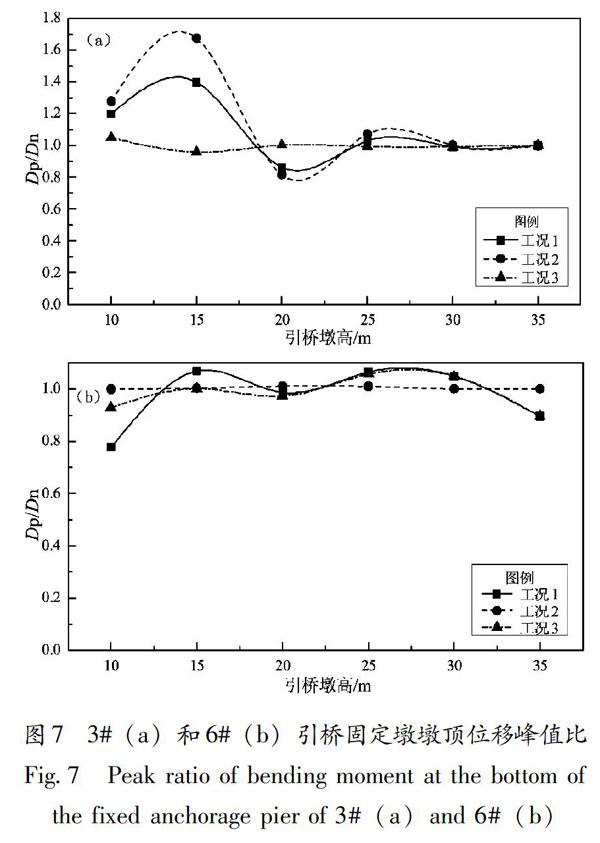
图6~7给出引桥固定墩墩底弯矩和墩顶位移峰值比,从图中可以看出:碰撞对引桥固定墩墩底弯矩和墩顶位移影响趋势一致,仅考虑左引桥单边碰撞和双边碰撞对3#固定墩墩底弯矩和墩顶位移影响比较大,在引桥墩高小于15m时,碰撞会增大,3#固定墩墩底弯矩和墩顶位移最大增大72%,仅考虑右引桥单边碰撞和双边碰撞对6#固定墩底弯矩和墩顶位移影响比较大,在引桥墩高为5m时,碰撞会减小6#固定墩底弯矩和墩顶位移,双边碰撞比仅考虑右引桥单边碰撞影响大,最大减小25%。
因此,在引桥墩高小于20m时,双边碰撞和仅考虑左引桥单边碰撞对3#固定墩的影响比较大,且仅考虑左引桥单边碰撞对3#固定墩的影响大于双边碰撞效应,双边碰撞和仅考虑右引桥单边碰撞对6#固定墩的影响比较大。
4 结论
本文以1座典型半漂浮大跨径斜拉桥为例,研究在不同地震作用下,斜拉桥与引桥之间的碰撞效应,结果表明:
(1)不同地震波作用下结构的地震效应有所不同,由于大跨径斜拉桥与两边引桥的结构形式有很大差别,结构动力特性也有很大差别,两伸缩缝的碰撞情况不仅受地震波频谱特性和结构动力特性的影响,两边碰撞情况也相互影响。
(2)仅考虑單边碰撞时,若引桥基本周期与主桥基本周期接近时,单边碰撞会减小伸缩缝处的碰撞力;碰撞更大的影响与其相连的引桥梁位移值,且单边碰撞影响比双边碰撞大;双边碰撞对引桥固定墩墩底剪力影响不大,单边碰撞对其相连接引桥固定墩墩底弯矩和墩顶位移影响比较大;从碰撞作用下结构的地震特性可以得出,采用引桥周期与主桥周期较接近的邻联桥跨结构对结构的抗震比较有利。
参考文献:
郭维,沈映红.2002.高架简支梁桥非线性碰撞地震反应分析[J].地震工程与工程振动,22(4):108-113.
李建中,范立础.2005.非规则梁桥纵向地震反应及碰撞效应[J].土木工程学报,13(1):84-90.
王斌斌,叶爱君.2010.地震作用下大跨度斜拉桥和引桥间碰撞分析[J].振动与冲击,29(3):95-99.
王东升,冯启民,王国新,等.2004a.基于直杆共轴碰撞理论的桥梁地震反应邻梁碰撞分析模型[J].工程力学,21(2):157-166.
王东升,王国新,冯启民,等.2004b.桥梁结构地震反应邻梁碰撞分析等效刚体模型[J].工程力学,21(2):81-85.
徐略勤,魏晓龙.2017.地震作用下双薄壁高墩刚构桥桥台处的碰撞效应及减碰措施[J].地震工程学报,39(3):425-433.
许祥,鞠三,刘伟庆,等.2013.桥梁结构地震碰撞分析模型的碰撞刚度计算方法研究[J].振动与冲击,32(12):31-39.
薛成凤,刘来君,武芳文.2017.大跨度混凝土斜拉桥横向地震作用易损性分析[J].地震研究,40(1):64-69.
杨草方.2016.考虑碰撞作用的大跨斜拉桥地震响应分析[D].西安:长安大学.
张文学,鲍艳,王景景.2012伸缩缝间隙及纵向阻尼器对斜拉桥的碰撞影响[J].公路交通科技,29(8):60-63.
张文学,昊海军,陈士通,等.2013.橡胶缓冲装置对斜拉桥及引桥碰撞影响研究[J].振动与冲击,32(7):151-154.
Jankowski R,Wilde K,Eujino Y.1998.Pounding of superstructure in ele-vated bridge during earthquakes[J].Earthquake Engineering andStructural Dynamics,27(5):487-502.
Jankowski R,Wilde K,Fujino Y.2000.Reduction of pounding effects inelevated bridges during earthquakes[J].Earthquake Engineeringand Structural Dynamics,29(2):195-212.
Malhotra P K.1998.Dynamics of seismic pounding at expansion joints ofconcrete bridges[J].Journal of Engineering Mechanics,124(7):794-802.
Reginald D,Susendar M.2002.Effect of pounding and restrainers on seis-mic response of multipule 2 frame bridges[J].Journal of StructuralEngineering,128 (7):860-869.
Sang-Hyo K,Sang-Woo L,Jeong-Hun W,et al.2000.Dynamic behaviorsof bridges under seismic excitations with pounding between adjacentgirders.[J].Earthquake Engineering and Structural Dynamics,26(2):1815.



摘要:地震作用下,引桥与斜拉桥一旦发生碰撞,会增大斜拉桥的损伤风险。为了研究结构碰撞效应下大跨径斜拉桥主桥和引桥的地震响应问题,以1座典型半漂浮大跨径斜拉桥为例,采用Midas Civil大型有限元分析程序建立结构动力计算模型,基于动力时程分析法进行分析。结果表明:考虑单边碰撞时,主引桥基本周期接近时,碰撞力较小,单边碰撞会减小主桥梁端位移,增大引桥梁端和主塔塔顶位移,且单边碰撞效应大于双边碰撞,单边碰撞更大地影响与其相连的引桥。
关键词:大跨径斜拉桥;碰撞效应;双边碰撞;单边碰撞
中图分类号:U442.5+5 文献标识码:A 文章编号:1000-0666(2018)02-0337-05
0 引言
近年来大地震时有发生,很多桥梁结构遭受了不同程度的损坏,这导致部分交通系统的瘫痪,并增加了灾后救援的难度。目前,国内外众多学者对相邻梁体在伸缩缝处的碰撞效应进行了较为深入的研究。
在国外,Malhotra(1998)认为结构在受到碰撞效应与不考虑碰撞相比,桥梁结构的地震响应会减小;Reginald和Snsendar(2002)研究发现:双边碰撞时,刚度较小的框架结构位移会减小,而刚度较大的框架结构位移会增大,其内力在考虑碰撞之后也会按照刚度大小来进行分配;除此之外,Jankowski等(1998,2000)和Sang-Hyo(2000)对多跨简支梁桥由地震动空间变化引起的伸缩缝处相邻梁体间的碰撞效应进行了分析。
在国内,王斌斌和叶爱君(2010)采用非线性时程法分析了纵向碰撞对桥跨结构的整体反应,结果表明,碰撞对引桥的影响比较大;郭维和沈映红等(2002)分别进行了双边和单边碰撞反应研究,分析表明,双边碰撞发生时,较低桥墩的地震响应会增大,并发现碰撞响应主要影响因素为碰撞间隙和最大碰撞力。李建中和范立础等(2005)对临联之间的碰撞效应进行了研究。
对于地震作用下的碰撞研究,国内外学者针对简支梁桥或者小跨径连续梁桥的研究较多,而针对大跨径斜拉桥与引桥的碰撞效应的研究较少,且目前的研究结果并不完全一致(张文学等,2012,2013;薛成凤等,2017)。本文将斜拉桥与引桥简化为单边碰撞和双边碰撞模型,分别比较左引桥单边碰撞、右引桥单边碰撞和双边碰撞对桥梁结构的碰撞响应。
1 理论模型建立
研究地震作用下大跨径斜拉桥与引桥之间碰撞响应,首先应根据实桥资料,建立空间动力模型,正确选择与设计场地特征周期值相接近的地震波,准确模拟非线性边界与接触碰撞单元,再采用地震分析方法,进行有限元运算与分析。
本文以1座典型半漂浮大跨径斜拉桥为例研究斜拉桥伸缩缝处主、引桥梁体之间的碰撞对结构地震反应的影响规律。
该斜拉桥桥跨采用对称结构,主桥采用双塔面漂浮体系斜拉桥,跨径的布置形式采用(45+67+416+67+45)m,主跨为钢箱梁,边跨为预应力混凝土箱梁,引桥为连续四跨,跨径为40m的预应力混凝土箱梁。为了分析主桥与引桥的碰撞对结构的地震反应,将主桥与引桥隔离开,主桥与引桥通过支座处的桥墩和伸缩缝处的间隙单元耦合起来。桥跨结构的总体布置如图1。
桩-土相互作用采用m 法进行计算,等代土弹簧刚度k,按照土介质的m值来计算,对桩侧抗计算时,根据桩基m法计算的基本原理,再结合桩长、桩径的值,合理设置弹簧的刚度,ks可表示为:式中:a为土弹簧所取代的土层厚度;bp为桩柱计算宽度,按照规范的有关规定取值:m为地基土比例系数,本文取40000kN/m4。
建立动力分析模型时,采用线弹性力一位移关系表示碰撞弹簧,不考虑碰撞过程中的能量损失,碰撞弹簧刚度k,取3.0×106kN/m(许祥等,2013;王东升,2004a,b;徐略勤,魏晓龙,2017),碰撞单元如图2所示。
2 结构动力计算模型及地震波输入
本文采用Midas Civil有限元程序建立结构动力分析模型,假设地震过程中主塔、桥墩始终处于弹性,不考虑桥墩的塑性变形,即主塔和桥墩均采用弹性的梁单元模拟;拉索采用仅受拉单元,并利用Ernst公式对斜拉索的垂度进行修正,如图3所示。
采用的地震记录加速度时程曲线应与场地抗震设防烈度相一致,桥梁位于Ⅶ度地震区,按照Ⅷ度设防,场地类别为Ⅱ类场地,水平方向设计地震动峰加速度为0.2g,地震动反应谱特征周期为0.40s。
选取表1所示的3条地震波,其加速度时程曲线如图4所示。为了与设计时的地震烈度相当,对选用的地震波加速度时程曲线按适当的比例(公式(2))调幅。调整后的加速度可表示为:
a1(t)=a(t)·A1max=a(t)·PGA/Amax(2)式中:PGA=Smax/2.25;a1(t)、A1max分别为调整后的加速度曲线和峰值;a(t),Amax分别为相对应的原记录值。
3 碰撞作用下桥梁地震响应分析
地震作用下,当邻梁相对位移大于伸缩缝的宽度时,碰撞即会在两相邻梁体之间发生,继而产生很大的脉冲力,很有可能导致局部的破坏,还有可能产生对桥墩和支座的破坏。
为了对比分析双边碰撞与单边碰撞对桥梁结构的影响,本文考虑以下3种工况:工况1:考虑双边碰撞;工况2:仅考虑左引桥与主桥碰撞情况下的单边碰撞;工况3:仅考虑右引桥与主桥碰撞情况下的单边碰撞。
为了更简明地表达碰撞对桥梁结构的影响,引入位移峰值比Dp/Dn,剪力峰值比Fp/Fn,弯矩峰值比Mp/Mn,其中p表示考慮单边碰撞时的效应,n表示考虑双边碰撞时的效应。
3.1 伸缩缝碰撞力的结果
图5给出了单边碰撞相比双边碰撞下1#缝和2#缝处碰撞力峰值比及其对应的时程曲线图。图中可以看出,单边碰撞与双边碰撞时间基本一致,不同地震波单边碰撞与双边碰撞在伸缩缝处的碰撞力不大一致,Chi-Chi地震波在单边碰撞下伸缩缝处的碰撞力均大于双边碰撞,汶川地震波和雅安地震波在引桥墩高为20m时,单边碰撞下碰撞力均小于双边碰撞下,最小达到双边碰撞力的0.47倍和0.72倍,即减小了53%和28%,在引桥墩高小于15m和大于25m时,单边碰撞下的碰撞力大于双边碰撞下产生的碰撞力。对于不同引桥墩高,双边碰撞与单边碰撞均要单独考虑,碰撞效应不可忽视。
3.2 桥墩位移及内力响应
图6~7给出引桥固定墩墩底弯矩和墩顶位移峰值比,从图中可以看出:碰撞对引桥固定墩墩底弯矩和墩顶位移影响趋势一致,仅考虑左引桥单边碰撞和双边碰撞对3#固定墩墩底弯矩和墩顶位移影响比较大,在引桥墩高小于15m时,碰撞会增大,3#固定墩墩底弯矩和墩顶位移最大增大72%,仅考虑右引桥单边碰撞和双边碰撞对6#固定墩底弯矩和墩顶位移影响比较大,在引桥墩高为5m时,碰撞会减小6#固定墩底弯矩和墩顶位移,双边碰撞比仅考虑右引桥单边碰撞影响大,最大减小25%。
因此,在引桥墩高小于20m时,双边碰撞和仅考虑左引桥单边碰撞对3#固定墩的影响比较大,且仅考虑左引桥单边碰撞对3#固定墩的影响大于双边碰撞效应,双边碰撞和仅考虑右引桥单边碰撞对6#固定墩的影响比较大。
4 结论
本文以1座典型半漂浮大跨径斜拉桥为例,研究在不同地震作用下,斜拉桥与引桥之间的碰撞效应,结果表明:
(1)不同地震波作用下结构的地震效应有所不同,由于大跨径斜拉桥与两边引桥的结构形式有很大差别,结构动力特性也有很大差别,两伸缩缝的碰撞情况不仅受地震波频谱特性和结构动力特性的影响,两边碰撞情况也相互影响。
(2)仅考虑單边碰撞时,若引桥基本周期与主桥基本周期接近时,单边碰撞会减小伸缩缝处的碰撞力;碰撞更大的影响与其相连的引桥梁位移值,且单边碰撞影响比双边碰撞大;双边碰撞对引桥固定墩墩底剪力影响不大,单边碰撞对其相连接引桥固定墩墩底弯矩和墩顶位移影响比较大;从碰撞作用下结构的地震特性可以得出,采用引桥周期与主桥周期较接近的邻联桥跨结构对结构的抗震比较有利。
参考文献:
郭维,沈映红.2002.高架简支梁桥非线性碰撞地震反应分析[J].地震工程与工程振动,22(4):108-113.
李建中,范立础.2005.非规则梁桥纵向地震反应及碰撞效应[J].土木工程学报,13(1):84-90.
王斌斌,叶爱君.2010.地震作用下大跨度斜拉桥和引桥间碰撞分析[J].振动与冲击,29(3):95-99.
王东升,冯启民,王国新,等.2004a.基于直杆共轴碰撞理论的桥梁地震反应邻梁碰撞分析模型[J].工程力学,21(2):157-166.
王东升,王国新,冯启民,等.2004b.桥梁结构地震反应邻梁碰撞分析等效刚体模型[J].工程力学,21(2):81-85.
徐略勤,魏晓龙.2017.地震作用下双薄壁高墩刚构桥桥台处的碰撞效应及减碰措施[J].地震工程学报,39(3):425-433.
许祥,鞠三,刘伟庆,等.2013.桥梁结构地震碰撞分析模型的碰撞刚度计算方法研究[J].振动与冲击,32(12):31-39.
薛成凤,刘来君,武芳文.2017.大跨度混凝土斜拉桥横向地震作用易损性分析[J].地震研究,40(1):64-69.
杨草方.2016.考虑碰撞作用的大跨斜拉桥地震响应分析[D].西安:长安大学.
张文学,鲍艳,王景景.2012伸缩缝间隙及纵向阻尼器对斜拉桥的碰撞影响[J].公路交通科技,29(8):60-63.
张文学,昊海军,陈士通,等.2013.橡胶缓冲装置对斜拉桥及引桥碰撞影响研究[J].振动与冲击,32(7):151-154.
Jankowski R,Wilde K,Eujino Y.1998.Pounding of superstructure in ele-vated bridge during earthquakes[J].Earthquake Engineering andStructural Dynamics,27(5):487-502.
Jankowski R,Wilde K,Fujino Y.2000.Reduction of pounding effects inelevated bridges during earthquakes[J].Earthquake Engineeringand Structural Dynamics,29(2):195-212.
Malhotra P K.1998.Dynamics of seismic pounding at expansion joints ofconcrete bridges[J].Journal of Engineering Mechanics,124(7):794-802.
Reginald D,Susendar M.2002.Effect of pounding and restrainers on seis-mic response of multipule 2 frame bridges[J].Journal of StructuralEngineering,128 (7):860-869.
Sang-Hyo K,Sang-Woo L,Jeong-Hun W,et al.2000.Dynamic behaviorsof bridges under seismic excitations with pounding between adjacentgirders.[J].Earthquake Engineering and Structural Dynamics,26(2):1815.

