苏龙霞
【摘要】在小学数学课堂教学中,实验操作成为一种常态,惟有探索性的实验操作才是必要而有价值的,才能促进真正深度学习的产生。以人教版五年级“可能性”的教学为例,探索论证了怎样的实验才是必要而有价值的,怎样的实验才能促进深度学习的产生。
【关键词】探索性实验 验证性实验 深度学习
一、背景
在一次市个人专场的教学现场中,选择执教人教版五年级的“可能性”,“可能性”的学习属于概率的领域,在2011版人教版小学阶段唯一安排在第二学段的一次学习。不管哪个版本在哪个学年执教“可能性”时,所有老师都无一例外地组织学生进行实验活动,或摸球或摸牌、摸棋,那么在摸球摸牌摸棋实验中怎么样的实验才是有价值而必要的呢?怎样的实验才能促进深度学习的产生呢?
二、教材比较
2011版的教材对于概率的学习,只安排五年级上册3个例题与配套的一个练习以及一个实践活动。例1是在表演节目的活动中,引出了可能、一定、不可能三种情况,然后再对确定现象和随机现象的三种具体结果,进行进一步分析。例2是摸棋子活动:知道盒中红、蓝棋子各有多少(红4蓝1),摸20次,统计摸出红、蓝棋子的次数,得出结果“摸出红棋子的可能性大”。例3是重复20次摸红黄两种颜色混合的球(球的总数未知),从摸的结果猜红球多还是黄球多?
而翻看2001版人教版的教材安排,则安排了3次的学习,分别在三年级上册例1到例5,以及五年级上册例1到例3,共8个例题3个章节的学习,教材的内容从感知可能性的存在、大小到应用解决现实问题等。
可以看出,2个版本的教材侧重各不一样:
1.教材导入的重心是不一样的。2001版的教材将重心放在了“一定”和“不可能”两个确定现象上,而2011版的教材着重将引入的点和讨论的范围放到了可能这一情况上。
2.对实验频率和理论频率存在偏差的安排不一样。2001版没有专门的章节学习其偏差的不一样,而2011版的则凸显了偏差的学习,不仅有新授例题还有对应习题的学习。
3.对可能性大小刻画方法的学习安排不一样。2001版中不仅有等可能性的学习,还有初步可能性大小的计算(理论概率),而2011版的教材则只要求此年段学生,对随机事件和等可能事件有一定了解即可,所以放到了数学活动课(实践活动“掷一掷”)中。
三、教材思考
教材为什么做这样的修改?(实验版和修订版)人教版小学唯一一次学习概率的安排,其用意是什么?
应该说是不仅考虑到五年级学生的认知积累,更重要的是对概率思想的一个启蒙,初步体会随机事件无所不在,但观察其频率,仍有一定的规律可寻。
(一)教学尝试——一磨,验证性的实验
1.实验器材:扑克牌(4红1黑)。
2.实验规则:每次摸完牌放入重新洗牌再摸,小组合作,每人4次,记录摸牌情况。
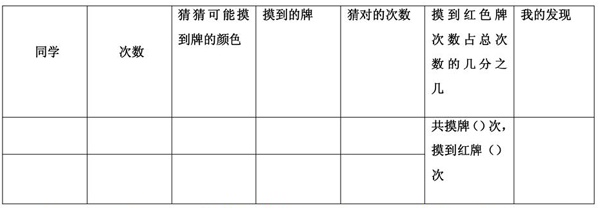
3.实验记录单。
4.现场呈现。当摸到第三次时,随机喊停,问:已经连续摸到3次红色牌,接下去一定摸到黑色牌吗?为什么?(生:当然不会一定是黑色的牌,既有可能红色也有可能黑色牌)
捕捉:每个小组同学在摸牌过程中都不由自主的分成2个方阵,只要一方说一个颜色(红或黑)牌,另一方就反之说相反颜色(黑或红)的牌,每个小组5个同学,到最后已經有同学没有兴趣再猜了。(为什么?答:不是红就是黑呀,红色的多几次那就黑的吧,反正八九不离十……)
5.发现结论。每次摸牌都有2种可能性;按道理摸到红牌的几率(用上了几率)更大些,可是实际摸牌却不是这样;不用再摸牌了,结论不一定。
(二)课后思考:什么样的实验才是必要而有价值的?怎样的实验才能促进真正深度学习的产生
1.学生有实验的需求与必要吗?学生已经直观知道了(4红1黑的扑克牌)摸到红色牌比摸到黑色牌的可能性比较大,甚至有的孩子已经大概了解其摸到红色牌的概率(理论概率)为4/5,再让孩子重复实验20次,而得到的结果也仅仅是——摸到红色牌的可能性更大?可在实际的实验操作中,却得不到我们想要的结果,在摸牌20次当中,摸到红牌的次数分别是7次、12次、6次、14次、10次,即使把各小组摸到红牌的次数加起来也不能很好验证其最初的猜测,学生越摸牌对一开始的直觉概率越模糊了。实验的主体是谁?学生在其中该充当怎样的角色呢?为什么学生对这次实验没有兴趣?
2.学生是作推理性的实验还是验证性的实验?“如果要做验证,几千次都不够;如果要做推断,60次就足够。”(《统计数字会撒谎》)那么,我们在实验中是让学生作“操作工”还是“探究者”,是归纳思维还是演绎思维?实践告诉我们,只有“大数定律一般能保证‘频率趋向于概率”,可是课堂上只有20次的实验显然满足不了大数的要求,而且大数的复杂性似乎小学生也难以把握。
3.怎样的数据才是有效的?在摸牌20次当中,摸到红牌的次数分别是7次、12次、6次、14次、10次,这些数据有效吗?怎么去体现关于数据分析观念,2011版《课标》指出,应“了解在现实生活中,有许多问题应当先做调查研究,搜集数据,通过分析做出判断”。学生通过摸牌得到的数据显然没办法验证之前的猜测之前的直觉概率思维,为什么有学生对概率对可能性却似乎搞晕了?
(三)授课现场——探索性的实验
1.实验器材:8袋球(5红1黑,5黑1红;各4袋,除了颜色其他都一样),告诉孩子球的总数及有2种颜色但不告诉各颜色球的数量。
2.实验规则:每次摸出一个球,记录员用正字法记录结果;每次摸完球放回重新摇晃再摸;每个同学摸5次,第一个同学摸后完,小组做好第一次统计及预测;小组全部结束后,要做好第二次统计与预测。
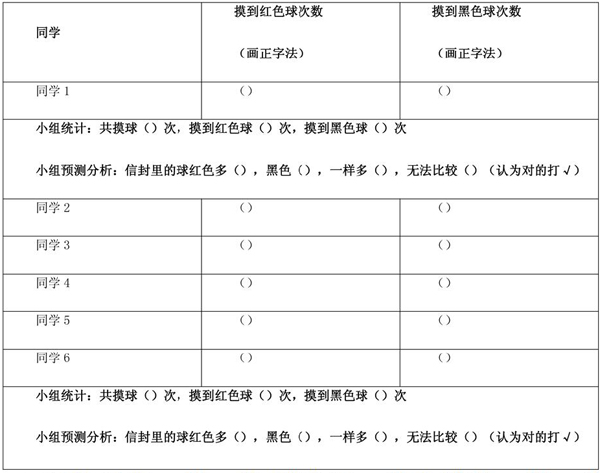
3.实验记录单:
4.现场呈现:第一次摸球完,学生辨论:第一次摸球,能马上判断出球的组成吗?第二次?第三次……还要继续摸球吗?(要)整个小组按规定摸完球,讨论:比较第一次和第二次统计与猜测,你们有什么发现?能否猜猜袋子中大概有几个红球几个黑球?
捕捉:学生跃跃欲试,每次猜球充满挑战性。小组同学球摸完了,还想再摸再猜,并且急于想知道真正的结果。
5.发现结论:每次摸球都充满随机性,无法准确判断是什么或什么;随着摸球次数的增多,才有一点点规律,红球多或者黑球多;有必要继续摸球下去,结果会更准确。
6.延伸。猜猜:哪2组的球是一样的,为什么这样猜测?比如,第一组球(5红1黑)中,若规定摸到红色球为女生赢,摸到黑色球为男生赢,那么女生一定赢吗?为什么?怎么解释女生赢得可能性更大?对可能性有什么新的发现?
(四)案例启示
1.探索性的实验促使深度学习的产生,有助于创新意识创新精神的培养。
探究性实验是有意识探索未知的实验,是在教师的引导下,先通过组织实验观察活动,然后对比分析实验中产生现象、数据,探究其因果关系,形成某种结论,发现某种规律。这种实验的研究方法可以很好培养学生的观察能力、思维能力、探索精神、良好的学习方法,而这些就是深度学习的必须是创新精神的基础。
验证性实验是指对研究对象有了一定了解,并形成了一定认识或提出了某种假说,为验证这种认识或假说是否正确而进行的一种实验。验证性实验强调演示和证明科学内容的活动,科学知识和科学过程分离。
实践早已表明,探索性实验作为学生的一种积极主动的认识建构手段,让学生接触探索、发明、发现的过程和方法。本课例在作课过程中所运用的就是探索性的实验,在探索发现的过程中,发展学生理性的、批判的思想方法,体验研究的苦衷和愉悦,培养他们的发现、探究能力,不断实现创新的培养。
2.探索性实验对学习概率(可能性)是必要而有价值的。
在第一次磨课上课中,学生当看到牌(4红1黑)时,就有直觉概率思维是摸到红牌的可能性比较大,甚至有的已经说摸到红牌的可能性为4/5,这时再组织学生进行实验——是否摸到红牌的可能性更大或者其为4/5,经过有限次的摸牌,学生思维反而模糊了。因为摸牌的结果不确定(在摸牌20次当中,摸到红牌的次数分别是7次、12次、6次、14次、10次),即使把各小组摸到紅牌的次数加起来也不能很好验证其最初的猜测,学生越摸牌对一开始的直觉概率(4/5)似乎越模糊了。
而在个人专场执教时,学生在不知道球(或牌)组成的前提下进行摸球,显然地,他们逐步体会到,摸一次不行,2次、3次……随着摸球次数的增多,在数据的比较思考中,才逐步有了自己的猜测,再次摸球成为必要的活动,在猜测及最后的对照中得出自己的摸球数据的可考性,其活动积极性和参与感极强。
实践证明,要保证“频率(几率)趋向于概率”就必须要大数原则,而课堂上几次学生的摸球活动(小组20次,全班共160次)显然体现不了“大数”,也就不能验证所需要的结论了。达莱尔·哈夫(美国统计专家)在《统计数字会撒谎》一书中就明确指出,“如果要做验证,几千次都不够;如果要做推断(探索),60次就足够。”华东师大教授张奠宙在《小学数学教材中的大道理》同样指出,大数原则对于小学生的要求太高了。
3.探索性实验促进基本活动
经验的有效积累。
2011版《课程标准》告诉我们,设计有效的数学探索活动是学生积累活动经验的保障,必须引导学生“经历在实际问题探索中发现、收集和处理数据,并利用生成数据发现问题、分析问题,从而掌握统计与概率的基础知识和基本技能”。课标修订组组长史宁中在《小学数学教学策略》一书这样说,“需要指出的是,我们赞成做实验,赞成运用统计的思想来做实验”。统计是通过数据来获取一些信息,来帮助人们做出一些判断。他举例说,“同样是一个袋子里有5个球、4个白球、1个红球,如如果让学生通过摸来验证出现白球的可能性是4/5,出现红球的可能性1/5,这不是统计。统计这样的,告诉学生们袋子里有很多球,有白颜色的和红颜色的。让孩子们去摸,摸到一定程度的时候,学生发现摸出白球的次数比红球的次数多,由此推断袋子里白球可能比红球多。进一步的话,能推断出出白球和红球的比例大概是多少。再告诉球的总数的时候,能够估计出来几个白球和几个红球,这个才是统计的过程,这才是有效经验的积累”。
参考文献:
[1]达莱尔·哈夫.统计数字会撒谎[D].北京:中国城市出版社,2009.3.
[2]中华人民共和国教育部制定.义务教育语文课程标准[M].北京:北京师范大学出版社,2012.
[3]张丹.小学数学教学策略[D].北京:北京师范大学出版社,2010.8
- 无创正压通气对COPD合并呼吸衰竭者的疗效分析
- 脑梗塞患者血清同型半胱氨酸、超敏C反应蛋白、血脂检测结果分析
- 甲状腺癌超声诊断与病理诊断对比分析和研究
- 慢性乙型病毒性肝炎疾病相关治疗分析
- 健康体检者血脂及血尿酸水平同糖尿病发生的相关性分析
- 鼻内镜手术在慢性鼻窦炎患者治疗中的应用效果观察
- 聚焦解决模式在学龄前儿童膳食营养和睡眠干预中的应用效果分析
- MRI与CT对新生儿缺氧缺血性脑病的诊断效果比较
- 预成纤维桩或可塑纤维桩用于口腔修复的有效性分析
- 卵巢卵泡膜-纤维瘤组肿瘤超声检查与诊断价值分析
- 孕期保健对高龄产妇并发症及妊娠结局的影响分析
- 腹腔镜胆囊切除术与开腹手术治疗胆结石的临床疗效分析
- 应激对2型糖尿病患者神经内分泌相关激素的影响
- 浅谈实验室药品微生物检验质量把控影响因素
- 中西医结合治疗宫内节育器致子宫异常出血的临床分析
- 静脉麻醉在消化内镜微创治疗中的临床应用分析
- 应用微创穿刺引流术治疗高血压性基底节区脑出血的临床效果分析
- 中空加压螺丝钉治疗新鲜股骨颈骨折效果探究
- 输血性疟病例的实验室检测及调查研究
- 白内障超声乳化联合机械性房角分离治疗闭角型青光眼效果观察
- 全数字胃肠造影检查的临床应用分析
- 急诊和延期腹腔镜手术治疗急性胆囊炎的临床疗效分析
- 早期综合康复治疗急性脑血栓脑梗患者的临床效果观察
- 腹腔镜与宫腔镜手术治疗不同体积Ⅱ型子宫肌瘤的价值分析
- 老年脑外伤扩大去骨瓣减压术后硬膜下积液的临床治疗研究
- smiler
- smilers
- smiles
- smilet
- smiley
- smileyer
- smileyest
- smiley face
- smileys
- smile²
- smile¹
- smiling
- smirk
- smirked
- smirker
- smirkers
- smirking
- smirkingly
- smirks
- smithereens
- smitten
- smock
- smocked
- smocker
- smockless
- 小说的人物与情节
- 小说的人物出场
- 小说的人物命名
- 小说的人物塑造
- 小说的人物对话
- 小说的人物性格
- 小说的人物转变
- 小说的伏笔
- 小说的入话
- 小说的关键在于个别
- 小说的剪裁
- 小说的动作描写
- 小说的叙述
- 小说的含蓄
- 小说的呼语
- 小说的场面
- 小说的声部
- 小说的复合美
- 小说的幽默
- 小说的序幕
- 小说的开头
- 小说的引子
- 小说的引言
- 小说的总体构思
- 小说的情势