《让数学概念在模型思想中生长》-理学论文，数学论文-论文范文参考-科学狗论文网

标题

让数学概念在模型思想中生长

范文

徐瑞

【摘要】数学概念是客观现实中的数量关系和空间形式的本质属性在人脑中的反映.数学的研究对象是客观事物的数量关系和空间形式，也就是说要想学好数学首先要弄清数学概念.2011版《新课程标准》指出：在数学课程中应当注重发展学生的模型思想.模型思想在概念教学中的体现就是要从现实生活或具体情境中抽象出数学问题，或把抽象的概念利用模型思想与现实生活或具体情境建立联系，形成模型，从而提高学生学习数学的兴趣和应用数学的意识.

【关键词】数学概念;模型思想;提高效率

2011版《新课程标準》指出：在数学课程中应当注重发展学生数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力和模型思想.其中，模型思想的建立是学生体会和理解数学与外部世界联系的基本途径，建立和求解模型的过程包括：从现实生活或具体情境中抽象出数学问题，或把抽象的概念利用模型思想与现实生活或具体情境建立联系，这些内容的学习有助于学生初步形成模型思想，提高学习数学的兴趣和应用意识.

数学概念是客观现实中的数量关系和空间形式的本质属性在人脑中的反映.数学的研究对象是客观事物的数量关系和空间形式，也就是说要想学好数学首先要弄清数学概念.小学数学中有很多概念，包括数的概念、运算的概念、量与计量的概念、几何形体的概念、比和比例的概念、方程的概念，以及统计初步知识的有关概念等.这些概念是构成小学数学基础知识的重要内容，它们是互相联系着的.只有明确、牢固地掌握数的概念，才能理解运算概念，而运算概念的掌握，又能促进数的整除性概念的形成.那么，如何才能在小学数学概念教学中运用模型思想，把抽象、乏味的数学概念与生活实际或具体情境建立联系，从而减小学生的学习难度，提高学生的学习兴趣，提升教师的教学效率呢？

一、巧设情境，建立数学与生活的联系

概念教学是以学生学习、探讨客观世界数量关系和空间形式的本质属性为宗旨的课堂教学.小学数学概念是小学数学学习的重要基础知识，是数学学习的核心，学生只有正确理解和掌握数学概念才能有效地进行数学学习.对抽象概念的教学要弄清概念的本质，只有弄清本质才能在生活中找出其原型并帮助学生建立概念模型，从而达到理解和掌握概念的目的.

例如，教授减法的性质a-b-c=a-（b+c）时，教师通常的做法是让学生通过计算几组a-b-c式的题目与几组a-（b+c）式的题目，通过比较发现结果相等，从而推导出a-b-c=a-（b+c），学生鉴于当时的临时记忆似乎也能明白，之后通过大量的练习巩固，好像也会应用.但一旦在简便计算中出现a-b+c或a-（b-c）题型时，学生的错误随之产生，所有的问题一下子就完全暴露出来了.究其原因就是因为学生对减法的性质的本质没有完全理解，头脑中没有相应的模型，从而产生混乱并出现错误.

鉴于此，笔者设计了如下的教学环节：快要开学了，小明的妈妈带了100元钱去商店准备给小明买一支钢笔和一个书包，已知钢笔每支22元，书包每个48元，买完东西后妈妈还剩多少元钱？学生自然会想到100-22-48和100-（22+48）两种方法.这时教师适时追问：这两种方法都可以吗？它们的运算顺序有什么不同？不同的运算顺序说明了什么？从而让学生感受到买一样东西付一样钱与两样东西一起买一起付钱结果是一样的.这时，教师再把这个问题抽象成数学问题，学生顺理成章地就明白了相应的道理.有了这样的模型基础，学生在以后的学习中便简单、容易了很多.为了加强学生对知识的理解，我还设计了几个a-b-c式和a-（b+c）式的题目，让学生根据算式编情境，让学生从本质上理解减法的性质，提高学生对知识的理解和掌握程度.所以说如果教师在教授数学概念时能够设置合适的教学情境，将数学概念蕴含在情境中，让学生感受到概念与模型之间的联系，学生的学习自然会轻松很多，教师的课堂教学效果当然也会提高很多.

二、深度挖掘教材内涵，弄清数学概念的本质

根据小学生的年龄特点和接受能力，小学数学教材中的概念以描述式和定义式两种表示方式呈现的最多.所谓定义式就是用简明且完整的语言揭示概念的内涵或外延的方法，例如，“有一个角是直角的三角形是直角三角形”;描述式则是用一些生动、具体的语言对概念进行描述，如，“我们在数物体的时候，用来表示物体个数的1，2，3，4，5，……叫自然数”.

其实，不管是利用哪一种表示方式表示概念，其目的都是一致的，就是便于学生理解、掌握和运用.笔者个人觉得，除了运用不同表示方式表示概念之外，深度挖掘教材内涵，理解概念的本质更为重要，因为只有理解概念的本质才能从根本上对概念进行理解和运用.

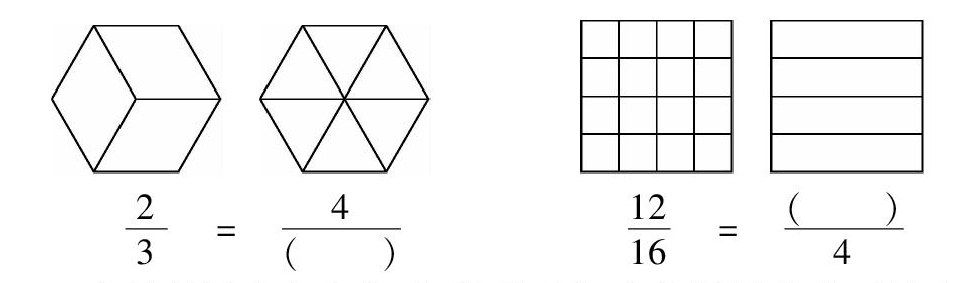
例如，教授“分数的基本性质”一课时，笔者首先设计了一个动手折纸的环节，目的非常明确.一是通过折纸让学生初步感知分数的基本性质——分数的分子和分母同时乘或除以一个相同的数，分数的大小不变;二是通过折纸让学生对分数的基本性质建立初步的模型，即折纸的变化并没有让分数的大小产生变化.之后，笔者设计了第二个教学环节，让学生通过比较、猜测、验证、合作等方式初步得出分数的基本性质，建立对这个概念的表象理解.第三个环节非常重要，笔者设计了三个问题：（1）看到这个性质是不是有一种似曾相识的感觉？（2）和谁相似？（3）哪儿相似？目的是要让学生通过联系旧知识深化对新知识的理解和掌握，同时是要让学生明白知识与知识之间的内在联系，以及分数的基本性质的本质是与“商不变规律”是一样的.在第四个环节笔者设计了一个练习题，让学生看图填一填、涂一涂.

23? =? 4（??? ）

1216? =? （??? ）4

之前教授这个内容时，笔者只把这个题目当成了基本的应用，充其量也就是多了图形的填涂或动手操作而已，只是觉得这个就是体现了新课程标准的一些新思想而已，根本没当回事.是一次市级优课选拔赛改变了笔者对这个题目的看法.因为在一次试教之后反思时，笔者发现这个题目可以用模型思想来解决问题，而且效果更好.从23到46看似将分子、分母同时乘2，实际上不也是把原来每块平均分成2份的过程吗，这里面蕴含着一个“分”的模型思想;从1216到34是将分数的分子和分母同时除以4，实际上不也是将原来每4份合成1份吗，这里面蕴含着一个“合”的模型思想.由此，笔者发现对很多概念，只要深度挖掘，找出概念的本质，运用模型思想解决起来效果会更好.

三、勤于思考，巧用“模型”思想解决疑难问题

记得上班的前几年，每每讲到分数中“分母不能为0”与“分子可以为0”时，总会提到一句话：分数中的分母和分子分别相当于除法中的什么？（除数、被除数）“除数”可以是0吗？（不可以）“被除数”可以是0吗？（可以）所以“分母不能为0，分子可以是0”，并一度觉得这样的解释恰到好处.可是有一次一名学生的一个问题让笔者不得不开始反思自己过往的教学是否真的让学生明白了！学生问道：“老师，为什么除法中‘被除数可以为0而‘除数不能为0呢？”“是啊，为什么呢？”笔者开始思考这个问题.

一次偶然的机会让笔者找到了答案.一个同事家的小孩上三年级刚学除法，遇到了一个问题向笔者请教.幼儿园老师买来60个蛋糕准备分给30个小朋友，问每人可以分几个.给同事家小孩讲解之后笔者对为什么“除数不能为0而被除数可以为0”这个问题也豁然开朗.是啊，除法不就是一个平均分东西的过程吗.被除数不就是物品总数吗，所以当然可以为0，可以理解为没有东西分吗.除数则不同了，除数不就相当于小朋友的人数吗，如果除数是0的话不就相当于一堆东西没人要，那怎么分呢.同样的道理，分数中的问题自然也就迎刃而解了.

由此，笔者不禁在想，如果我们在教学中能够多一些思考，对抽象的问题能多联系旧知识，多运用模型思想帮助学生把新旧知识建立联系，把概念与模型建立联系，我们的数学概念教学定会简单很多，课堂教学的效率自然也会提升不少.

【参考文献】

[1]中华人民共和国教育部.义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社，2012.

[2]范文贵.小学数学教学论[M].上海：华东师范大学出版社，2011.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。