李奋山

摘?要:在力学问题中,有一种动态平衡问题,即由于一个物理量的变化,引起其他物理量缓慢的变化,因为具有一定的综合性,成为高考试题的热点选题。由于其解决方法具有一定的技巧性,所以也是学生学习中的一个难点。解决动态平衡问题的方法主要有解析法、图解法和相似三角形法,不同方法适合不同条件的题目,学生总是分不清楚,下面主要以题目已知条件的多少为线索介绍相应的解题方法。
关键词:动态平衡;力的要素;图解法;相似三角形法
我们常见的问题主要是三个共点力作用下的平衡问题(超过三个力可以通过合成的方法等效为三个力的问题),每个力都有大小、方向、作用点三个要素,三个力应有九个要素,但由于是共点力,所以作用点相同,这样三个力我们只关注大小、方向共六个要素。
一、若六个要素中已知四个(或四个以上)要素,其余两个要素是确定的
如已知两个分力的大小和方向,合力的大小和方向完全是确定的。
如已知合力的大小方向、一个分力的大小方向,根据三角形法则,另一个分力是确定的。
二、若六个要素中已知三个要素,可以用解析法或图解法判断其余三个要素的变化
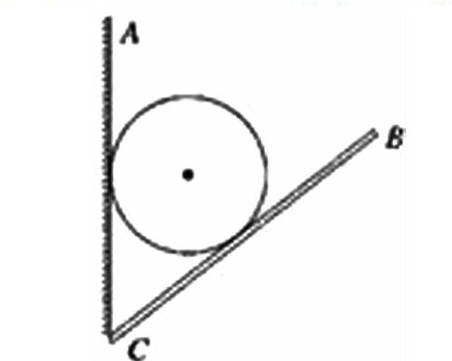
例1.如图所示,把球夹在竖直墙AC和木板BC之间,不计摩擦,墙对球的弹力为N?1?,板对球的弹力为N?2?。在将板BC逐渐放至水平的过程中,关于弹力变化说法正确的是(?)。
A.N?1?和N?2?都增大?B.N?1?和N?2?都减小
C.N?1?增大,N?2?减小?D.N?1?减小,N?2?增大
解析:本题中小球重力的大小和方向,墙对小球的支持力的方向三个要素是确定的,在这种条件下,可以用解析法判断变化情况。
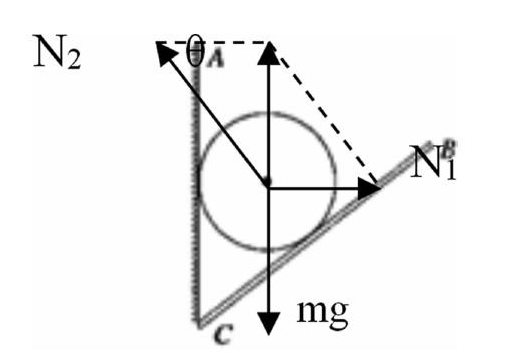
以小球为研究对象,进行受力分析:小球受到重力mg,墙对小球的支持力N?1?和板对球的支持力N?2?。设板与墙间的夹角为θ,在力矢量三角形中,
mgN?1=?tan?θ?得:?N?1=mg?tan?θ
mgN?2=?sin?θ?得:?N?2=mg?sin?θ
将板BC逐渐放至水平的过程中,θ增大,?tan?θ?增大,所以N?1?减小,?sin?θ?增大,N?2?减小。
例2.如图所示,将一光滑小球放在固定斜面和竖直挡板之间,若他将挡板逆时针缓慢转到水平位置,在这一过程中,小球保持静止,斜面和挡板对小球的弹力大小F?1?、F?2?的变化情况正确的是(?)。
A.F?1?逐渐变大?B.F?1?先变小后变大
C.F?2?先变小后变大?D.F?2?逐渐变小
解析:本题中小球重力的大小和方向,斜面对小球的支持力的方向三个要素是确定的,由于板与斜面的夹角变化大于90?0?,正弦、正切的单调性发生变化,解析法不再适合,可用图解法判断。
以小球为研究对象,进行受力分析:小球受到重力mg、斜面对小球的弹力F?1?和挡板对小球的弹力F?2?,三力平衡,任意两个力的合力与第三个力等大反向,作出F?1?,F?2?的合力,这个合力与重力mg等大反向,当挡板绕O点逆时针缓慢地转向水平位置的过程中,F?2?相应的逆时针旋转,做出力的平行四边形,可以看到,F?1?逐渐变小,F?2?先变小,后变大。
三、若六个要素中已知两个要素,可以相似三角形法判断其余四个要素的变化
例3.固定在水平地面上半径为R的光滑半球,球心O的正上方固定一大小可忽略不计的定滑轮,细线一端拴一半径为r的小球,另一端绕过定滑轮.今将小球从下图所示位置A缓慢地拉至顶点B,在小球到达B点前的过程中小球对半球的压力N?/?,细线的拉力F的大小变化情况正确的是(?)。
A.N?/?变大、F变大?B.N?/?变小、F变大
C.N?/?不变、F变小?D.N?/?變大、F变小
解析:本题只有小球重力的大小和方向两个要素是确定的,只能用相似三角形法判断。
以小球为研究对象,进行受力分析,如图所示,小球受到细线的拉力F、半球对小球的支持力N和重力G的作用,由于小球从图中位置被缓慢拉至顶点B,在此过程中小球处于动态平衡状态,小球所受合力为零,拉力F和支持力N的合力与重力等大反向。由图可以看出,几何三角形AOC与由G、N、F构成的三角形相似,有以下比例关系:
NR+r=FL=GR+h
上式中,R、r、h、G均不变,当小球向上运动时,绳长L减小,N不变,F变小,根据牛顿第三定律,小球对半球的压力大小N?/?=N,故N?/?不变。
综上所述:选项C正确。
通过以上分析可以看出,如果有三个要素确定,判断其余三个的变化情形时,可以用解析法或图解法(图解法比解析法的使用范围更广);如果只有两个要素确定,判断其余四个的变化情形时,可以用相似三角形法。通过对已知条件的分析,找出合适的解题方法,以上难点也就迎刃而解了。
- 企业财务成本会计关联面临的问题与对策探讨
- 互联网背景下工商管理模式的创新发展研究
- 互联网时代下生鲜农产品电子商务运营模式创新研究
- 新时期央企基建工程项目党建工作探析
- 企业基层党支部规范化建设的探索
- “五标四创”抓实国企基层党支部党建工作
- 试论国有企业党风廉政建设的强化策略
- 加强农村集体经济管理的有效措施阐述
- 精准扶贫政策下针对信用风险的防范研究
- 船企科研项目动态风险管理研究
- 中小企业人力资源规划存在的问题与对策
- 以创新企业文化提升企业竞争力
- 船舶轮机的维护管理与养护分析
- 数字林场建设中的信息管理系统研制
- 铁路工程项目物资管理现状及优化策略研究
- 论企业核心人才的界定与管理
- 胜任力模型背景下的人力资源管理研究
- 新时期档案管理工作的探析
- 公共管理视角下事业单位行政管理的改革方向
- 信息时代财务会计工作的创新管理
- 杜邦分析法在华茂公司绩效管理中的应用分析
- 严监管背景下农信社合规风险管理体系建设
- 精密装备制造企业科技管理模式的研究
- 浅谈事业单位人力资源管理中的绩效考核
- 基于5G物联网技术的物业管理系统研究
- staffers
- staffing
- staffless
- staff member
- staffs
- staff²
- staff¹
- stag
- stage
- stageabilities
- stageability
- stageable
- stageableness
- stageablenesses
- stageably
- stage-coach
- stagecoach
- stagecoaches
- staged
- stage-diving
- stage-fright
- stage fright
- stage frights
- stageful
- stagefuls
- 醇厚的甜酒
- 醇厚的酒
- 醇古
- 醇味
- 醇和
- 醇善
- 醇嘏
- 醇固
- 醇壹
- 醇备
- 醇学
- 醇德
- 醇懿
- 醇旨
- 醇明
- 醇朗
- 醇朴
- 醇正
- 醇正有价值的文章
- 醇正的香气
- 醇洁
- 醇浓
- 醇淡
- 醇甜
- 醇甿