《运用全息思维优化概念教学》-教育论文，小学教育论文-论文范文参考-科学狗论文网

标题

运用全息思维优化概念教学

范文

【摘要】全息就是全部的信息。全息思维将信息分成显态和潜态两类，人们可以借助全息思维发掘潜态信息的巨大价值。运用全息思维优化数学概念教学，有助于我们走出碎片化的概念教学误区，整体把握概念教学的全过程，建立概念教学的内在秩序，促进学生认知结构的内生长。

【关键词】概念教学;全息思维;知识全息化;方法全息化;过程全息化

【中图分类号】G623.5? 【文献标志码】A? 【文章编号】1005-6009（2019）81-0035-04

【作者简介】李月胜，南京市江宁上坊新城小学（南京，211103）校長，高级教师，南京市数学学科带头人。

全息，顾名思义就是全部的信息。全息思维将信息分成显态和潜态两类，人们可以借助全息思维发掘潜态信息的巨大价值。本文主要阐述如何运用全息思维来优化概念教学。

一、碎片化，当下概念教学的思维样态

（一）缺少整体视野的散点思维

在小学数学概念教学中，有些教师对教材研读的深度不够，只看到本课时的知识要点与预期目标，看不到概念在整个学科系统中、不同学段中乃至知识板块中的结构性关联，甚至就题论题，使得学生对知识与目标的认识呈散点状，缺乏对概念教学的整体设计与结构化把握，这是一种局部的、点状的教学思维。

（二）忽略过程与方法的结果思维

受传统教学影响，一些教师只注重学习结果，简单地将概念的文字形式传递给学生，而忽视概念形成、发展的思维过程，忽略从过程中获得学习方法的路径，这在一定程度上遏制了学生主动探究、自我成长的意识。

（三）忽视互动与生成的静态思维

课堂教学需要充分、周密的课前预设，而预案实施的过程又是互动交流、动态生成的过程。在一些课堂中，师生之间、生生之间缺少多维的信息互动，学生难以碰撞出思维的火花，教师的静态思维使课堂学习失去了师生向上生长的勃勃生机。

二、全息视角，引导概念教学的思维转换

（一）从散点教学转向结构化设计

进行教学设计时，教师应充分了解与所教概念相关的知识结构，着眼于知识结构整体来分析教学内容在知识体系中的地位和作用，确定概念学习的单元目标、学段目标和课程的整体目标，选择与教学内容、教学目标以及学生认知水平相匹配的教学策略，以期实现教学思维结构化。

（二）从关注结果转向过程与结果并重

数学概念的学习不仅要关注概念显态的结果，更应注重获得结果的学习过程及学习方法，即潜态信息转化为显态信息的演绎过程。在教学中，教师应引导学生亲历概念形成和发展的思维过程，从中感悟概念获得的途径和方法，反思成功或失败的探究路径，分析错误产生的原因，提升自主学习的能力。这样，教师的教学思维便能从只关注结果转向学习过程与结果并重。

（三）从习惯静态呈现转向注重动态生成

课堂学习不是按部就班、一成不变的。依据学情，教师的预设是丰富多样的。各种预设都应考虑可能的生成资源，根据课堂的变化形成即时的应对策略，在预设与变化中推进课堂教学，使教学过程从静态呈现转向智慧、精彩的动态生成。

三、整体把握，基于全息思维优化概念教学

在全息思维视角下，信息之间的关系纵横交错，极其丰富。这就要求我们不仅要看到数学概念外显的信息，更要关注概念的潜态信息，并在教学中把数学概念内部的潜态信息尽可能地显现出来，引导学生将潜态信息与显态信息进行重组，体现数学学习的迁移性、逻辑性和整体性。

（一）知识全息化

在全息思维视角下的概念教学中，教师首先应注意知识层面的全息化，引导学生探索、发现概念的表述文字（显态信息）蕴含着哪些与之相关联的隐性的信息要素，实现数学概念在知识层面的全息化。

1.追本溯源，准确把握知识起点。

教材中呈现的概念往往是用简洁扼要的文字来表述的，要弄明白概念是如何产生、形成的，其生长点在哪里，则需要在教学中引导学生追本溯源，使潜态信息显性化。例如：教学苏教版三下《面积的认识》一课，很多教师会从“平面”切入，把面积的学习起点确定为对于“平面”的认识。但一位教师上课时，通过“切土豆”这一活动，让学生感知物体的原有表面（曲面）与剖开的切面（平面）之间的异同，然后再转向研究平面。以“面—平面—平面的大小”的探究路径让学生亲历还原知识的场景，并从中吸收诸多隐性信息：物体表面可凹可凸可平;本节课学习的是其中的平面;等等。

2.延伸拓展，显现知识的隐性内涵。

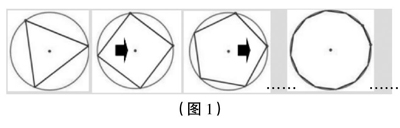
数学概念的潜态信息不仅可以在课始通过追本溯源来显现，还可以在学习过程中对某个节点进行变化拓展，衍生出概念的发展轨迹，体会其中蕴含的数学思想。例如：教学苏教版五下《圆的认识》一课，新课即将结束时，教师安排了一个“赏圆”环节，利用几何画板动态演示“三角形—四边形—五边形—n边形—圆”的过程（如图1），向学生渗透“圆是n边形演变而成的曲线图形”“圆是由无数个点围成的封闭图形”等数学极限思想，把“极限”这一抽象的思想以具象的方式显现出来，让学生感受到奇特的数学美。

（图1）

3.立体沟通，实现知识的空间架构。

如果说追本溯源与变式拓展是某一知识点潜态信息的显性化，概念的知识全息化还必须对相关的知识点进行空间架构，将知识点包含的各种信息要素进行交叉融合，转化成具有内在逻辑结构的、立体的信息结合体，逐步建构知识体系。例如：教学苏教版四上《角的度量》一课，教师从自制的简易量角器切入，根据不断变化的学习需要，引领学生经历成品量角器的发明、创造过程，从而理解量角器是180个单位小角的集合，量角就是测量被测量的角中包含多少个单位小角。这样，就把小学阶段经常使用的直尺与量角器进行了有效的空间架构，即直尺和量角器都是多个测量单位的集合，彰显了数学工具最本质的教育意蕴。

（二）方法全息化

在概念教学中，概念的呈现往往是一种结果式信息，而结果式信息中包含的不仅有知识本身的内在结构和秩序，更有丰富且极具价值的方法信息。这就需要教师高屋建瓴地解读教材，对结果式信息进行全面内化，探寻其形成过程，在发现概念知识结构的同时进一步生成方法和结构。

1.标识串联，形成概念教学的操作路径。

每一个教学环节都包含着众多信息，如教学内容、知识结构、学生认知等。这些信息在教学进程中相互作用，形成外显的、可操作的路径标识，将各种操作标识进行串联，有助于学生逐步形成概念学习的方法结构。例如：蘇教版二下《角的认识》一课的外部信息很多。其中，“角的组成”是从生活原型中抽象出来的，“角的大小”“角的大小与边长的关系”是从做活动角的过程中体验到的。每一环节都是知识与方法相互作用推进的，而推进的学习路径可用如下标识串联起来，即“寻找生活原型—提取数学元素—探究概念内涵—基本练习—回归生活拓展应用”。这样的标识串联可为之后各种平面图形的教学提供可操作的思维路径。

2.策略递进，展现概念教学的层次之美。

数学概念的学习往往不是一蹴而就的。根据知识的内在结构秩序，同一概念常常会被切分成若干层次，分布在不同的年段学习，并在不同年段制定不同的目标序列。将目标序列划分成学段目标后，学段的学习材料、认知目标、学法结构等信息就组成了单元系统新的信息结合体。与内容序列的层次性相匹配，概念学习的策略也应随之递进，构建学习方法的结构层次，展现学法结构的层次之美。

3.组块迁移，内化概念学法的结构秩序。

概念的潜态信息包括知识本身和学习方法等方面的诸多信息元，各个信息元之间相互作用，组合搭配，形成了具有一定规律和秩序的结构，以一定的整体板块形式外显。在教学中，教师应注重调动学生的主动性，激发其内心的体验和感悟，并通过练习运用打通概念之间形式相异、内在相同的同层信息元，将知识结构和方法结构进行恰当移植，引导学生将知识结构转化为自己的认知结构，并在转化过程中获得方法结构。例如：三角形、平行四边形、梯形和圆是小学阶段主要学习的几种平面图形，其中的知识结构是显而易见的，学习方法也具有很强的迁移性。在教学梯形的特征时，就可以移植前面三角形、平行四边形的学习方法。

（三）过程全息化

在概念形成的过程中，其所包含的潜态信息会被逐步地、全向性地发散出去。这就需要教师引导学生亲历概念形成与发展的全过程，在教学中把概念内含的潜态信息尽可能地显现出来，带领学生体会数学的逻辑性和发展性，让概念在学生的思维中慢慢生长。

1.网状互动，促进信息多维流通。

在全息视角下，课堂学习是动态的，互动生成的信息是多维的，涉及知识、方法、时机、情感、生命等方面。课堂上，每个教学环节都内含着互动，有教师与学生之间的互动，也有学生和学生之间的互动，如同桌交流、学习小组内交流、组际交流、全班交流等，课堂交流呈交错的网状结构。这样的信息流动突破了课堂教学的静态思维，改变了教师与少数学生点对点的单一交流，使每个学生都能获得展示的机会。这样，课堂上的各种信息多向度、立体化交叉流动，能有效达成阶段性学习目标，有助于学生认知结构的内生长。

2.适时调控，信息重组创生学习资源。

在开放性问题下，课堂往往会生成许多意想不到的资源，这就要求教师具备一定的教学机智，及时处理好放与收、多元与统整等多重关系，通过不断调整、推进，把这些生成性资源进行结构化、清晰化处理，以实现各种信息的重组，创生出新的学习资源。例如：教学苏教版五上《认识小数》一课，新课开始之前，教师设置了这样一个开放性问题：

师：小数可能是一种什么样的数呢？

生1：小数是比0小的数。

生2（反驳）：小数是比0大，比1小的数。

生3：小数有一位小数、两位小数。

生4：小数中间有个点，这个点把小数分成三个部分。

…………

师：同学们对小数知道得还真不少呢！接下来，我们就来研究小数，看看大家原先对小数的了解是否正确。

上述教学片段中，学生对小数的认识是局部的、分散的，甚至是错误的，教师并没有当即做出评判，而是将这些想法进行分类，并作为本节课探究小数的线索，为后续的学习提供基础性资源。

3.问题回诊，精准把脉学习疑难点。

受认知能力的限制或思维定势的干扰，在学习过程中，预设的学习目标常常不能一次性顺利达成，教师就要针对出现的问题进行“回诊”，从而发现问题的根源所在。学生学习路径中的每一标识都是一个信息结合体，内聚着这一环节潜态和显态的全部信息。教师进行问题回诊时，除了要考查学习策略是否合理，还应检视潜态信息作用下知识目标与学生认知经验、个体差异等构成关系的合理性，具体细致地进行反思，追溯问题根源，精确诊断学生学习过程中的疑点和难点。

总之，运用全息思维优化数学概念教学，探索概念潜态信息显性呈现的有效策略，有助于我们走出碎片化教学误区，全面、立体地关注知识、方法、过程等各个层面的诸多要素，整体把握概念教学的全过程，建立概念教学的内在秩序，促进学生认知结构的内生长。■

【参考文献】

[1]严春友.精神之谜——全息精神学[M].北京：中国社会科学出版社，1991.

[2]夏有恒.全息思维方式论[J].社会科学战线，1995（3）：17-25.

[3]杨世明，王雪琴.数学发现的艺术[M].青岛：青岛海洋大学出版社，1998.

[4]范存丽.让数学思维过程“看得见”[J].人民教育，2014（15）：74-76.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。