《重塑“思考”的含义》-教育论文，小学教育论文-论文范文参考-科学狗论文网

标题

重塑“思考”的含义

范文

丁爱平

【编者按】2019年6月1日—3日，本刊编辑部主办的“求真悟道”2019全国小学数学教育论坛在江苏省南京市第十三中学成功举办。论坛期间，张齐华、朱国荣、罗鸣亮、吴贤、贲友林等名师，围绕本次论坛的主题“关注每一位学生的课堂学习”及其三个维度“倾听”“表达”“思考”执教了研讨课。上一期，我们约请了其中几位作课教师对教学思路展开深度解读。本期《专题研究》栏目，我们呈现几位听课教师对研讨课以及研讨主题的感悟与研究。

摘要：在“求真悟道”2019全国小学数学教育论坛上，贲友林老师执教了《找规律》一课。走进贲老师的这节课，用心探寻“思考”的含义：独立思考——求“真”;多种思考——求“增”;关联思考——求“深”;拓展思考——求“根”。

关键词：找规律独立思考多种思考关联思考拓展思考

2019年6月3日，在“求真悟道”2019全国小学数学教育论坛上，贲友林老师执教了研讨课《找规律》，研讨的主题是“思考”。

贲老师提出，学生的学习应该经历四个阶段：个别想法阶段、多种想法阶段、关联想法阶段、拓展想法阶段。仔细揣摩这四个阶段，我衍生出一些具体的认识：思考，是有方法的，教师如何适时引导？思考，是有品质的，学生应该怎样进阶？思考，是有灵魂的，教师如何发现每一个独特的生命？带着这些原初的认识，我走进贲老师的这节课，用心探寻“思考”的含义。

一、独立思考——求“真”

真正的学习者面对新的问题时，首先不是做一块“海绵”，吸取现成的套装知识，而是留下自己真实的思考。这是个体对新知的第一感，很珍贵。

贲老师精心设计了如下课前学习单，让学生进行充分的独立思考：

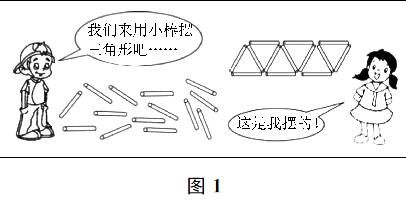
1.如下页图1，像这样摆10个三角形，需要多少根小棒？

我的发现：

我还能提出什么问题？

2.编一道类似的题目。

我编的题目：

我的解答：

师（出示课前学习单的第1题）同桌交流一下，我是怎么想的。

（学生同桌交流。教师巡视。）

师愿意带着材料到前面来，展示给全班看，和全班交流的举手。

（很多学生举手。）

师请谁来呢？我也不认识你们，不知道请谁。（对现场听课教师）请现场不是南京的老师来抽学号。

（一位女教师大声喊：5号！）

师好的，掌声有请5号同学！

（5号学生上台。教师投影展示他的课前学习单。）

师（看材料，报出5号学生姓名：张睿嘉。然后简单地鼓励他大胆讲）我想给张睿嘉一个挑战，到黑板前来讲，这样大家看得见。

（师生来到黑板前。）

师我们先要把这个图画出来，对吧？我来画。（对张睿嘉）你把手臂伸直了，看看有多高。

（张睿嘉伸直手臂。）

师哦，到这儿。好，我就在这里画图。

这个细节打动了我。我们很少想过板书的高度，只记着自己精心预设的结构精巧的板书。而贲老师心里装的始终是学生，黑板是学生的，板书也是学生的。这个细节是“学为中心”课堂理念的自然流露，发乎本心，行于关心。

师我们来画三角形。（画了4个三角形后停下）第10个三角形向上还是向下？

生向上。

生向下。

生向下，因为奇数的向上，偶数的向下。

师梳理一下：3个同学想法不一样，第三个同学是怎么说的？

生他不仅说了向下，而且说了为什么向下。

师我特别欣赏第三个同学的发言，他说出了为什么向下的道理。掌声！

……

个体的思考带有各自的习惯。这里，贲老师引导全班学生聚焦第三个学生的发言，关注表达思考的基本方式，即不仅表达思考的结论，还要说明思考的过程——“是什么”和“为什么”同样重要。这是教师智慧的“导”。

师张睿嘉同学，说说你是怎么想的？给你一个建议：最好圈圈画画，然后再讲。

生（张睿嘉读他的课前学习单）10-1=9（根），9×2=18（根），18+3=21（根）。大家有疑问或补充吗？

（台下立刻小手如林。）

师不急不急！给你一个建议：图在这儿，最好对着图讲。

生（张睿嘉又快速读他的课前学习单）10-1=9（根），9×2=18（根），18+3=21（根）。大家有疑问或补充吗？

（台下又是小手如林。）

师（笑眯眯地）你这次更快了。别急！10表示什么？

生（张睿嘉）10表示向下。

（听课教师顿时骚动起来。贲老师依然笑眯眯地站在张睿嘉身边，安心等待。）

生（张睿嘉）嗯……10表示10个三角形。

师10表示10个三角形，怎么样？

（全班学生报以热烈的掌声。）

生（张睿嘉）10-1=9，9×2……

师慢一点儿。怎么减1？1是什么？

生（张睿嘉）1是1个三角形。

师哪一个三角形？

生（张睿嘉在图中圈出第一个三角形）10-1=9，9×2=18……

师暂停。减掉这个三角形得到9个三角形，对不对？

生（齐）对。

师很好！继续，到9×2。9是9个三角形，没问题。2呢？

生（张睿嘉迟疑一会儿后指图）2是这儿1个三角形，这儿1个三角形。

师那么，9×2——

（张睿嘉迟疑。）

师你可以继續思考，也可以请教别人。

（张睿嘉请第一排的一位男生。）

师换一个人，他刚刚发言过了。

（张睿嘉请后排的一位学生。该生重点解释除去第一个三角形外其他的三角形只用了2根小棒。）

师张睿嘉，你听懂了吗？

（张睿嘉讲得很含糊、混乱。）

师看来刚才同学讲的，你还没有听懂。没关系，继续请教别人。

（在贲老师和其他几位学生的不断引导和帮助下，张睿嘉终于结合图形完整地讲出了算式背后的道理。）

思考的真谛是什么？求真。一个随机报出的5号，引出了一位学习能力比较弱的学生的真实学习情况——在后续研讨中得知，他课前学习单上的算式是家长辅导的。而贲老师不惜耗费近20分钟的时间，等他独立思考、同伴互助、自我调节，帮他找到算式背后的道理。此时，在贲老师的眼里，他是重要的“这一个”。

台下，有听课教师嘀咕：“家常课肯定不能这么上，不能让那么多学生陪练。”其实，贲老师在自己班上也经常随机抽学号请学生展示。如果抽到学力最弱的学生，他会因为没人听课就另换他人吗？当然不会。求真，是个性化思考的行动准则。求真，是“学为中心”课堂的核心要义。不真的思考，从某种意义上说，是课堂的毒药。

二、多种思考——求“增”

师听了张睿嘉的讲解，你看看你和他做的一样吗？

生一样。

生不一样。

师一样的怎么办？不说了。不一样的怎么办？赶紧举手。

生（上台指图）这边有10个三角形，第一个三角形是由3根小棒组成的，其他9个都是由2根小棒组成的。我现在把第一个三角形也看成由2根小棒组成的，那就是2×10=20，再加上刚才去掉的第一个三角形的1根小棒，20+1=21。

（教师引导该生列出综合算式，然后一边在图上圈圈画画，一边讲解。）

生（上台指图）刚才这种方法相当于不看第一根小棒。（同步圈画）我还有一种方法，就是给这张图再补上1根小棒，和原来的第一根小棒再拼成一组“2”，然后把其他小棒2根一组圈起来，这样相当于一共有11个2根小棒，11×2=22;但是补上的这1根小棒并不是真实存在的，所以再把它减去，就是21了。

师这个方法和前面的一样不一样？

生（齐）不一样。

师听了他这个方法，我想到两个字。他先添上1根小棒。假——

生（齐）假设。

师假设再来1根小棒，是吗？这时候就有什么？

生（台上的学生）就有11个2了。我认为前一个同学也运用了假设法：假设这1根小棒不存在。

师太厉害了！既然可以假设增加1根，也可以假设减少1根。听这样的发言太享受了！

……

张睿嘉讲完第一种方法之后，其他学生跃跃欲试，各种方法鱼贯而出。显然，一上来这两种解法来自学生课前深入的思考。因此，贲老师没有过多介入，只是引导讲台上的学生注意讲解的方法，关注座位上的学生有没有投入倾听，并“煽动”他们及时补充、强调。在这个交流多种想法的阶段，每一个学生的认知仓库中都在不断增加着一些东西。

首先是增量。由个别想法增加到多种想法，打开思路。在生生互动中，学生对规律的认识更加具体、全面。正如贲老师经常说的：课堂，不是一枝独秀，要由一个人的思考变成全班的思考，由一个人的精彩变成全班的精彩。

其次是增值。学习多种解法的目的难道仅仅是尽可能多地占有思考的结果吗？当然不止于此！在这个过程中，贲老师侧重让学生关注表达自己思考的方法、触发他人思考的方式，以及对多种解法的审视和概括。这是超越这节课本身所承载的知识和技能目标的，是一种重要的思考力、表達力、合作力的培养，可为学生的未来发展增值。

三、关联思考——求“深”

（还有学生举手。）

师还有第四种方法，是吧？

生（上台）我没有写下来，但是我想到了一种方法。（指图）刚才两个同学都是假设2根小棒为一组，那我可以假设3根小棒为一组。（在黑板上相邻的三角形之间补充一些小棒）这是一个，这也是一个……

师这样，10个三角形都是——

生（台上的学生）独立的。

师（哈哈一笑）本来想让大家说的，结果被你抢到了。独立的三角形，就是说每一个三角形几根小棒？

生（齐）3根。

师（对台下的学生）马上有一个算式。他不说，我们说。

生（齐）3×10-9。

师（对台上的学生）他们说，你赶快写。

（该生板书算式。）

师（对台下一位学生）怎么减9了？

生除了第一个三角形原来就是由3根小棒组成的，后面每一个由2根小棒组成的三角形都加了1根小棒，变成独立的三角形。

师（对台下另一位学生）就加了几根小棒？

（台上的学生指图提示。）

生9根。

师（对台上的学生）你是怎么想到这种方法的？

生我是看了前面两个同学的想法想到的。

师学习就是这样，看到别人的想法就有更多的想法了。

（该生回到座位。其他学生鼓掌。）

师同学们，这道题有人做不出来，怎么帮助他呢？

生可以发明一个公式。我就写了一个：设有n个三角形，（n-1）×2+3。

师有了公式就简单了，可是那公式谁发明呢？他发明不了啊！

生我们还可以列表格，找规律。

师好的，我们来列表格。

（教师在实物展台上铺开一张白纸，画出1个、2个、3个、4个三角形，引导学生观察说出三角形的个数和小棒的根数，同步记录。）

师我如果就这样画下去。你说，我把10个三角形画出来，能不能数出来？

生（齐）能。

师你说，这画、数是不是一种方法？

生（齐）是。

师看着这个表格、这些数据，你有发现吗？

生我发现，小棒的根数依次往上长2根。

师根据他说的，我们把这些数依次读一遍。

生（齐）3、5、7、9。

师小棒的根数依次加——

生2。

生我还发现，小棒的根数总是等于三角形的个数乘2加1。

生也就是上面第二种方法。

……

关联思考就是发现事物之间的联系，从事物之间的关联中寻求事物的发展趋势，从而解决问题、发明创造的思考方法。经历关联思考，学生的思维才能走向深刻、走向批判、走向创新。

小学生进行关联思考，主要分为两类。一是求同关联，同质叠加：运用求同思维，把所有感知到的对象依据一定的标准聚合起来，显示它们的共性和本质。二是求异关联，异质互补：运用求异思维，在联系和发展中，把握认知对象，对具有对立统一特点的地方进行关联。

上述教学片段中，提出第四种方法的学生课前没有想到这种方法，贲老师便追问他是怎么想到的。他说：“我是看了前面两个同学的想法想到的。”贲老师便有意凸显、褒扬：“学习就是这样，看到别人的想法就有更多的想法了！”之后，学生主动关联：“（小棒的根数总是等于三角形的个数乘2加1）也就是上面第二种方法！”着实令人欣喜。

为什么在我们的课堂上，学生不善于关联思考？原因还是在于“教为中心”的陈旧观念。教师精心编排教学环节，象征性地提问：××和××有什么相同？有什么不同？接着请几个“学霸”和自己对话，很快就过去了。长此以往，关联思考的阶段便成为课堂中最冷清的环节，很多学生的关联思维逐渐萎缩。教师应该面向全体学生，提供思考的广阔空间，进行具体的方法指导，并及时回顾、反思，形成习惯，促进学生关联思维的生长，促进深度学习的发生。

四、拓展思考——求“根”

（課尾，教师展示两个没有来上课的学生的课前学习单上的第2题：①摆100个三角形要几根小棒？②用41根小棒可以摆几个三角形？引导学生发现：一个是顺着想的，一个是逆着想的;只要找到规律，都能顺利地解决。）

师很多同学都编了类似摆三角形的问题，老师课前都看了。9号同学的问题很有意思！掌声有请！

（9号学生上台，在黑板上画图，如图2。）

师她的想法不一样在哪儿？

生摞起来了。

师你感觉这里面有没有规律？

生也有一定的规律。

师究竟有什么规律，下课以后研究。（稍停）好了，现在回到第1题。今天上课，你发现，就这个问题，大家的想法怎么样？

生（齐）很多！

师有了不同的想法之后，就要去找它们之间的——

生（齐）联系！

师（指着整个板书，如图3）那你们有没有想过①②③④四种方法之间有什么联系？如果有规律，是什么规律？同学们感兴趣的话，课后继续研究吧！下课！

虽然最后的拓展思考因为时间关系未能充分展开，但是我们鲜明地感受到贲老师独具匠心的教学思想，那就是求“根”：

其一，求知识之“根脉”。这节课研究了“用小棒摆三角形”问题，它的知识根脉是什么？是经历发现规律的过程，初步感悟模型思想。如果看不到这条根脉，课堂很容易变得松散凌乱，变成多种算法的交流会，拘泥于每一个算式，看不到①②③④四种方法背后的过程与思想。

其二，求学习之“根性”。这节课与贲老师其他经典课例一样，有一个共同的特质：学为中心。“学为中心”的课堂以学生的学习活动作为整个教学过程的中心或本体，更多地展现学生学的行为，而非教师教的表现;从学生的学习出发，以学生已有的知识和观念作为新的教学起点，给学生更多的探究和建构的机会，根据学生的学习过程设计相应的促进学生学习的教学活动;不仅仅关注学生学了什么，更关注学生是怎么学的，还关注学生学的态度如何。

其三，求发展之“根本”。课堂是生命成长的地方，要努力让每一个生命都能获得最好的发展。“立德树人”是我们全部思考的终极意义。爱与智慧、大胆独创与合作共赢是学生走向长远发展的必要条件。教师要着力于发挥每一个学生的主体作用，挖掘每一个学生的最大潜力，让每一个学生在自由、民主、合作、愉悦的良好氛围中获得预期的探究发现、意义建构、能力提升，以及身心的全面协调发展。

课已毕，人已散。我久久凝视这一节课的板书（如图3），发现没有一个字是老师写的，连课题都没有。这里，尽情地、自由地舒展着的，是儿童的思考过程，是师生共同走过的学习足迹，是一个大高个和一群小朋友情智相融的美好瞬间……

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。