《高职数学教学中融入数学建模思想的实践》-教育论文，教育论文-论文范文参考-科学狗论文网

网站首页词典首页

标题

高职数学教学中融入数学建模思想的实践

范文

班庆梅甘敏

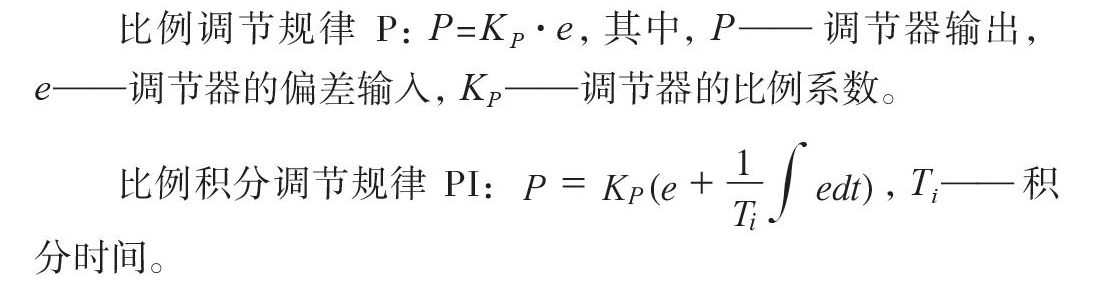
【摘要】本文通过高职数学融入数学建模思想的教学实践，对教学实施的方法及效果进行探究和总结，利用建模思想培养学生应用数学的意识和能力，使学生终身受益。

【关键词】高职数学教学建模思想

【中图分类号】G? 【文献标识码】A

【文章编号】0450-9889（2019）11B-0147-03

高职数学是高职院校培养一线高级技术应用型人才的一门公共基础课和专业工具课，是学生学习专业知识和终身学习的文化基础。为了适应新的要求，必須将以教师为中心，以课堂讲授、知识传授为主的传统高职数学教学模式，转变为以学生为中心，以问题为导向，以培养能力为目标的教学模式，以培养学生应用数学的意识和能力。而这也成为当下高职数学教学的一个探讨课题。

一、教学现状

高职学生数学基础总体薄弱，数学教学课时较少。为了完成教学任务，高职数学课仍采用侧重解题运算、套用公式反复演练、机械模仿或熟记解题技巧等教学方式，学生感到比较枯燥和抽象。为此学生时常提出学习数学有何用处等问题。虽说这种教法对提高学生的抽象思维能力、演绎推理能力有帮助，但对高职学生来说，更应该侧重提高他们的数学应用能力。因此在数学教学中要融入数学建模思想，从简单的初等模型开始，逐步提高。通过“学中做”“做中学”“学用合一”的教学模式，培养学生的数学意识，提高数学应用能力。

二、建模思想

数学建模就是建立数学模型的过程，数学模型简单地说，就是用数学式子（如函数、图形、代数方程、微分方程、积分方程、差分方程等）来描述（表述、模拟）现实事物的存在规律，也就是说，要对实际问题进行分析，发现其中的可以用数学语言来描述的关系或规律，并把这个实际问题化为一个数学问题。求解数学模型，除了要用到数学推理，通常还要处理大量数据，进行大量运算。计算机的出现和迅速发展，给用数学模型解决实际问题打开了广阔道路，也使数学在各行业的应用得到了迅猛的发展。

数学建模是培养学生数学应用能力的良好方法，把它渗透高职数学的日常教学中，无疑给高职数学教学注入新的生机和活力。

三、教学实施

在高职数学教学中，笔者坚持“立足应用，强化能力，融入建模思想，服务专业需求”的原则，重视学生数学应用能力的培养。现以一元函数微积分为例，讲一讲如何以微积分基础知识的掌握为侧重，削弱解题难度的教学措施。

（一）问题教学法

教师根据教学目标和教学知识点，结合教材内容有机地将生活中熟悉的事例抽象成数学问题，以问题情境的方式展开教学。例如，在学习函数这一知识点的时候，将一些关于股票、利润，或者，学校小卖部某物品的月进货量、某同学的月平均体重等事例引入课堂，并针对不同专业的学生进行不同问题的教学设置。例如，航海、轮机专业的航行路程问题、航行经纬度问题，水运管理专业的货物运费问题，等等，使数学教学与学生职业能力的培养紧密相连，突出数学教学职业性，使学生意识到学有所用，进而学以致用。

（二）在教中让学生了解数学知识与专业知识之间的关系

在课堂教学中，教师要将陶行知先生的“教学做合一”理论应用于教学，要不断引导学生探索数学应用问题，培养学生应用意识。教师要让学生从解决一些简单的应用问题开始，也就是说，从学会建立以初等数学为基础的简单数学模型开始，逐步到解决一些较为复杂的问题，比如，线性规划、电力系统、投入产出、运输问题等高等数学范畴的数学问题，有效地提升学生解决实际问题的能力。

同时，教师要多与专业课教师交流，了解相关专业知识，特别要关注专业课程中与数学知识关联之处。例如：

（1）在讲解微分、积分内容时，可以让轮机专业的学生知道，在船舶机舱中，自动化仪器表的应用相当广泛。自动化仪表不仅能在反馈控制系统中对运行参数进行自动控制，而且能对运行参数进行测量和显示。自动化调节器仪表分有比例积分调节器和比例微分调节器，调节器的数据显示是通过微积分知识计算出来的。比如，各种 P、PI、PD、PID 调节器特性，有下面的规律：

比例调节规律 P：P=KP·e，其中，P—— 调节器输出，e—— 调节器的偏差输入，KP—— 调节器的比例系数。

比例积分调节规律 PI：，Ti—— 积分时间。

比例微分调节规律 PD：

，Td—— 微分时间。

比例积分微分调节规律 PID：

。

这些知识的认识对学生学习专业知识有较好的启发作用。

（2）对于机电类专业的学生，可以讲解电流的大小用电流强度描述，其定义式：，是电荷量 q 对时间 t 的导数。对线性电容元件而言，任一瞬时 t，其电压 u、电流 i 的关系也是微分（或积分）的动态关系，即。

（3）对经管类专业，学生要了解弹性问题，知道需求弹性的计算公式：。当价格 p 上涨（或下降）1 个百分点时，需求 Q 下降（或上升）个百分点。例如，某产品的需求函数，需求弹性函数为，EQ∣p=2=-1，即当价格 p=2 时，提价 1 个百分点，需求量减少 1 个百分点。这表明需求量与价格变化的幅度相同，此时价格最优，可获得最大收入。而 EQ∣p=4=-2，当价格 p=4 时，提价 1 个百分点，需求量减少了 2 个百分点。

教师讲授微分知识时，将其融入专业学习中，既有助于提高学生学习兴趣，又能培养学生的数学应用意识。

（三）让学生在学习中结合专业知识加强练习

教学中，教师要注重学生练习，设置问题给学生思考。从简单的专业运算题开始，让学生学习数学建模方法，然后逐步过度到较复杂的专业问题，学会运用微积分知识建立简单的数学模型，并进行求解，循序渐进地培养学生的应用能力。例如：

（1）某轮船由（36°50′N，120°25′W）航行至（25°40′N，140°50′W），求两地间纬差和经差。解答如下：

两地间南纬差11°10′，西经差20°25′。

（2）某轮船真航向 215.5°，测得两物标舷角分别为 QA=030°50′、QB=160°，求 A、B 两物标的真方位。解答如下：

A 物标的真方位 TBA=TC+QA=215.5°+030°50′=246°20′;

B 物標的真方位 TBB=TC+QB=215.5°+160°=375.5°，即? 015°30′。

航海轮机专业的学生在实际工作中，要学会计算船舶的船位。

（3）某航程共同海损的损失总额为 10 万元，共损分摊价值总额为 100 万元，其中，船舶的分摊价值为 60 万元，货物的分摊价值为 35 万元，运费的分摊价值为 5 万元，求各方共同海损的分摊金额。解答如下：

共损分摊率为 10÷100×100%=10%，各方分摊金额为：

船舶共同海损分摊金额：60×10%=6（万元）;

货物共同海损分摊金额：35×10%=3.5（万元）;

运费共同海损分摊金额：5×10%=0.5（万元）。

以上各方分摊的金额之和为 10 万元，即共同海损的损失总额。这类问题要求水运港口管理专业学生能完成。

（4）某公司有 50 套公寓出租，当租金为每月 180 元时会全部租出;当租金每月增加 10 元时，就有一套公寓租不出去;租出去的房子每月需花费 20 元整修维护费。请建立总收入与租金之间的数学模型，当租金定多少可获得最大利润。

对于此题来说，教师要引导学生从模型假设开始，用 R 表示总收入，L 表示利润。设每月租金增加 x 个 10 元，那么其数学模型为 R=（180+10x）（50-x），L=（180+10x-20）（50-x）=（160+10x）（50-x）。让学生用所学微分知识求解，得 L′=340-20x;由 L′=0 可得 x=17，即租金定为 180+10×17=350 元时，获得最大利润。

此类问题的建模求解激发了学生的学习兴趣，使学生在解题过程中的获得感递增，参与度增大。

（5）有三个村庄，由于条件所限，打算合建一所学校，并且共同修筑从小学到各村的道路，小学应该怎么选址，才能使修筑的道路总长度最短。这类建立初等函数模型的问题可留给学生当课后作业，让学生通过学习小组合作完成。

学生在做题中真正体会到数学应用的广泛，懂得数学在工程、生物、经济、环境、能源等各个领域都有广泛的应用。这对学生学会学习、学会合作、学会利用网络和所学知识去解决实际问题有极大的促进作用。

四、实施效果

笔者对不同专业班级的 300 多名学生的实施效果进行问卷调查，结果是，有 90% 的学生认为应该适当做些与专业有关的应用题;有 80% 的学生觉得通过建模思想的融入，提高了对数学课程的兴趣;有 85% 的学生认为按小组互助学习模式来辅助学习数学是可行有效的。

在教学中，融入数学建模思想，使学生通过建模的学习与实践，提高数学知识的应用能力、学习数学的兴趣，并从中找到了为什么要学习数学知识的答案。专业课老师反映，在与数学相关的专业知识教学中，学生变得容易领会了。通过小组互助学习模式，增进了学生团队协作精神。这对学生来说，将会终身受益。

将专业相关知识融入高职数学中，要求教师不断提出与专业课程有关的数学问题，让学生运用数学知识解决问题;要引导学生学会建模，以逐渐提高学生应用数学知识的能力。因此，数学老师除了要提高本专业的知识水平，还要不断了解相关高职专业课程，挖掘更多有专业背景的数学应用问题。为此，对部分有数学特长或对数学建模感兴趣的学生，可以通过开设数学建模选修课、数学建模协会和数学社团等，为这些学生数学应用能力的提高提供平台;也可以选出（下转第164页）（上接第148页）优秀生参加数学建模竞赛，从而多渠道、多方位培养和提高学生的数学应用能力。

【参考文献】

[1]李建军.数学建模 [M].哈尔滨：哈尔滨工业大学出版社，2019

[2]庄小红，向莹，林毅.高职数学教学中融入创新素质培养的实践探索 [J].职教通讯，2017（6）

[3]黄小玉，罗益奎.实施问题教学法培养高职学生的自主学习能力[J].课程教学研究，2015（2）

[4]方金和.轮机自动化[M].大连：大连海事大学出版社，2010

[5]章文俊.航海学[M].大连：大连海事大学出版社，2014

【基金项目】广西教育科学“十三五”规划课题《中高职衔接数学课堂教学有效性的探究与实践》（立项编号：2017C335）。

【作者简介】班庆梅，女，高级讲师，现任教于广西交通运输学校，主要从事中职和高职数学教学与教学研究。

（责编卢建龙）

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。