《变力做功的八种解题方法》-理学论文，物理论文-论文范文参考-科学狗论文网

网站首页词典首页

标题

变力做功的八种解题方法

范文

王理想

摘 ? 要：认真研究总结物理学中的解题思想方法、策略技巧，并能在实际解题过程中灵活应用，可收到事半功倍的效果。本文介绍变力做功的八种解题方法。

关键词：变力;做功;解题;方法

中图分类号：G633.7 文献标识码：A ?文章编号：1003-6148（2015）1-0049-4

1 ? ?微元求和法

把整个过程分成极短的很多段，在极短的每一段里的位移可以看成是直线，力可以看成是恒力，则可用功的公式W=Fxcosθ求每一段元功，再求每小段上做的元功的代数和，即整个过程的总功。

例1 ?解放前后，机械化生产水平较低，人们经常通过“驴拉磨”的方式把粮食颗粒加工成粗面来使用，如图1所示。假设驴拉磨的平均用力大小为500 N，运动的半径为1 m，则驴拉磨转动一周所做的功为多少？

图1 ?驴拉磨

解析 ?将圆周分成很多小段x1，x2，…，xn，拉力在每小段上做的功为W1，W2，…，Wn。因拉力F大小不变，方向始终与物体所在点的速度同向，即力与位移夹角为0°，所以：

W1=Fx1，W2=Fx2，…，Wn=Fxn，

W总=W1+W2+…+Wn=F（x1+x2+…+xn）=F·2πR=1000π J

2 ? ?图像法

F-x图像：在直角坐标系中，用纵坐标表示作用在物体上的力F，横坐标表示物体在力的方向上的位移x，则其F-x图像图线与坐标轴所围成的面积（阴影面积）在数值上等于该段位移内力对物体做的功（如图2）。

图2 ?F-x图像

P-t图像：在直角坐标系中，用纵坐标表示作用在物体上的力F的功率P，横坐标表示力作用在物体上的时间t，则其P-t图像图线与坐标轴所围成的面积（阴影面积）在数值上等于该段位移内力对物体做的功（如图3）。

图3 P-t图像

例2 ?放在粗糙水平面上的物体受到水平拉力的作用，在0～6 s内其速度与时间的图像和该拉力的功率与时间的图像分别如图4甲、乙所示。则0～6 s内物体的位移大小为多少？0～6 s内拉力做的功为多少？

甲 ? ?v-t图像 ? ? ? ? ? ? ? ? ? ? ?乙 ?P-t图像

图4 ?v-t图像和P-t图像

解析 ?由v-t图像面积表示相应时间内的位移，得0～6 s内物体的位移大小为30 m;由P-t图线与坐标轴所围成的面积在数值上等于该段位移内力对物体做的功则W=×2×30+4×10=70 J，所以0～6 s拉力做的功为70 J。

3 ? ?转换变力功为恒力功法

变力做功直接求解时，通常都比较复杂，但若通过转换研究的对象，可以使问题的矛盾转化，有时就可转化变力功为恒力功，可以直接用W=Fxcosθ求解。

例3 ?人在A点拉着绳通过一定滑轮吊起质量m=50 kg的物体，如图5所示。开始绳与水平方向夹角为60°，人匀速提起重物由A点沿水平方向运动2 m到达B点，此时绳与水平方向成30°。求人对绳的拉力做了多少功？（g取10 m/s2）

图5 ?通过定滑轮吊起物体

解析 ?人对绳的拉力做的功与绳对物体的拉力做的功是相同的，又因为人匀速提升物体，故物体处于平衡状态，可知绳上拉力F=mg。所以，人对绳的拉力做功等于重物上升高度Δh中克服重力做的功。Δh由几何关系易求，所以，人对绳子的拉力做的功：

W=mgΔh=1000（-1） J。

4 ? ?转化变力功为平均力功法

在求解变力功时，若物体受力的方向不变，而大小随位移是成线性变化的，即力均匀变化时，则可以认为物体受到一大小为F=的恒力作用，F、F分别为物体初、末态所受到的力，然后用公式P=Fvcosθ求此力所做的功。

例4 ?把长为l的铁钉钉入木板中，每打击一次给予的能量为E0，已知钉子在木板中遇到的阻力与钉子进入木板的深度成正比，比例系数为k。问此钉子全部进入木板需要打击几次？

解析 ?在把钉子打入木板的过程中，钉子把得到的能量用来克服阻力做功，而阻力与钉子进入木板的深度成正比。先求出阻力的平均值，便可得阻力做的功。钉子在整个过程中受到的平均阻力为：

，钉子进入深度l过程中克服阻力做的功为：

，设全过程共打击n次，则给予钉子的总能量：

所以

5 ? ?倍增法

采用如图6所示的装置探究功与物体速度变化的关系。实验中用橡皮筋的弹力拉动小车做功使小车获得动能，探究橡皮筋做的功与小车速度的关系。橡皮筋的弹力是变力，中学教材上没有现成的公式可以计算功的大小。即使知道弹力功的公式也不能用它进行计算，因为橡皮筋的劲度系数也是变化的。但是，在相同的位移情况下，用一条橡皮筋做的功为W，用两条橡皮筋时做的功就是2W，依此类推可以找出功和速度的对应关系。

图6 ?用橡皮筋拉动小车运动

6 ? ?机械能守恒法

机械能守恒定律内容：在只有重力或弹力做功的物体系统内，动能与势能可以相互转化，而总的机械能保持不变。应用机械能守恒定律，无需关注中间过程的细节，只需考虑初、末状态的机械能或动能、势能的变化。因此，机械能守恒定律对解决曲线运动问题应用广泛，经常与圆周运动、平抛运动规律相结合解题。

例5 ?如图7所示，质量m=2 kg的小球系在轻细橡皮条一端，另一端固定在悬点O处。将橡皮条拉直至水平位置OA处（橡皮条无形变）静止释放，小球达O点正下方h=0.5 m处的B点时的速度为v=2 m/s。求小球从A运动到B的过程中橡皮条的弹力对小球所做的功。取g=10 m/s2。

图7 ?小球系于橡皮绳端点

解析橡皮条的弹力是变力，所做的功是变力功无法由公式直接求得。取小球、橡皮条和地球组成的系统为研究对象。在小球从A运动到B的过程中，只有系统内的重力和弹力做功，机械能守恒。取过B点的水平面为零重力势能参考平面，橡皮条为原长时的弹性势能为零，设在B时橡皮条的弹性势能为EP，由机械能守恒定律得mgh=mv2+EP，带入数值得EP=6 J，橡皮条的弹性势能增加6 J，故橡皮条的弹力对小球做功-6 J。

7 ? ?动能定理法

动能定理内容：力在一个过程中对物体所做的功，等于物体在这个过程中动能的变化。动能定理既适用于直线运动，也适用于曲线运动，既适用于求恒力功也适用于求变力功。因使用动能定理可由动能的变化来求功，所以，动能定理是求变力功的首选。

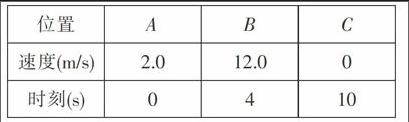
例6 ? 如图8所示，某人乘雪橇从雪坡经A点滑至B点，接着沿水平路面滑至C点停止，人与雪橇的总质量为70 kg。表中记录了沿坡滑下过程中的有关数据，请根据图表中的数据求人与雪橇从A到B的过程中，损失的机械能为多少？

图8 ?人乘雪橇从雪坡下滑

解析 ?物体从A运动到B的过程中，损失的

机械能等于克服摩擦力所做的功。物体从A运动到B的过程中所受的弹力要发生变化，摩擦力大小随之变化，方向也在变。所以，克服摩擦力所做的功不能直接由做功的公式求得。对从A到B过程运用动能定理即可求出物体在AB段克服摩擦力所做的功，即从A到B的过程中损失的机械能。设物体在AB段克服摩擦力所做的功为Wf，由动能定理得： ? ? ? ?，带入数值得Wf=9100 J。所以，人与雪橇从A到B的过程中，损失的机械能为9100 J。

8 ? ?能量守恒法

能量守恒定律内容：能量既不会凭空产生，也不会凭空消失，它只能从一种形式转化为另一种形式，或者从一个物体转移到别的物体，在转化或转移的过程中，能量的总量保持不变。应用能量守恒定律的基本思路：①某种形式的能减少，一定存在其他形式的能增加，且减少量和增加量一定相等;②某个物体的能量减少，一定存在其他物体的能量增加，且减少量和增加量一定相等。

例7 ? 如图9所示，光滑水平面AB与竖直面内的半圆形导轨在B点相切，半圆形导轨的半径为R。一个质量为m的物体将弹簧压缩至A点后由静止释放，在弹力作用下物体获得某一向右的速度后脱离弹簧，当它经过B点进入导轨的瞬间对轨道的压力为其重力的8倍，之后向上运动恰能到达最高点C。（不计空气阻力）试求：

图9 ?物体运行轨道图示

1）物体在A点时弹簧的弹性势能;

2）物体从B点运动至C点的过程中产生的内能。

解析 ?1）设物体在B点的速度为vB，所受弹力为FNB，

则有：

又FNB=8mg，

由能量守恒定律可知：

弹性势能

2）设物体在C点的速度为vC，由题意可知：

物体由B点运动到C点的过程中，由能量守恒定律得：

解得Q=mgR。

（栏目编辑 ?陈 ?洁）

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。