《对功的再认识》-理学论文，物理论文-论文范文参考-科学狗论文网

标题

对功的再认识

范文

张瑶

摘要：功是在认识能量的过程中产生的一个物理概念。历史上对功的认识比对能量的认识晚，其认识过程是一个漫长的历史过程。直到现在，人们还不断地对功进行认识和探究。本文结合物理学史对功进行了再认识，认为不管对功作何理解，都不能脱离“功是能量转化的量度”这一实际意义。

关键词：功；能量；动能；位移；受力质点元

中图分类号：G633.7 文献标识码：A 文章编号：1003-6148（2015）5-0047-3

目前，对功的理解众说纷纭，各自都有一些道理。但有些理解存在欠妥之处，如功的概念，特别是对功的表达式中位移的理解，人们对其争论不休，各执一词。有的认为，该位移是物体的位移，而有的认为该位移应该是作用点的位移，等等。这让很多学习者感到很困惑，特别是对中学生来说，功的概念本来就很抽象，刚接触到功的概念，对功的理解难度就较大，如功的物理意义，计算力做的功时应该用什么位移等。因此，这也引起了不少中学物理教师对这一问题的思考，以及对这一概念的进一步探讨和认识。

本文将从以下三点谈谈笔者对功的认识和理解。

1 历史上对功的认识

科学并没有捷径，道路是曲折而艰辛的。如对功这一概念的认识，并不是像中学生接触这一概念时想象的那么简单，而是经历了很多科学家的努力，最终才使这一概念清晰明了。

对功的认识，可以从笛卡儿学派和莱布尼兹学派关于“运动量度”的一场旷日持久的争论说起。经过对碰撞问题的研究，笛卡尔认为用“运动量”（也就是现在所说的动量）作为物体运动的量度；而莱布尼兹主张用“活力”（也就是现在所说的动能）作为物体运动的度量。莱布尼兹的观点是继承了惠更斯的思想。惠更斯经过碰撞实验的研究后，得到“在两个物体碰撞中，它们的重量及其速度平方乘积之和，在碰撞前后保持不变”的结论，即mv2不变。而导致mv2发生变化的是力对空间的积累效应，这使得功这一概念开始萌芽。

莱布尼茨认为，把重物举到一定的高度。只要重物“大的程度”（也就是现在所说的质量或重力）与被举起的高度的乘积具有相同值，重物将获得相同的“活力”。后来，工程师卡诺在他的论文中，确立了活力与机械功之间的关系，并用重物“大的程度”与被举起的高度的乘积来评价机器的作用，他把这一乘积称为“作用距”。而蒙日把这一乘积称为“动力效应”。之后，科里奥利建议把■mv2作为“活力”，将F·S命名为“功”。并且蓬瑟勒继续保持了这种用法，他采用“千克·米”作为功的单位。现在我们虽继续延用这一概念，但单位是“牛顿·米”，或“焦耳”。

2 对“功是能量转化的量度”这一物理意义的理解

正如本文前面所说，功是力对空间的积累效应，之所以出现这一概念，是为了度量能量变化的多少。从牛顿第二定律F=m■中可以推论出质点动能定理，而功的定义式的依据正是质点动能定理。将上式两边同时点乘元位移dr，即F·dr=m■·dr=m■·dv，在该式中，v是F直接作用的质点的速度，因此如果dr是此受力质点的元位移，那么dr=vdt，则有：

F·dr =mv·dv=d（■mv2）。

即元功d（A）=d（■mv2），此式是质点动能定理的微分形式。

它表明：功是引起动能变化的原因。因此，可以用功来度量动能变化的多少。这只是在机械功的范围，推广到所有非热传递引起的能量的变化，也可以用功来度量。所以说，功的物理意义是“能量转化的量度”，对功的任何理解都不能脱离这一物理意义。

3 对功的表达式中位移的理解

对功的表达式中的位移，引起了很多争论，特别是在中学教学中。由于教学知识的局限性，加上人教版教材《物理2》（必修）对这个位移没有指明是什么的位移，而鲁科版教材《物理2》（必修）把这个位移明确为物体的位移，这就让人更加困惑了。所以，有人说应理解为物体的位移，而有人说应理解为作用点的位移，还有其他一些观点，但持这两种观点的人较多。持第一种观点的人大多都搬出这样一类的例子来证明自己的观点：

例1 人抱在粗糙的电杆上，缓慢往下运动，问人对电杆是否做功？

很显然，根据生活实际，人对电杆是不做功的。理由是，电杆虽然受到人施加的摩擦力，但电杆并没有发生位移，所以人对电杆不做功。如果把表达式中的位移看成作用点的位移，那么人对电杆的摩擦力的作用点是有位移的，所以人对电杆就做了功，这与生活实际相矛盾。

持第二种观点的人大多搬出另外一类例子来证明自己的观点：

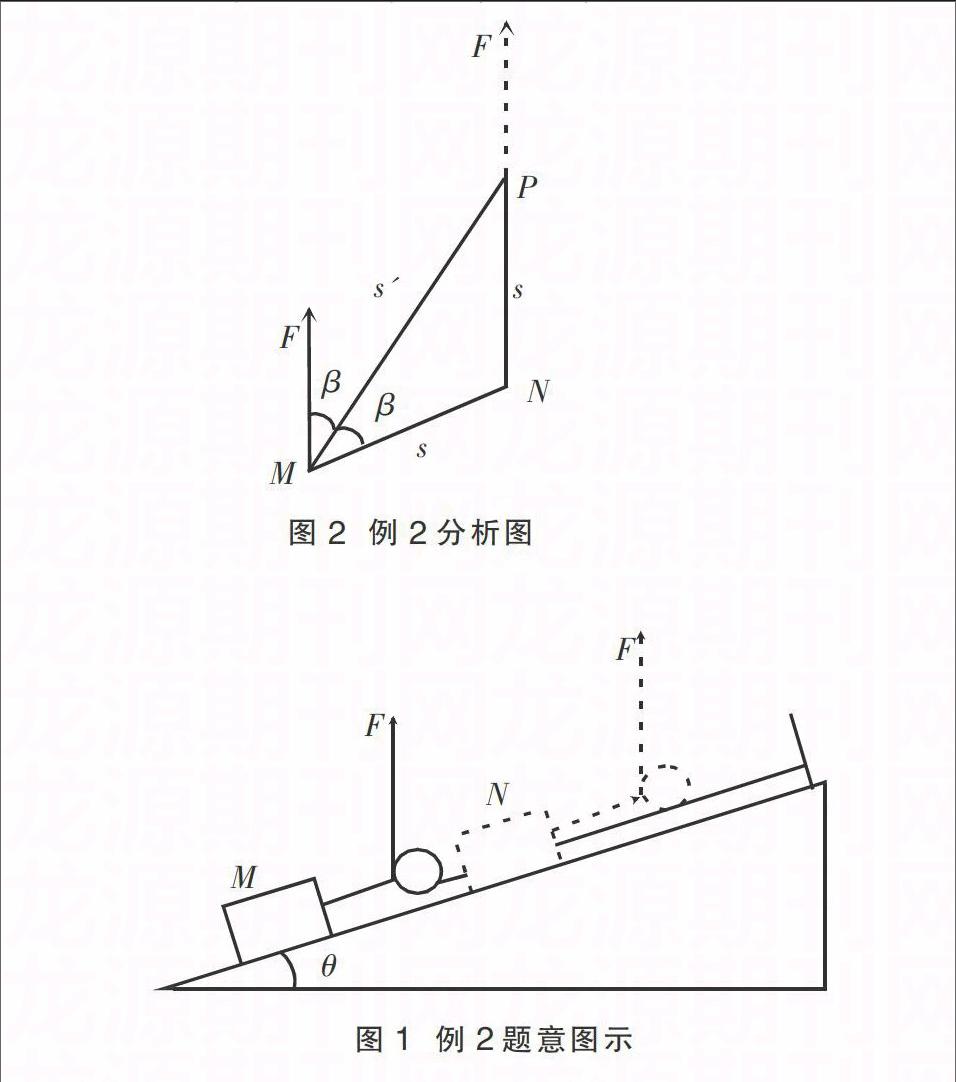
例2 如图1所示，质量为m的物体上固定一光滑滑轮（质量不计），放在倾角为θ的光滑斜面上的M点（用手扶着）。斜面顶端系一根不可伸长的轻绳，轻绳绕过滑轮且与斜面平行，现用一竖直向上的力F拉绳子另一端，使物体缓慢沿斜面向上运动s的距离。问该过程中力F对物体做了多少功？

解析根据功的表达式W=Fscosα，可以证明，题目中的F=■是一个恒力，而位移应该是图2中的s'，而不是物体的s，设F与s'的夹角为β，则s与G'的夹角也为β，且β=■，则：s'=2scosβ。所以，F对物体做的功

W=Fs'cosβ=2Fscos2β=Fs（1+sinθ）。

■

图2 例2分析图

如果将F代入上式，那么，W=mgssinθ，这与实际情况是相符合的。但是，把物体的位移s代入功的计算式，将会得到W=Fssinθ≠mgssinθ，这与实际情况相违背。

其实，无论是哪种理解，都不能脱离“功是能量转化的量度”这一实际意义。从上面质点动能定理的微分式中可以看出，公式中的位移应该是受力质点的位移，不能简单地理解为物体的位移或作用点的位移。这在高等教育出版社出版的普通物理学教程《力学》第四章第2节有明确的表述和论证，功的表达式中位移是受力质点元的位移。

如果受力物体是刚体，且刚体只有平动，例1中的观点是正确的。这种情况下，只是受力质点元发生了转移，并非位移。如果只局限于中学物理知识范围，可以认为受力质点元和力的作用点重合，例2的观点也是正确的。

但是，位移是一个相对量，在计算功时，要明确受力质点元的位移是相对于哪个参考系的位移。从下面的例子可以看出。

例3 在倾角为θ的粗糙斜面上有一半径为R的圆柱体，由静止开始无相对滑动地滚下。求斜面对圆柱体做的功？

解析首先，要明确该题中的摩擦力为滚动摩擦力。若选斜面为参考系，则摩擦力不做功，圆柱体的机械能守恒。因为对于斜面，圆柱体受力质点元没有发生位移，故摩擦力做功为零；若选圆柱体的中心轴为参考系，那么摩擦力做功，使圆柱体的部分平动能转化成了转动能，但是转化的过程中并不消耗机械能。

总之，对功的理解，应该结合物理学史，不能背离功的实际意义，那么对功就不难理解。跳出中学物理知识的局限范围，可以发现，功的表达式中的位移指的是受力质点元的位移，并不能简单地认为是物体的位移或作用点的位移。

参考文献：

[1]弗·卡约里，等.物理学史[M].北京：中国人民大学出版社，1962.

[2]申先甲，等.物理学史[M].长沙：湖南人民出版社，1994.

[3]朱荣华.物理学基本概念的历史发展[M].北京：冶金工业出版社，1987.

[4]漆安慎，杜婵英.力学[M].北京：高等教育出版社，1997.

[5]黄正玉.功的计算到底是用物体位移还是作用点位移[J].物理通报，2013，（10）：103.

[6]费宏.关于功概念的争论与有关疑难问题的研究[J].物理教师，2012，33（10）：24.

[7]赵坚.如何正确理解功的定义式中的位移“s”[J].物理教师，2010，31（1）：40.

[8]胡欢欢.浅谈做功公式中的位移[J].物理通报，2013，（z2）：113.

（栏目编辑陈洁）

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。