网站首页  词典首页

请输入您要查询的论文：

　

标题 CFD软件及源程序辅助工程流体力学课程教学的探索与实践
范文 蒋光彪　殷水平　陈胜铭




摘要：工程流体力学课程具有较强的理论性，涉及的知识面也较宽广，给该门课程的教与学带来较大的影响。文章针对工程流体力学课程的这些特点，结合多年来的教学实践，将CFD软件和源程序的强大数值模拟功能，引入工程流体力学课程辅助教学中，通过利用CFD软件和源程序进行数值模拟教学这一环节，探讨流体力学课程对接科研成果的教学模式。实践证明，这一模式获得了较好的教学效果。
关键词：工程流体力学；计算流体力学；CFD软件及源程序；教学研究
中图分类号：G6420；TU 文献标志码：A 文章编号：10052909（2015）05015404
一、工程流体力学与CFD软件、源程序
计算流体力学（Computational Fluid Dynamics，简称CFD）软件通过计算机数值计算和图像显示后处理，对包含流体流动和有热传导等相关物理现象作出系统的分析。目前，CFD 技术已经广泛应用到航空、航天、气象、船舶、水利、化工、建筑、机械、汽车、海洋、体育、环境等领域，取得了令人瞩目的成就。在现代科学技术高度发展的今天，计算技术已被引入到流体力学领域，使以前因计算过于复杂而影响进一步探讨的流体力学问题逐步得以解决，计算流体力学已经成为研究流体力学的重要方法[1-3]。常用的CFD计算软件有FLUENT 、CFX、Phoenix等。FLUENT 软件是目前常用的一套高性能的数值软件，是专门针对流体工程数值计算与仿真需求而开发的一种流体数值仿真软件。
工程流体力学课程教学内容主要分为流体静力学、流体动力学、相似和量纲分析、管中流动、孔口出流和缝隙流动等[4]。其中，管中流动主要研究圆管中的层流及紊流、管路中的沿程阻力、管路中的局部阻力及管路计算等，涉及到一系列的概念和理论公式，学生理解起来有点枯燥、困难[4-5]。通过利用FLUENT软件和源程序进行数值模拟这一环节，变枯燥的理论公式计算为生动的计算机数值求解，既提高了学生的学习兴趣，同时也使学生有了更多的感性认识和理性认识，增强学生解决实际问题的能力。在流体力学课程教学中， 有意识地穿插计算数学、Fortran语言编程、CFD知识，有助于学生理解流体力学公式及方程，
也可以加强学生对其他学科知识的理解和掌握，达到多学科之间的融会贯通， 触类旁通。为此，笔者对科研成果中相关源源程序、部分开源程序和CFD 软件在工程流体力学课程教学中的应用做了一些探索与实践。
二、 教学案例
（一） 圆管中的层流及紊流教学实例
在工程流体力学教学中，管中流动是主要章节的内容，涉及的理论和公式多，不易理解。圆管流动有层流和紊流两种流动状况。雷诺数是判别流体流动状态的准则数。为加深学生对流速分布和压强分布规律的理解，在教学中可安排课外作业，设置用FLUENT软件来模拟研究三维圆管的层流和紊流流动状况，作出验证分析。
图1为圆管流动入口和出口边界截面的流速分布图（l=2m， d=0.1m）。取流动充分发展部分，离入流边界x/D=1.6的截面其流速分布如图2所示。可以看出流速沿半径Y方向成抛物线分布，与书中理论公式相符，如式（1）所示。通过数值模拟，学生对圆管内流动速度分布有了更深刻的认识。
由图3可以看出圆管内部压强分布从管口处向延伸方向逐渐减小，可知流速相应增大，符合流速大、压强小的流动定律，也符合圆管流动压降的原理。另外从入口处的压强分布可以看出，在圆管任何截面上，其压强分布也不是均匀的，也有分层现象。＼
图 3 圆管内部压强分布
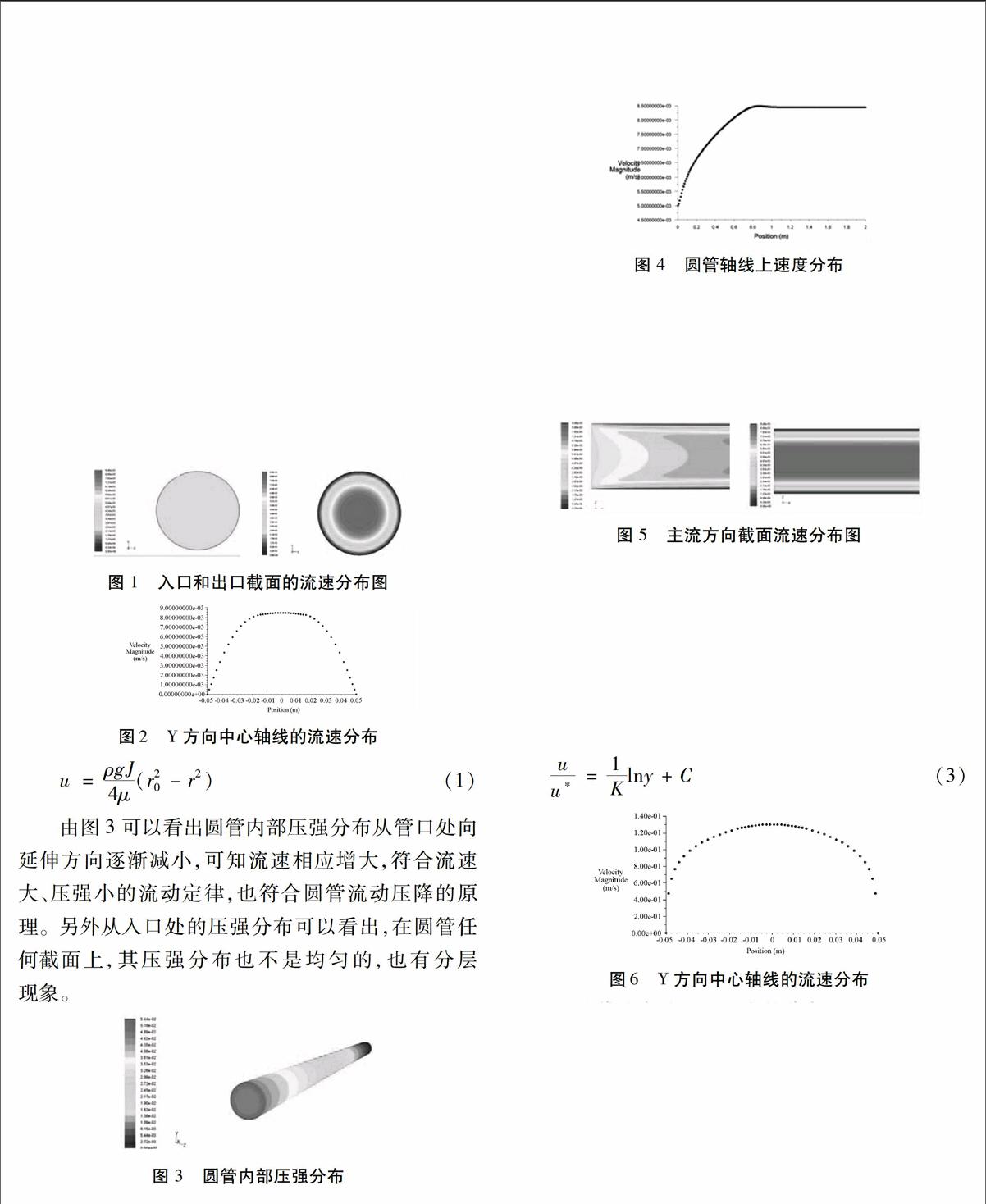
图4为圆管轴线上的速度分布。由图可以看出，在圆管的轴上，进口段流速分布变化较大，从进口流速v1=0.005m/s急剧上升到最大流速umax=0.00 848m/s。层流入口段长度有经验公式可以算的，即
L≈0.058 dRe （2）
可算得入口段长度约为1.18m，由图4显示效果可以看出，流速在离入口1.1m到1.2m之间，即入口段长度约为1.1～1.2m，符合书中理论计算结果。
图 4 圆管轴线上速度分布
图5为圆管内部x轴方向不同截面的流速分布，可看出流速在截面上从入口到出口的变化。水流在圆管内部的流速分层很明显，靠近壁面处流速接近于零。
图 5 主流方向截面流速分布图
图6为圆管紊流充分发展段某一截面的流速分布图。从图中可以看出在紊流充分发展段，截面流速散点图最高处几乎为一条直线，说明圆管内大多数流体流速趋于稳定，而是更加平滑。紊流过流断面的流速对数分布比层流的抛物面分布均匀得多，这在理论上符合紊流流速的对数分布律，即：
uu=1Klny+C（3）
图6 Y方向中心轴线的流速分布
（二）管路中的沿程阻力教学实例
在流体力学教学内容管中流动一章的教学实践中，笔者利用前期研发的程序[6]设置了以半扩散角为4o、扩散度为3.92的锥形渐扩管路内的不可压缩流动数值模拟算例，旨在将对接科研成果的教学模式用于辅助工程流体力学课程教学实践。已知条件：锥形渐扩管路前接管直径为30 mm，后续管直径为50 mm，总长度为70 mm。管内流动介质为空气，进口速度为1m/s。 网格模型如图7所示。
图7 锥形渐扩管路系统内流场网格模型
数值计算结果如图8所示。从图中可清晰看出，在突然扩大段，压力逐渐增大，表现扩压效果，但中心线上的速度呈下降趋，若扩散角增大时，在渐扩段会出现局部回流区，这是造成局部能量损失的重要原因。
图8 锥形渐扩管路内压力场
局部阻力误差分析：对于锥形渐扩管的局部阻力，可以用包达定理的形式表示：
hζ=ku1-u222g（4）
其中，k为经验系数。由式可知，锥形渐扩管局部阻力损失理论计算公式为：
hz = ku1 - u2 22g = k1 - A1 A2 2×u21 2g = k1 - A2 A1 2×u22 2g（5）
其中A1为渐扩管上游横截面积，A2为渐扩管下游横截面积（m2），u1为渐扩管上游平均流速（理论值），u2为渐扩管下游平均流速（理论值）。A1 = πd21 4 = π×124，A2 = πd22 4 = π×224，u1=1 m/s，g=9.8m/s2 。代入（5）式得：
hζ理=0.004 305 m
实际流体的伯努利方程为[7]：
Z1 + P1 ρg + u21 2g = Z2 + P2 ρg + u22 2g + hf + hζ （6）
将仿真结果代入上式，其中Z1=Z2=0 P1=-0.03pa，P2=0.4pa，u1=1.06m/s， u2=0.58 m/s， hf=0， 得 hζ模拟=0.00 435m。误差率为：
η=hζ模-hζ理hζ模×100%
=0.00 435-0.004 3050.00 435×100%=1.03%
（三） 后台阶流动教学实例
为让学生对雷诺数有更进一步的感性认识，利用开源CFD程序[8]可设置后台阶流动教学实例，比较不同入流Re数时台阶后涡的大小和长度，现选择四种Re数工况的计算结果进行后处理，得到如图9所示的流线图。从图中可以看出，随Re数的增加，台阶后方主涡的大小呈增大趋势，在Re=1 000时在上方有次生涡的出现。
图9 不同雷诺数下的流线图
三、 教学实践中的几点体会
（一） 理论教学与数值实验教学的合理利用
在工程流体力学理论教学时可结合数值实验教学加以辅助，例如在管中流动一章教学时，可以用上述相关教学实例。由于在进行课堂演示教学时，依计算机性能及不同问题的规模难易程度，数值模拟求解的时间将有不同，要掌握合理数值模拟时间。可采取让学生安装CFD程序及软件，并要求学生事先自学使用方法，尝试数值预测，预习理论知识。然后教师理论教学时对学生预测结果进行抽样调查分析，将理论结果与计算结果比较分析。条件许可的话，也可以通过高性能集群提交计算作业，在较短的时间内获得计算结果。这样学生对复杂的理论就能有深入的认识，同时也锻炼了学生的科研能力。
（二）适当安排精选案例教学
课堂教学演示案例的选取应做到简单且具有代表性。 案例简单能够减少计算机的运行时间，使教学更加紧凑；而有代表性的案例贴近生活或工程实际，则有利于提高教学趣味，开阔学生的视野。由于课堂教学时间有限，因此应在简单演示教学案例的基础上，精心布置较为复杂的课外任务。
（三） 源程序和软件互补
在数值模拟教学中结合利用软件和程序。软件不是万能的，商用软件所能解决的问题是已在学术界得到充分研究的问题，对于科学研究来说，自己编程是必不可少的。一方面，自编程能更好地理解CFD具体实施过程，对商用软件的理解和使用也是有帮助的。另一方面，自编程序还可以更好地对接科研成果，用于工程流体力学课程辅助教学。
四、结 语
通过上述几个数值模拟实例可以看出，数值模拟过程并不太难，但结果更形象直观。借助计算机辅助手段，在工程流体力学课堂教学中，利用CFD软件及源程序进行数值模拟辅助理论教学， 将理论性较强的内容形象化，可以开阔学生的视野， 激发学生的学习兴趣和创新意识， 加深学生对基础理论的理解。此外，通过对接科研成果，用源程序进行数值实验教学还可以培养学生的动手能力和科研能力，丰富数值实验教学内容。参考文献：
[1]J.H. Ferziger， M.Peric.， Computational Method for Fluid Dynamics[M]. Springer，2002.
[2]张涵信，沈孟育.计算流体力学—差分方法的原理和应用 [M]. 北京： 国防工业出版社，2003.
[3]傅德薰，马延文.计算流体力学[M]. 北京： 高等教育出版社，2000.
[4]张也影.流体力学[M].2版.高等教育出版社，2009.
[5]郑捷庆，邹锋，张军，等. CFD软件在工程流体力学教学中的应用[J]. 中国现代教育装备， 2007（10）：119-121.
[6]何永森，舒适，蒋光彪，等.管路内流体数值计算与仿真[M]. 湖南 湘潭： 湘潭大学出版社，2011.
[7]章梓雄，董曾南.粘性流体力学[M]. 北京： 清华大学出版社，1998.
[8]URL： ftp：//ftp.springer. de/pub/technik/peric/（web Page）.
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2024/12/23 8:35:44