《基于符号检测辅助的MMSE与LS干扰对齐算法研究》-工学论文，软件工程论文-论文范文参考-科学狗论文网

标题

基于符号检测辅助的MMSE与LS干扰对齐算法研究

范文

贾国庆张寒

摘要：干扰对齐（IA）是一种有效消除干扰的管理机制。为了彻底消除干扰信号对期望信号的影响，通过预编码技术处理使干扰在接收端重叠，使接收端的干扰信号与期望信号有效分开。在传统最小均方误差（Minimum Mean Square Error，MMSE）算法和最小二乘（least square，LS）算法基础上，提出基于符号检测辅助的最小均方误差（Symbol Detection Aided Minimum Mean Square Error，SDA-MMSE）算法和最小二乘（Symbol Detection Aided Least Square，SDA-LS）算法。分别基于传统算法和改进算法进行迭代计算，通过仿真可看出SDA-MMSE算法的MSE较SDA-LS算法的MSE降低约20%。理论分析与仿真结果表明，改进算法较传统算法具有更好的系统性能，且SDA-MMSE算法系统性能最优。

关键词：干扰对齐;符号检测;最小均方误差;最小二乘算法

DOI：10. 11907/rjdk. 191305 开放科学（资源服务）标识码（OSID）：

中图分类号：TP312文献标识码：A 文章编号：1672-7800（2019）009-0072-05

MMSE and LS Interference Alignment Algorithm Based on Symbol Detection

JIA Guo-qing，ZHANG Han

（School of Physics & Electronic Information Engineering，Qinghai Nationalities University，Xining 810007，China）

Abstract：Interference alignment （IA） is an effective management mechanism for eliminating interference. In order to eliminate the influence of interference signal on the desired signal thoroughly， we use precoding technology to process the interference at the receiver so that the interference signal at the receiver can be effectively separated from the desired signal. In this paper， a symbol detection aided minimum mean square error （SDA - MMSE） algorithm and a symbol detection aided least squares （SDA - LS） algorithm based on symbol detection are proposed on the traditional MMSE algorithm and LS algorithm. Firstly， the iterative calculation is carried out based on the traditional algorithm， and then the iterative calculation is carried out by using the improved algorithm. The simulation results show that the MSE of SDA-MMSE algorithm is about 20% lower than that of SDA-LS algorithm. The theoretical analysis and results show that the proposed algorithm has better system performance than the traditional algorithm， and the performance of SDA-MMSE algorithm is the best.

Key Words： interference alignment;symbol detection;minimum mean square error;least square algorithm

0 引言

多入多出（Multiple-Input Multiple-Output，MIMO）是第四代移動通信关键技术之一，不断增加系统带宽和天线发射功率可以显著提高信道容量及频谱利用率[1]。对单一用户 MIMO系统，若配置的天线数受限会使系统降低所获得的容量增益，而多用户 MIMO 系统允许多个用户同时进行通信传输，可达到更高的容量。但天线数目和用户数量增加时会引起无线介质的广播与叠加，此时产生的干扰成为制约多用户 MIMO 系统可靠通信的重要因素之一[2]。因此，为了改善系统性能，需采用有效措施对用户引起的干扰进行管理。

随着无线通信网络的发展，信道中的干扰成为限制无线通信网络系统性能的瓶颈，近年来也有一些干扰管理方法被提出，比如干扰信号解调消除方法[3-5]、对干扰以噪声形式剔除的方法[6-8]以及干扰对齐（Interference Alignment，IA）技术[9]。

在各种网络拓扑中，干扰对齐技术得到广泛应用，如干扰信道[10-14]、干扰多址接入信道[15]、干扰广播信道[16]、具有中继的信道[17]等。干扰对齐可以使干扰信号在接收端重叠，降低干扰信号所占用的资源，减弱干扰信号对有用信号的影响，能更好地管理干扰[18-19]。当前，随着用户数的不断增加，干扰问题也变得愈加严重，发射端预编码的设计显得更为重要。通过适当的预编码，可以有效控制多用户之间的干扰，从而大大提高多用户系统容量[20]。

干扰对齐作为一种干扰消除技术，能在高信噪比情况下获得很好的系统容量。另外，在优化不同标准的基础上，大量的迭代收发器设计方法被提出和研究[21-22]。传统算法没有考虑数据流的影响，特别是在数据流非常小的情况下是不合理的。鉴于此，本文提出传统算法基础上符号检测辅助的干扰对齐算法，它是两种基于传统算法迭代收发器联合设计的算法。一种是辅助最小均方（MMSE）误差干扰对齐的符号检测技术，它是一种基于最小均方误差的迭代收发器联合设计的符号检测算法;另一种是辅助最小二乘（LS）的符号检测技术，它是一种基于最小二乘的迭代收发器联合设计的符号检测算法[23-25]。通过系统仿真验证了这两者改进干扰对齐方法均比传统干扰对齐算法具有更好的系统性能;并且通过比较发现SDA-MMSE算法比SDA-LS算法有更好的系统性能，可以更好地抑制干扰。

1 系统模型

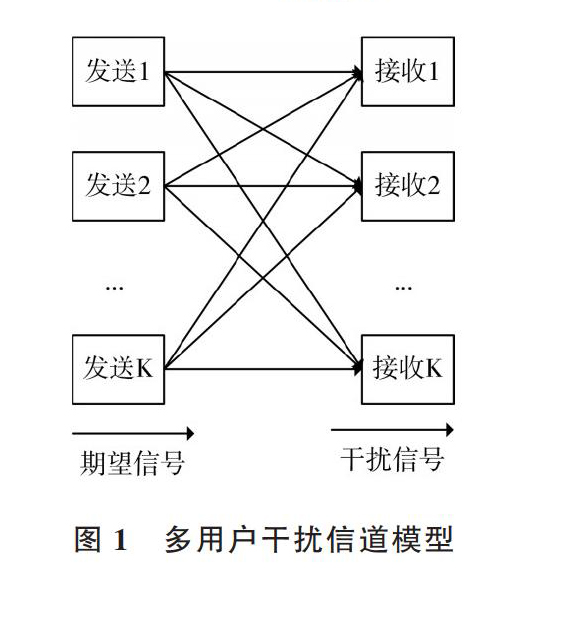
如图1所示的[K]用户MIMO-OFDM干扰信道，[K]个发射机分别独立地同时发送数据给[K]个接收机，接收机既能接收到期望信号，也能接收到来自于其它发射机的干扰。在无线干扰信道中，每个发射机仅尝试与一个接收机通信。进一步讲，每个发射机上带有的[N]个天线发送[d]个独立的数据流与相应接收器上的[M]个天线进行通信。则第[i]个接收机接收的数据可以表示为：

2 算法描述

2.1 MMSE算法

根据MMSE标准，[Ui]的求解可根据以下推导出：

为了满足式（3-4）的IA条件，首先将矩阵[Vi]初始化，使矩阵[Vi]为一个随机的单式矩阵，然后将式（10）和式（11）进行迭代计算直到迭代结束或达到某些条件满足[K]个用户，得到的数据流即为所需。

2.1.2 改进MMSE算法

实际上，传统算法根据式（7）、式（8）期望得到的式（10）、式（11）并不严格等于后者，尤其是当总传输数据流数较小时。本文给出一种基于式（7）、式（8）使[sj=sj]的改进算法。

2.2 LS算法

LS算法与MMSE算法类似，在算法设计中仅仅是将噪声看作零。

2.2.1 传统LS算法

傳统LS算法认为在迭代计算中收发器不与码流相关，为剔除干扰符号流[sj];传统LS算法把对[Ui]和[Vi]的期望转变为对数据流[sj]的期望。通常情况下，符号流[sj]满足以下条件：

为了满足式（3）、式（4）的IA条件，首先将矩阵[Vi]初始化为一个随机的单式矩阵，然后将式（15）和式（16）进行迭代计算直到迭代结束或者达到某些条件满足[K]个用户，最后根据[Ui]和[Vi]检测得到的数据流即为所需。

2.2.2 改进LS算法

首先，利用LS传统算法进行迭代计算出预编码矩阵[Ui]和[Vi]，然后通过符号检测，最后根据[sj=sj]再一次迭代计算[Ui]和[Vi]，因此得到最优[Ui]和[Vi]如下：

3 性能分析与仿真

仿真结果是在[K=3]，[N=4]，[M=4]，[d=2]条件下得到，首先基于传统算法设计收发机的预编码矩阵[Ui]和抑制矩阵[Vi]，进行符号检测得到[si]，然后将检测符号[si]代入本文改进算法中，再进行[Ui]和[Vi]的迭代计算，直至干扰已对齐。每个节点用QPSK的调制方式，分别对MMSE、SDA-MMSE和LS、SDA-LS进行仿真，分别作出这4种符号检测算法的均方误差（Mean Squared Error，MSE）与迭代次数的关系曲线、误码率（Beat Error Rate，BER）与信噪比（Signal Noise Ratio，SNR）的关系曲线，如图2-图5所示。

图2和图3中的仿真参数：信噪比SNR=15dB，[α]=7，[β]=93，信道遍历次数为100 000。对比图2和图3可以看出， SDA-LS干扰对齐算法与SDA-MMSE干扰对齐算法在同一迭代次数下，SDA-MMSE算法检测得到的符号更加接近发送符号，且SDA-MMSE算法的MSE相比SDA-LS算法的MSE降低约20%，因此SDA-MMSE算法有更好的系统性能。

图4和图5是两种算法下SNR与BER的关系曲线。SNR取0～15dB，通过增加信噪比，本文提出的两种改进干扰对齐算法均可获得比传统干扰对齐算法更好的BER性能，尤其是在高SNR区域。并且SDA-MMSE 算法的误码率较 SDA-LS 算法低，例如在15dB时，SDA-MMSE算法比SDA-LS 算法约有8个dB的增益，因此SDA-MMSE算法的BER性能更优。

4 结语

为了更好地消除多用户间的干扰，本文在传统算法基础上针对在数据流较小的缺点，提出了两种基于符号检测的干扰对齐算法：SDA-MMSE算法和SDA-LS算法。从均方误差与误码率方面证明改进算法均优于传统算法，本文提出的算法因为符号检测的增益较传统干扰对齐算法具有更好的MSE和BER性能，并且得到SDA-MMSE 算法的性能最优。但在算法迭代计算过程中没有考虑到复杂度的变化，后续研究可考虑在改进算法基础上降低复杂度。

参考文献：

[1] EMRE T. Capacity of ?multi-antenna ?gaussian ?channels[J]. ?European ?Transactions on Telecommunications，1999，10（6）：585-595.

[2] ZHANG S L，LIEW C S，CHEN J Y. The capacity of known interference channel[J]. IEEE Journal on Selected Areas in Communications，2015，33（6）：1241-1252.

[3] CARLEIAI A B. A Case where interference does not reduce capacity[J]. IEEE Transactions on information Theory，1975，21（5）：569-570.

[4] T HAN， KPBAYASHI K. A new achievable rate region for the interference channel[J]. IEEE Transaction on Information Theory，1981，27（1）：49-60.

[5] SATO H. The capacity of the Gaussian interference channel under strong interference[J]. IEEE Transaction on Information Theory，1981，27：786-788.

[6] ETKIN R H，TSE D N C， H WANG. Gaussian interference channel capacity to within one bit[J]. IEEE Transaction on Information Theory，2008，54（12）：5534-5562.

[7] MOTAHARI A S，KHANDANI A K. Capacity bounds for Gaussian interference channel[J]. IEEE Transaction on Information Theory，2009，55（2）：620-643.

[8] SHANG X，KRAMER G，CHEN B. A new outer bound and the noisy interference sumrate capacity for Gaussian interference channels[J]. IEEE Transaction on Information Theory，2009，55（2）：689-699.

[9] FALAHATI A，AKVARI M. Interference alignment in space time and frequency achievable DOF analysis[J]. Electronics Lett.，2016，52（3）：204-206.

[10] XIE J W，ULUKUS S. Secure degrees of freedom of K-user Gaussian interference channels： a unified view[J]. IEEE ?Transactions ?on ?Information ?Theory，2015，61（5）：2647-2660.

[11] ZONG Z ?Y，FENG H，YU F R，et al. Optimal transceiver design for SWIPT in K-user MIMO interference channels[J]. IEEE Transactions on Wireless Communications，2016，15（1）：430-455.

[12] JOHNNY M，AREF M R. An efficient precoder size for interference alignment of the K-user interference channel[J]. IEEE Communications Letters，2017，21（9）：1941-1944.

[13] PANAHI F H，OHTSUKI T，JIANG W J，et al. Joint interference alignment and power alloction for multi-user MIMO interference channels under perfect and imperfect CSI[J]. IEEE Communications Letters，2017，1（2）：131-144.

[14] ZHAO N，YU F R，JIN M L，et ?al. Interference ?alignment and ?its ?applications： a ?survey，research ?issues，and ?challenges[J]. IEEE Communications Survey &Tutorials，2016，18（3）：1779-1803.

[15] SHIN W，LEE J. Retrospective ?interference ?alignment ?for the two cell MIMO interfering multiple access channel[J]. IEEE ?Transactions ?on ?Wireless ?Communications，2015，14（7）：3937-3947.

[16] TANG J，SO D K ?C，ALSUSA E，et ?al. Energy ?efficiency optimization with interference alignment in multicell MIMO interfering broadcast channels[J]. IEEE Transactions on Communications，2015，63（7）：2486-2499.

[17] LI X，SUN Y，ZHAO N，et al. A ?novel ?interference ?alignment ?scheme with ?a ?full-duplex MIMO ?relay[J]. IEEE Communications Letter，2015，19（10）： 1798-1801.

[18] 王勤民，張忠培，结凤克，等. 干扰对齐的分集检测算法研究[J]. 电子与信息学报，2012，34（6）：1393-1397.

[19] 凌必祥，解培中，李汀. Stiefel流形上的单边干扰对齐预编码[J]. 信号处理，2018，34（1）：81-88.

[20] 李汀. 多用户干扰信道下建模于流形上的联合干扰对齐预编码[J]. 数据采集与处理，2017，32（6）：1115-1124.

[21] ANMING D， HAIXIA Z， DONGFENG Y，et al. Interference Alignment Transceiver Design by Minimizing the Maximum Mean Square Error for MIMO Interfering Broadcast Channel[J]. IEEE Transactions on Vehicular Technology， 2016， 65（8）：6024-6037.

[22] VASILIS N，MOHAMMAD A，GIUSEPPE C. Cellular Interference Alignment[J]. ?IEEE Trans. Inf. Theory， 2015， 61（3）：1194-1217.

[23] RAZAVI S M， RATNARAJAH T. Adaptive LS and MMSE based beamformer design for multiuser MIMO interference channels[J]. IEEE Transactions on Vehicular Technology，2016，65（1）：132-144.

[24] AQUILINA P， RATNARAJAH T. Performance analysis of IA techniques in MIMO IBC with imperfect CSI[J]. IEEE Communications Magazine， 2015， 63（4）： 1259-1270.

[25] RAZAVI S M. Unitary beamformer designs for MIMO interference broadcast channels[J]. IEEE Transactions on Signal Process，2016， 64（8）：2090 -2102.

（责任编辑：孙娟）

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。