《交叉立方体连通圈网络的Hamilton分解》-工学论文，软件工程论文-论文范文参考-科学狗论文网

标题

交叉立方体连通圈网络的Hamilton分解

范文

张欣++师海忠

摘要：交叉立方体连通圈网络CQCC（n）（n≥3）是一类典型的互连网络，它是3正则的，在2010年，师海忠提出如下猜想：CQCC（n）（n≥3）是Hamilton可分解的，也就是说，交叉立方体连通圈网络CQCC（n）（n≥3）可分解为边不交的一个Hamilton圈和一个完美对集的并，在这篇文章中，证明了当n=3；4；5；6时猜想成立，即交叉立方体连通圈网络CQCC（n）（n=3；4；5；6）可分解为边不交的一个Hamilton圈和一个完美对集的并。

关键词：互连网络；交叉立方体连通圈网络；Hamilton圈；完美对集

中图分类号：PT393

文献标识码：A

DOI：10.3969/j.issn.1003-6970.2015.08.020

0 引言

超级计算机为实现高性能计算提供了硬件支持，为了满足对计算能力日益增长的需求，需要设计出更好性能的超级计算机。互连网络是超级计算机的重要组成部分，互连网络的性能在很大程度上决定超级计算机的性能。互连网络常常模型化为一个无向图，顶点对应处理机，边对应通信链路。在文献[12-15]中设计出了具有小的固定的度（为3）的多种互连网络。受细胞分裂生长过程的启发，在文献[16]中，提出了互连网络的细胞分裂结构图模型，在文献[15； 17-18]中研究了多种互联网络的Hamilton分解。

在文献[15]中，师海忠设计出了一类互连网络l{交叉立方体连通圈网络CQCC（n）（n≥3），也就是用连通圈替代交叉超立方体网络中的结点设计出的网络，改进了交叉超立方体网络的度随着其规模（顶点个数）的增大而增大的缺点。交叉立方体连通圈网络具有小的固定的度（为3）这一良好的性质，并且CQCC（n）的顶点数为n·2n个。

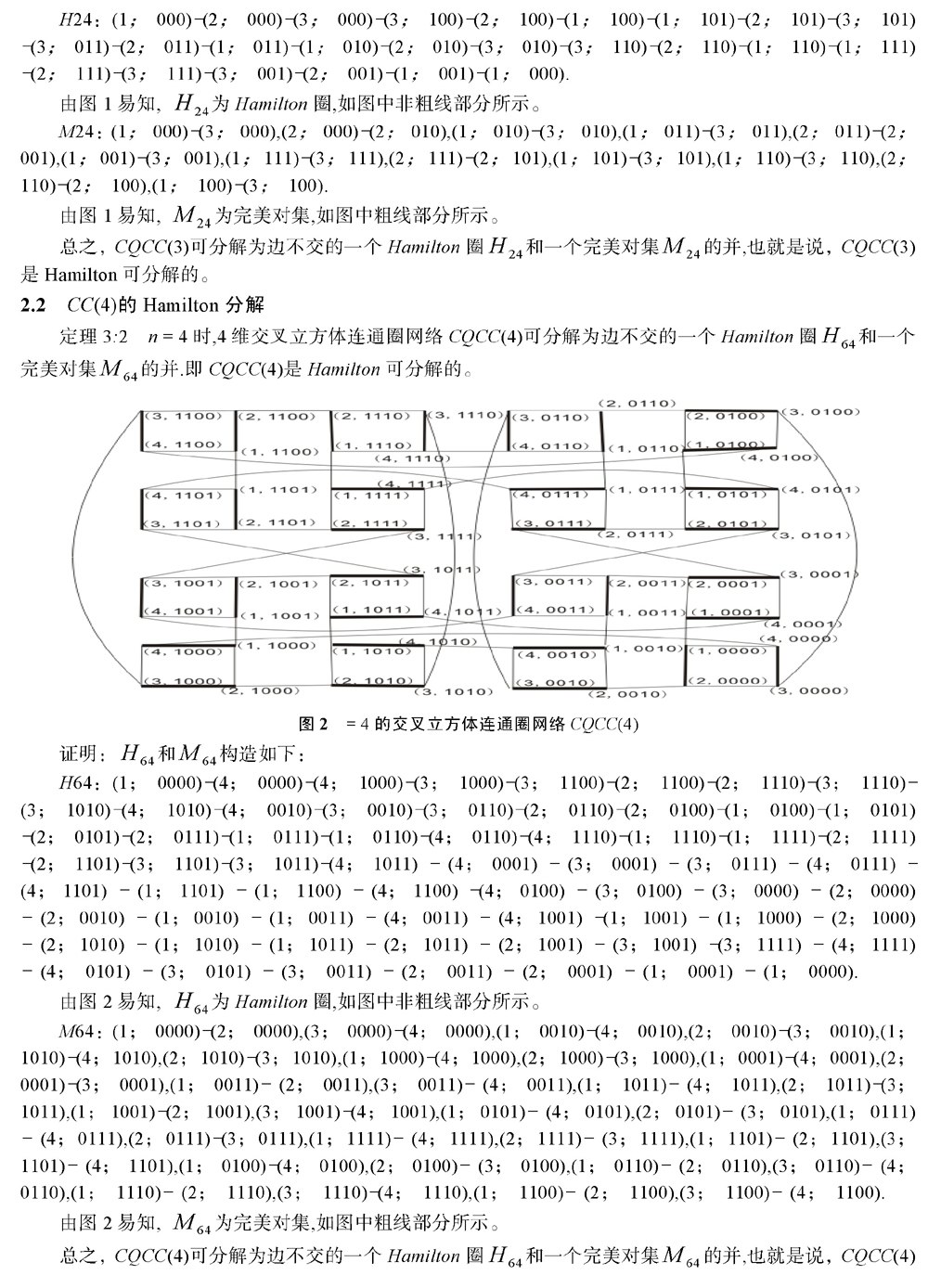
交叉立方体连通圈网络CQCC（n）（n≥3）是3正则的，在文献[15]中师海忠提出如下猜想：交叉立方体连通圈网络CQCC（n）（n≥3）可分解为边不交的一个Hamilton圈和一个完美对集的并，在本文中给出了交叉立方体连通圈网络CQCC（n）（n≥3）当n=3；4；5；6时的Hamilton圈和相应的完美对集，也就是说，对n=3；4；5；6猜想成立。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。