《基于混合遗传算法的无线回传网络部署》-工学论文，软件工程论文-论文范文参考-科学狗论文网

标题

基于混合遗传算法的无线回传网络部署

范文

张然++温向明++路兆铭

摘要：随着移动通信终端的爆发式增长和异构蜂窝网络的发展，无线回传网络的部署面临着越来越多的挑战。本文提出一种全新的小区内无线回传部署模型，该模型同时考虑回传网络的可靠性和小区内的能耗。通过混合遗传算法（hybrid Generic Algorithm）对该模型进行求解，得到最优化的回传网络部署方案。仿真结果表明，本文所提的算法与其他算法相比具有较为明显的优势。

关键词：通信与信息系统；可靠性；无线回传网络；混合遗传算法

中图分类号：TP393

文献标识码：A

DOI：10.3969/j.issn.1003-6970.2015.12.006

本文著录格式：张然，温向明，路兆铭.基于混合遗传算法的无线回传网络部署[J].软件，2015，36（12）：25-300

引言

21世纪以来随着通信技术的不断发展，社会经济发展水平与人们的生活品质也在不断提高。据全球移动通信系统联盟（GSMA，Global System forMobile Communications Alliance）报告，到2020年移动互联网用户总数将达到38亿，大约占据未来一半的全球人口。智能手机、平板电脑等终端的快速普及也带来了数量庞大的用户群体，随着接入终端以及业务类型的增加，为了尽可能的覆盖所有用户对象并保障网络性能，需要在小区中实现异构蜂窝网络的部署。异构蜂窝网络的关键思想是在宏基站小区覆盖范围内加入多个低发射功率小基站，这些基站拥有较小的发射功率和物理大小，通过这种方式可以增加一个地区的小区数，提高单位面积的频谱效率，这样就增加了蜂窝网络的系统容量，并且降低了宏基站的负载。当前无线业务需求以指数快速增长，这就要求了蜂窝系统的不断扩容。宏基站较大的发射功率和物理大小以及能安装的地理位置限制，导致存在一些地理区域的信号强度很小，甚至出现中断。各种小基站的覆盖和扩展能够以非常低的成本完成对整个区域的无缝覆盖。

日益增多的小基站给用户带来更加完善接入，同时也带来另外的问题。大量小基站的密集部署，使得连接基站和核心网的移动回传网络结构趋于多层次和复杂化。如何连接小基站到核心网以及蜂窝小区回传网络部署的目标是什么，这些都是在异构蜂窝网络规划中首先要考虑的问题。移动回传网络作为移动网络中重要的组成，一旦失效或者故障将会影响大量用户的正常通信。因此在研究未来小基站密集部署的环境下，如何对无线回传网络的部署进行合理规划具有重要的研究意义。这类网络规划问题一般从保障可靠性的规划目标出发，通常这类网络规划都规约为NP-complete问题。因此，设计出高效的网络规划算法是问题的关键。本文提出一种全新的以可靠性和能效为规划目标的网络规划模型。下面详细描述所提出的问题，并在后续的仿真中将所提遗传算法与其他可行的算法进行对比研究。

1 系统模型

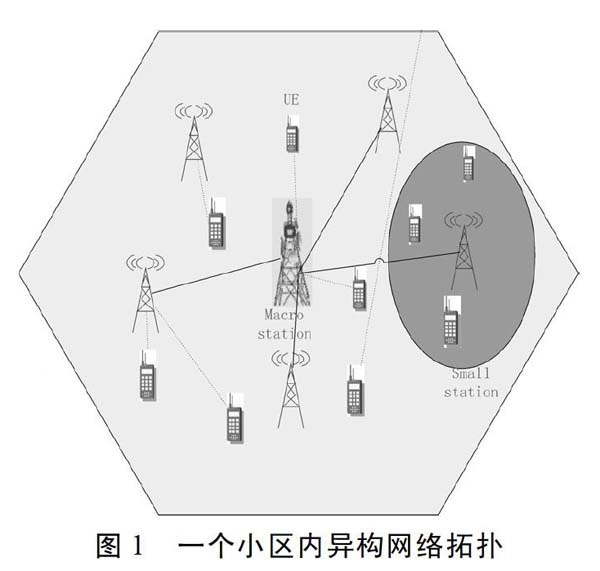
回传网络的连接方式一般有有线光纤连接和毫米波、微波无线连接方式，本问题的场景图如Fig.2所示，宏基站利用光纤实现有线回传，小基站与宏基站之间利用无线回传方式连接。在一个宏基站小区内的无线回传网络定义为有向图G=（V，E），其中包括有光纤回程的宏基站（编号为0），还有n个通过无线链路回程的小基站（编号为1，2，…，n，组成点集U）。整个宏基站小区拓扑的邻接矩阵为[bij]（n+1）×（n+1）。这里假设回传网络拓扑的形式为树形结构，这也是回传网络最常见的拓扑结构。

2 遗传算法概述

遗传算法是20世纪70年代由密歇根大学的John Holland提出的，它的主要思想基于达尔文的适者生存，可以把遗传算法看做生物的进化过程，首先对问题所求的解进行编码，这些编码即是个体的染色体基因，将求解空间表示成由各种染色体个体组成的种群。针对种群进行一系列自然选择，交叉，变异操作，经过一代代的进化，逐步提高种群个体的适应值，最终获得符合要求的解。

2.1 遗传算法的求解流程

2.1.1 问题解的编码

编码是设计遗传算法的第一步，也是极为重要的一步。在应用过程中，编码方式大致可分为三类：二进制编码，浮点数编码，符号编码。在本文的问题中，采用符号编码方式获得较低维度的解编码。

2.1.2 适应度函数

遗传算法搜索就是根据适应度函数值来对染色体进行评估。在很多遗传算子的操作中会用到适应度值。适应度函数通常都是算法的目标函数，或者与目标函数有关。适应度函数值愈大表示该个体的适应程度愈好，被遗传到下一代的可能性更高。

2.1.3 遗传算子

遗传操作通常有三种：选择，交叉，变异。通过这三种算子的操作保证进化的下一代的个体携带更加优良的基因编码，更加接近问题的最优解。具体的操作过程如下所述：

（l）选择算子

选择算子体现进化过程中自然选择的特点，把当前代种群的优秀个体保存到下一代中。同时，淘汰了种群中适应度差的个体，选择算子根据适应度函数值执行选择操作。以下是经常用到的选择算子操作方法：

轮盘赌算法，该方法求出个体与所有个体适应

最佳个体保存法，这种方法将群体中适应度高的个体直接保存到下一代种群中，这样操作可以保证交叉和变异不会破坏适应函数值较高的个体。

（2）交叉算子

交叉算子是指把父代个体的染色体对应的基因进行交换或者覆盖操作以便获取基因重组，然后能获得子代的新的染色体。单点交叉是常见的交叉算子，当使用二进制编码时，单点交叉操作如下图所示：

（3）变异算子

变异算子在遗传算法中相当重要。前面提及的交义算子的丰要作用是用来牛成新的子代个体，这样交义算子可以保证遗传算法在整个种群中的搜索能力。当采用二进制编码时，其具体操作如下图所示：

2.1.4 终止条件

遗传算法需要预先设定终止条件来判断进化过程是否结束。终止条件可以可以设定为种群的平均适应度值或者最优的适应度函数值的变化幅度，例如0.01，0.001等，也可以设定为种群的最大进化代数。

3 无线回传网络部署问题的遗传算法设计

遗传算法可以有效地解决大部分最优化问题，但是在某些情况下，标准的遗传算法容易出现早熟，局部搜索能力差等问题。在上述模型中，约束条件首先要求保证所有解对应的是树形拓扑，并且含有树的度约束和高度约束条件，还要符合发射功率的限制条件。这些的约束条件对于遗传算法的应用带来了很大的挑战，如何合理处理约束条件，在可行解域提高搜索效率并且保证搜索的健壮性是求解这个问题的关键。有些学者提出了混合遗传算法，比如将爬山法，模拟退火算法等加入到遗传算法的某一步骤中，这种与遗传算法的互补结合来解决约束条件显示出比标准遗传算法更优越的性能。

3.1 基于Prufer的编码

Cayley定理告诉我们有n个顶点的完全图，它的生成树有nn-1个。Prufer对n-2个l～n的数的排列与树的一一对应关系给出了结构化的证明。每一组Prufer数都对应着独一无二的一棵树。因此，再进行交叉，变异这些遗传算子操作时，所得到的还是一棵树，在不考虑其他约束条件（例如，度的限制，高度的限制等）不会产生不可行解。

从树到Prufer的编码过程如下：

Stepl）对树T的n个节点进行编码

Step2）选择树T中编号最小的叶子节点i，写出与它相连的节点j.把j的编号作为编码的第一位，这里是从左往右进行编码

Step3）删除节点i以及与i相连的边

Step4）重复上述操作直到只有一条边为止

从以上树T的Prufer数（编码）知，树T中顶点i的度等于i在树T的Prufer数中出现的次数加一。下图是一个编码Prufer数的例子，这棵树T所对于的Prufer数P=（66551）。首先顶点2是最小的叶子，顶点6和2相连，这样6是Prufer数中第一个数；然后从T中删除点2和边（2，6），重复这一过程直到剩下边（l，7）

从Prufer到树的解码过程：

Step l）P是原始的Prufer序列码，是没有出现在Prufer序列码中的节点的集合。

Step 2）假设j是中编号最小所对应的节点，k是P中最左边编号所对应的节点，将j和k相连，并将其在所在集合中删去。重复操作直到P集合中没有编码。

Step 3）如果没有编码在P集合中，应该在中还有两个点集r和s，并将r和s相连接，这样就构成了n-l条边的树。

运用以上的步骤将Prufer数P=（6 6 5 5 1）解码成上图的一棵树。因为顶点2，3，4和7不包括在P中，因此=（2 3 4 7），注意到中最小的数字是2，P中最左边的数字是6，因而把变（2，6）添加到树中。同时从中删除点2，P中删除6，这样剩下的P=（6 5 5 1），=（3 4 7）。重复以上过程直到P为空，最好把中剩余的1和7作为边（1，7）加到树中就构成了上图。

3.2 适应度函数

遗传算法求解非约束型问题的求解应用广泛，但是对于本文问题中的约束条件处理存在一定的难度。等式约束条件由于编码方式的选择已经得到了保证，关键在于不等式约束条件的处理，常见的对约束条件的处理，有罚函数法，对不可行解的拒绝策略，对遗传算子进行改进从而将不可行解转变为可行解。通常采用罚函数的方法，该方法将背离约束条件的程度用罚函数来表示，将其加到适应度函数后面，从而将有约束问题转化为无约束问题。在本章所提的模型当中，约束条件（4）（5）（6）有很多，而且树形拓扑的约束条件很难选择合适的罚函数对约束背离程度进行合理的度量，这也是罚函数法处理多约束最优化问题的局限性。第一种方式，对不可行解的拒绝策略等减少了种群的多样性，这样不利于算法的全局搜索，容易出现早熟现象。第二种处理方式，改进算子增加了算法的不确定性，而且改进算子的单一化也容易导致算法搜索方向的单一性。为了将遗传算法合理地应用到本章的问题当中，结合模拟退火算法，提出一种退火函数，将其添加到适应度函数当中，通过模拟退火方式来自动调节不可行解的惩罚，这是一种混合遗传算法。

模拟退火借用了统计力学的思想，目标函数类比于系统的内能E，引入参考温度T。初始化时，令T取一个较大的值，如果AEO，则以概率

随着种群个体的不断更新演进，退火温度呈几何级数降低，最终导致不符合约束条件的解将被舍弃。同时，当算法刚开始执行时，为了保证种群的多样性，不舍弃但是具有潜力的不可行解，这些解将会参与种群的演进过程而被充分利用。这样的做法，即处理了数量较多的约束条件，又保证了种群的多样性，防止陷入局部最优解当中。

本问题算法过程如下：

4 仿真分析

4.1 仿真环境和参数配置

问题的仿真环境是基于MATLAB 2013a，运行在Pentium 4 CPU，4GB内存的PC机上，算法采用了MATLAB中的遗传算法工具箱。

4.2 仿真结果分析

本文将所提算法的通过与其他算法（分支定界，粒子群）对比，得到下面的仿真结果图：上图描述了采用不同算法的情况下，小区内无线回传网络平均吞吐量（Throughp ut Expectation）与小区内基站部署数目之间的关系。从图中可以看出，平均吞吐量（Throughput Expectation）随着小区内的基站数目呈明显的增加趋势。此外，通过三种算法的对比，可以明显看出本文采用的算法所部属的网络总的功耗（Throughput Expectation）更大，优于其他的两种算法（分支边界、粒子群）。

在上图中，随着小区内的基站数目的增加，小区总的能效（Energy Efficiency）也在增加，这也说明大规模部署小基站带来提高小区内的能效这一显著的优势。另一方面，与其他两种算法相比，本文所提算法能够能效更高，具有更明显的优势。

5 结论

本文给出了一种基于混合遗传算法（hybridgenetic algorithin）的无线回传网络部署方法。在获得基站各项参数和信道传播特性的条件下，建立无线回传网络部署的0-1整数规划模型，将问题转化为搜索0-1整数空间的最优解。针对所建立模型的特点，提出了一种新型的遗传算法，通过该算法，模型解空间中原先的0-1编码变为基于Prufer的编码，大大减少了最优解搜索的难度，同时利用模拟退火解决解对约束条件的满足问题，进而得出了符合收敛条件的近似最优解。为了验证算法的性能，搭建仿真环境进行了实验。实验表明本文所提算法在无线回传网络部署中，可以明显提高小区内回传网络的可靠性，同时也保障了回传网络可靠性与小区能耗之间的平衡。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。