《基于Adams的三自由度Delta机械手的运动学仿真分析》-工学论文，软件工程论文-论文范文参考-科学狗论文网

标题

基于Adams的三自由度Delta机械手的运动学仿真分析

范文

伍经纹+徐世许+王鹏+宋婷婷

引言

机器人技术发展给传统的工业带来了巨大的变化，大大的提高了社会生产力水平。现代工业生产中运用的工业机器人大致可以分为串联工业机器人和并联工业机器人和混联工业机器人。最典型的并联机器人是Delta机器人，它是由R.Clavel博士于1985年提出的。其中，三自由度的Delta并联机械手具有刚度大，承载能力强、重量轻、体积小、定位精确、效率高等特点，在包装、分拣、轻量搬运等生产工序中得到广泛应用。现如今为适应越来越苛刻的产品质量要求，大幅度提高企业效率，国内外各大机器人制造厂商分别制造出各自的Delta机器人。Delta并联机器人呈现出高速高精、灵活性等方向的发展趋势[。但值得指出的是，尽管近些年来不断涌现出结构特点鲜明的并联机器人样机，但与串联机构的产业化水平相比，并联机械手还存在较大差距。究其根本原因，控制层面研究成果的缺乏很大程度上影响了并联机械手的工作性能，阻碍和限制了该类机械手在工业中的前景。目前对Delta机械手在轨迹规划、控制策略方面还不够成熟导致机械手运动過程出现剧烈震动，使得机械手的使用寿命降低，增加企业成本。通过对运动轨迹和路径合理规划，可以提高机械手的效率、稳定性、可靠性，延长使用的寿命。因此本文采用改进修正梯形加速度的方法在笛卡尔坐标系下进行轨迹规划、采用虚拟样机ADAMS软件进行运动仿真获得结论。

1Delta机械手运动学

1.1Delta机械手的数学模型

Delta机械手有三个平动自由度，建立数学模型如图1所示，分别以等边三角形AClC2C3中心O和AAlA2A3中心0建立静平台坐标系O-XYZ和动平台坐标系o-xyz。其中，x轴沿着主动臂C1B1方向建立，z轴与静平台垂直并指向上，Y轴的方向根据右手定则确定。动平台坐标系的建立同理。机械手的主要参数有主动臂长度，从动臂长度为，静平台外接圆半径为R，即动平台外接圆半径为相互之间夹角为e=120°，静平台与主动臂之间的夹角。对于并联机器人，位置逆解即为已知机构末端运动位置情况下，求解主动臂所需转动的角度。

1.2 Delta机械手逆解分析

根据1.1小节建立的静平台坐标系，获得静平台与主动臂之间关节Ci位置矢量为：

最终根据机械手的末端位置坐标（x，y，z）可以获得主动臂转动角度即伺服电机驱动主动臂转过的角度e=2arctan。

2Delta机械手运动轨迹路径规划

2.1轨迹规划

机器人运动轨迹是指机器人在运动过程中的位移、速度、加速度。规划轨迹顾名思义就是按照任务要求，计算出运动轨迹。笛卡尔坐标系下轨迹规划是任务层规划，具有直观、便捷的优点，直接对机械手的位姿进行规划，但需要将笛卡尔空间的位姿转换为驱动臂转动角度，涉及大量的运动逆解。Delta机械手作为并联机器人逆解比较容易求解，1.2小节已给出。机械手轨迹规划的目的是给定位移和最大加速度的前提下，优化其末端执行器的运动轨迹，使运行时间和机械振动趋于最小。那么至少满足以下两个条件：末端执行器起始点和结束点速度、加速度都为零。位移对时间的一阶、二阶导数连续，且三阶导数有上界。张祥等人计算比较过，采用修正梯形加速度是在位移、最大加速度相同的情况下，运行周期最短，在整个轨迹过程中快速、平稳、没有刚性冲击。对修正梯形加速度曲线求导获得跃度曲线，会发现运行开始点和结束点附近存在跃度突变，这会带来柔性冲击，影响机械手运行稳定性。为了消除冲击，对修正梯形加以改进后的加速度表达式为：

如图2所示，将amax单位化后进行改进前后加速度对比，发现改进后加速度在运行的始末两端明显变的平缓。

对加速度积分得到速度变化曲线，对速度积分得到位移曲线，分别如图3，图4所示。

2.2路径规划

Delta机器手主要执行抓取和放置操作任务，机械手末端的运动路径一般采用“门”字形，如图5所示。P1作为起始点，P6作为目标点，机械手进行往复运动。以上升和下降阶段垂直距离为100 mm、水平阶段距离为400 mm为例，垂直阶段与水平阶段之间通过弧p2p3和弧P4P5代替突变的拐角。弧P2P3和弧P4P5是通过垂直运动和水平运动的时间耦合形成。以单个周期为例具体过程是当机械手末端运动从起始点P1开始竖直向上运动在t1时刻到达P2点启动水平运动，在T时刻从P3点开始变为完全水平运动，在（T-Tv）时刻从P4点启动竖直向下运动，在（T-t1）时刻从P5点到目标点P6为完全竖直向下运动。整个运行周期。

3Delta机械手的仿真分析

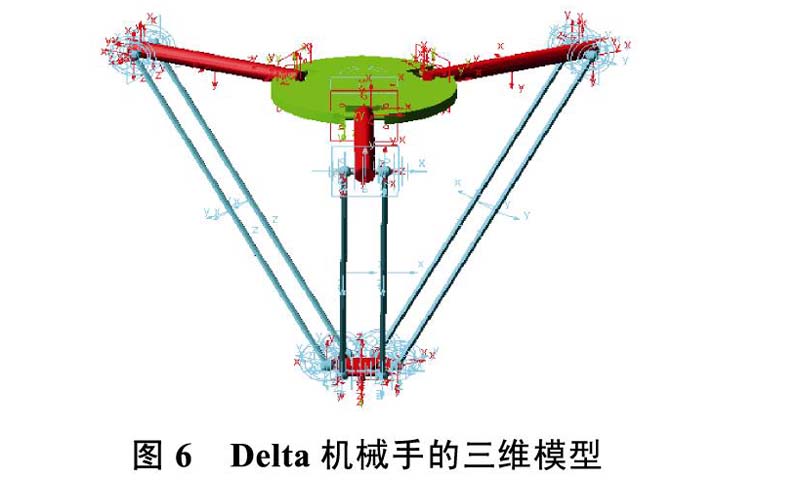
通过ADAMS软件建立Delta机械手的各零件的三维模型，然后进行装配得到完整的Delta机械手三维模型。如图6所示，简化Delta机械手机械结构，主要有静平台、动平台、主动臂、从动臂构成。其中静平台与主动臂之间通过旋转副联接，从动臂与主动臂、动平台与从动臂通过球副联接，通过ADAMS验证自由度为3，因此添加的约束副正确。

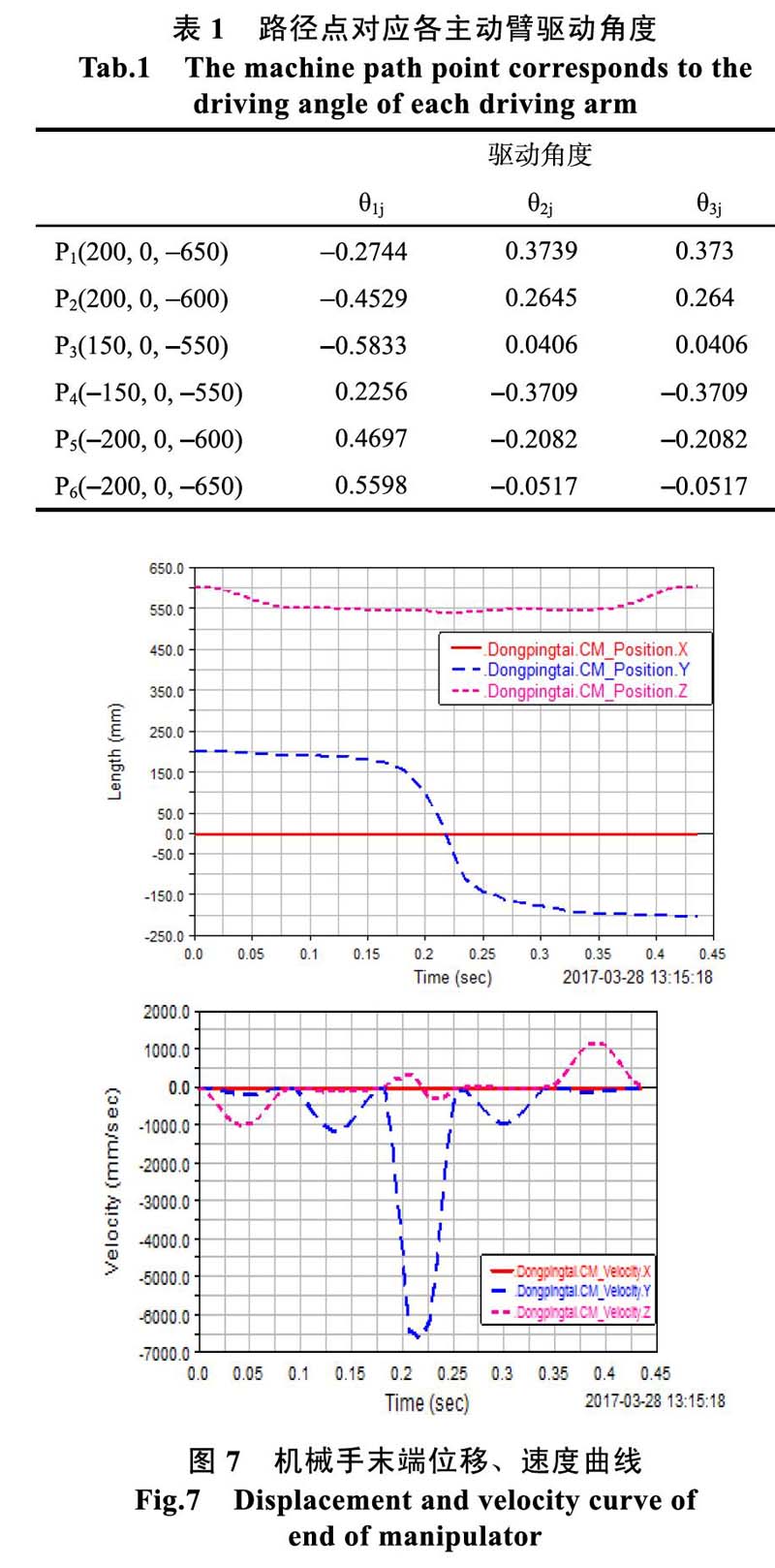
根据路径规划和给定的机器人结构参数，利用MATLAB软件编写反解算法求解机器人末端位置对应的主动臂驱动角度e（i=1，2，3），如表1所示。Delta机器人结构尺寸参数R=120 mm；1=45 mm；La=260 mm；Lb=640 mm；

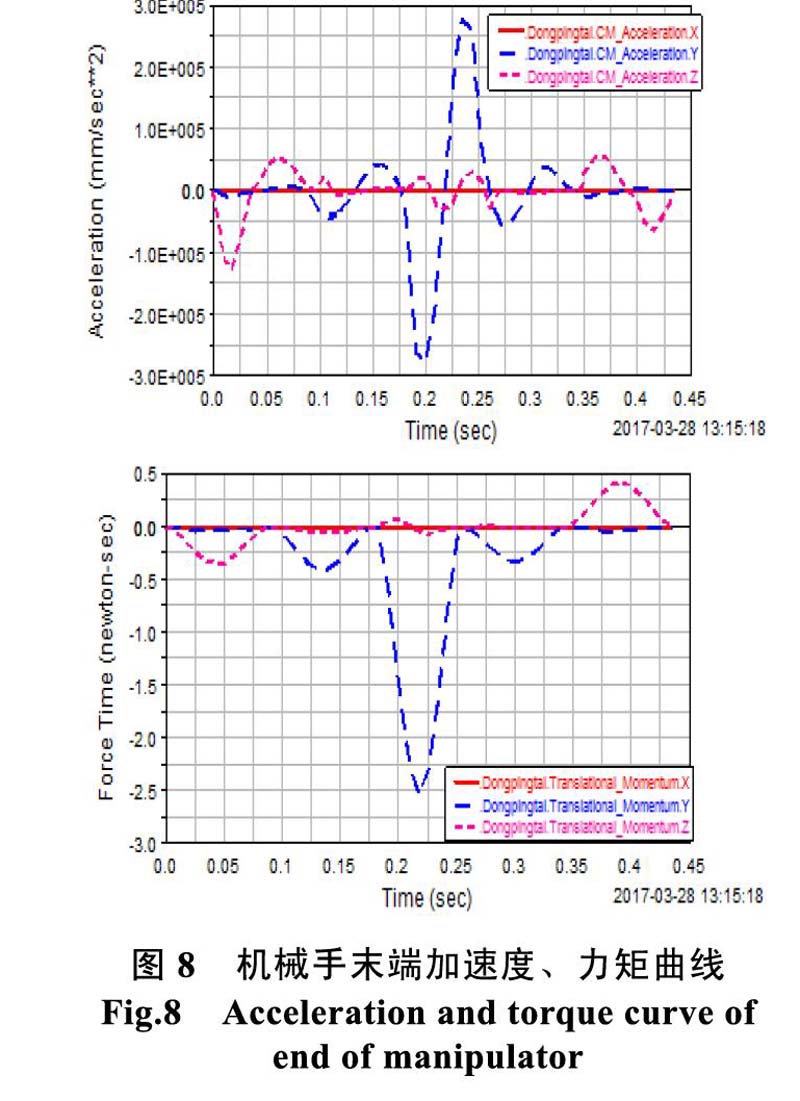
由2.2小节设定最大加速度、时间参数可以通过SPLINE工具将数据导人ADAMS三维模型的三个驱动MOTION中，驱动虚拟样机进动力学仿真。防真结束后通过ADAMS的结果后处理获得机械手末端的位移、速度、加速度和力矩曲线，初步达到了预期的轨迹规划如图7，图8所示。

4 结束语

针对三自由度Delta机械手在分拣、包装行业的广泛应用，对于机械手的理论研究显得尤为重要，本文首先建立Delta机器手的数学模型，给出机械手的逆解解析方程，为轨迹规划提供前提；其次，采用改进的修正梯形加速度曲线，消除运动始末端的给机械手带来的冲击。通过虚拟样机ADAMS搭建Delta样机平台将MATLAB计算出的时间与主动臂对应转角添加到主动臂获得机械手末端的运动参数，验证时间耦合规划的路径合理可行。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。