《基于AHP模糊综合评价法的孵化器有效运作因素研究》-工学论文，软件工程论文-论文范文参考-科学狗论文网

标题

基于AHP模糊综合评价法的孵化器有效运作因素研究

范文

熊刚+张星佳丽+商秀芹+Timo+R．Nyberg+刘陶忠

摘要：根據美国企业孵化协会（ NBIA）给出的定义，孵化器是通过对新创企业提供创业指导和所需资源及服务，以加速其成功发展的商业支持过程集合体。本文首先从有效孵化相关的功能角度，筛选出孵化器的有效运作因素，然后采用层次分析法对于调查数据进行了计算，得到了各个指标的权重。利用模糊综合分析法对于影响孵化器有效运作因素进行了判定。最后对某地多个孵化器进行了实证分析。分析结果显示，孵化器运作良好。

关键词：孵化器；AHP模糊综合评价法；有效运作因素

0 引言

孵化器是整合社会资源并实现自己主创新成果产业化的重要载体，是国家创新体系的重要组成部分。经过二十多年的发展，中国孵化器的数量仅次于美国，居世界第二位。孵化器行业对创业企业成长的促进作用越来越引起社会关注。国家和地方政府为孵化器平台搭建相关的大数据服务平台，以辅助孵化器和在孵企业健康发展。

随着互联网快速发展所出现的虚拟孵化器，则是通过现代信息技术交流手段，以互联网为线上平台的新型孵化形式。这种符合信息时代特征的新型孵化方式，吸引了不少专家学者对于其定义与属性，发展模式以及合作规范等进行研究。

但是，我国孵化器行业在快速发展的同时，出现了很多问题。而在此之中的核心问题可归结为孵化器有效运作因素的研究。当前我国学者对孵化器的研究，主要涉及孵化器的核心竞争力、盈利能力、与风险投资融合的经营模式，也有关于孵化器的管理绩效评价以及相关指标体系等问题，但对孵化器有效运作因素尚未有系统完善的评估。陈芝等对于现有的指标体系进行分类，增加了企业孵化器自身发展相关的权重参数。张礼建等构造了科技企业孵化器孵化绩效评价指标体系。晏敬东等针对科技企业孵化管理绩效建立了评价指标体系。

本文基于科技创新企业孵化器有效运作的关键因素分析，建立评估孵化器的一个指标体系，同时利用AHP-模糊综合评价法对于孵化器进行评估，确定各项影响因素在孵化器运作中所占的权重，将各项指标因素的权重以量化表格形式显示，一目了然的显示各项指标在运作之中的权重。最终的权重数据，对于政府、企业在进行科技创新产业孵化器管理时有很好的指导作用，从而更好的发挥孵化器对于创业的激励作用。

1 模糊综合评估模型的建立

模糊综合评价的基本步骤：首先依据评估对象确立合理完善的评价指标体系，通过层次分析法确定各个评价因素的权重。然后根据评价的要求，设定合适的评价集，并确立评价因素的隶属度函数，最后进行模糊综合评判。

1.1 建立评价指标体系

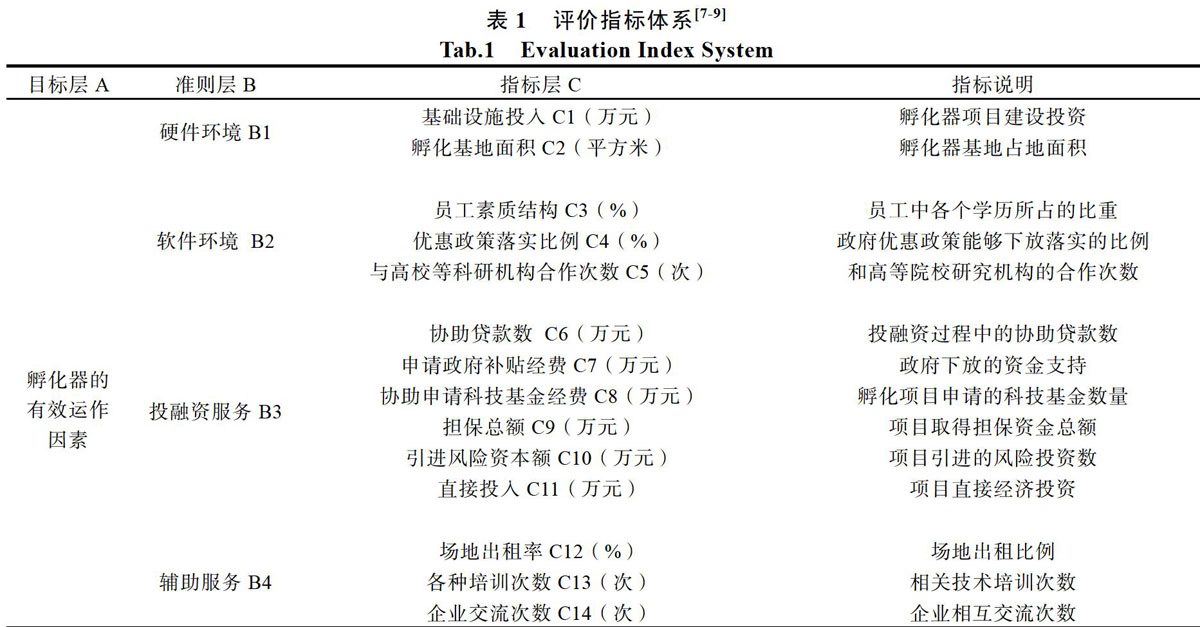
评价科技企业孵化器，需要建立合理且全面的评价指标体系。首先，就是掌握影响科技企业孵化器有效运作的各种因素，要把影响其运作流程的各种复杂成分简单化，明确主要因素和次要因素。其次，建立科技企业孵化器评价模型，还需要逐一了解孵化器孵化流程中各个环节的实施状况，为分析影响其有效运作的因素创造条件。结合相关文献资料分析，我们采取从孵化器硬件环境、软件环境以及孵化器服务能力等几个方面，建立孵化器有效运作因素指标体系：

（1）孵化器硬件环境：是指由客观环境所决定的，影响孵化器进行进一步发展的硬件限制因素；

（2）孵化器软件环境：是由孵化器中人才引进以及交互交流带来影响的软性指标；

（3）孵化器投融资能力：反应孵化器经济功能；

（4）孵化器辅助服务能力：反应孵化器服务社会功能。

我们所建立的科技企业孵化器有效运作的指标体系，如表1所示。

1.2 科技企业孵化器指标体系的计算

每个准则?Vi（i =1，2，3，4），综合反映若干个大类指标Vij（j =1，2，…，m），例如：孵化器硬件环境因素K，是由孵化器基础设施投入V以及孵化器基地共同决定的，即对于V，均有：

其中，i=1，2，3，4；j=1，2，…，m，m为所有因素（V1，V2，V3，V4）中大类指标数的最大值。据此，就构建了科技企业孵化器有效运行指标体系。它分为2个层次，第1层次，准则层，影响孵化器有效运作的4个准则，第2层，具体指标层Vij决定准则层各准则的综合指标。这里，W=1，2，3，4；j=1，2，3，…，m）是权重，权重反映了指标对所影响的对象的重要程度。我们采用层次分析法确定各个指标的权重。

1.3层次分析法确定指标权重

层次分析法的基本思想是将想要达到的总目标进行量化分解成多个不同的组成因素，并按照因素间的相互关联影响以及隶属关系将这些组成因素按不同层次聚集组合。形成一个多层次的分析结构模型，从而最终使问题归结为最低层（供决策的方案措施等）相对于最高层（总目标）的相对重要权值的确定或相对优劣次序的排定。

运用层次分析法解决决策问题一般分为五步：建立层次结构模型；构造判断矩阵：层次单排序及一致性检验；层次总排序；层次总排序一致性检验。按照层次分析法的步骤，已确定指标体系和划分层次结构这两个步骤，这套评价指标由两级指标组成，所以必须先求出第一级指标的权重，再求第二级指标的权重；

1.3.1 构造判断矩阵A

判断矩阵是层次分析法的基本信息，也是进行相对重要度计算的重要依据。层次分析法的信息基础，主要是人们对于每一层次中各因素相对重要性的判断这些判断通过引入合适的标度，用数值表示出来，写成判断矩阵。判断矩阵表示针对上一层次某因素，本层次与其有关因素的相对重要性的比较。例如，某上一级因素HS有n个下级独立要素A1，A2，…，An。，其判断矩阵形式见下表2。

判断矩阵中的元素a表示从判断准则E。的角度考虑要素ai，对要素aj，的相对重要性aij=wi/Wj

1.3.2 判断尺度

表示要素ai，对要素aj，的相对重要性的数量尺度。表3是一种常用的1-9判断尺度表。

1.3.3 运用方根法求解判断矩阵

在单一目标层A下被比较元素的相对权重，即层次单排序，计算步骤如下：

（1）权重向量的近似计算

计算判断矩阵每一行元素的乘积：

计算Mi的n次方根：

对Mi的标准化：

（2）最大特征根的计算

采用公式（4）求取判断矩阵的最大特征根 λmax用于一致性检验。

其中w是用根法求出的权重向量。

（3）将所得的W向量做归一化处理，得到单一准则下各被比较元素的排序权重向量。

一致性检验的基本步骤：基于公式（5）得到判断矩阵的最大特征值，然后代入公式（6）和（7）中，计算判断矩阵的一致性指标CI和一致性比CR。

式中，4是A-B判断矩阵，n是判断矩阵阶数， λmax是判断矩阵最大特征值。CI数值越小，就说明判断矩阵一致性越高。单纯依据CI值设定一个可接受的不一致性标准，并不恰当。因此，进行一致性检验前，需要排除判断矩阵不同阶数对指标判断的影响。

平均随机一致性指标RI，就是一种修正系数，可消除由矩阵阶数因素所造成的判断矩阵不一致性。具体数值如表4所示：

对于n>3阶的判断矩阵，当CR≤0.1时，即λ max偏离n的相对误差。当RI不超过平均随机一致性指标Ci的0.1倍时，则可认为判断矩阵一致性是可接受的。当CR> 0.1时，则可认为判断矩阵偏离一致性程度过大，需要调整判断矩阵，直到达到满意的一致性为止。

1.4确定评语集和隶属度函数

单因素评价和建立评价矩阵时，可将评价等级分为优、良、差三个等级，建立评价等级集V=[优，良，差]。

1.5单因素评价和评价矩阵建立

从一个因素出发进行单独评价，以确定评价对象对于评价集元素的隶属程度，称为单因素模糊评价。假设对第i个评价元素μi，进行单因素评价，得到一个关于Vi的模糊向量：

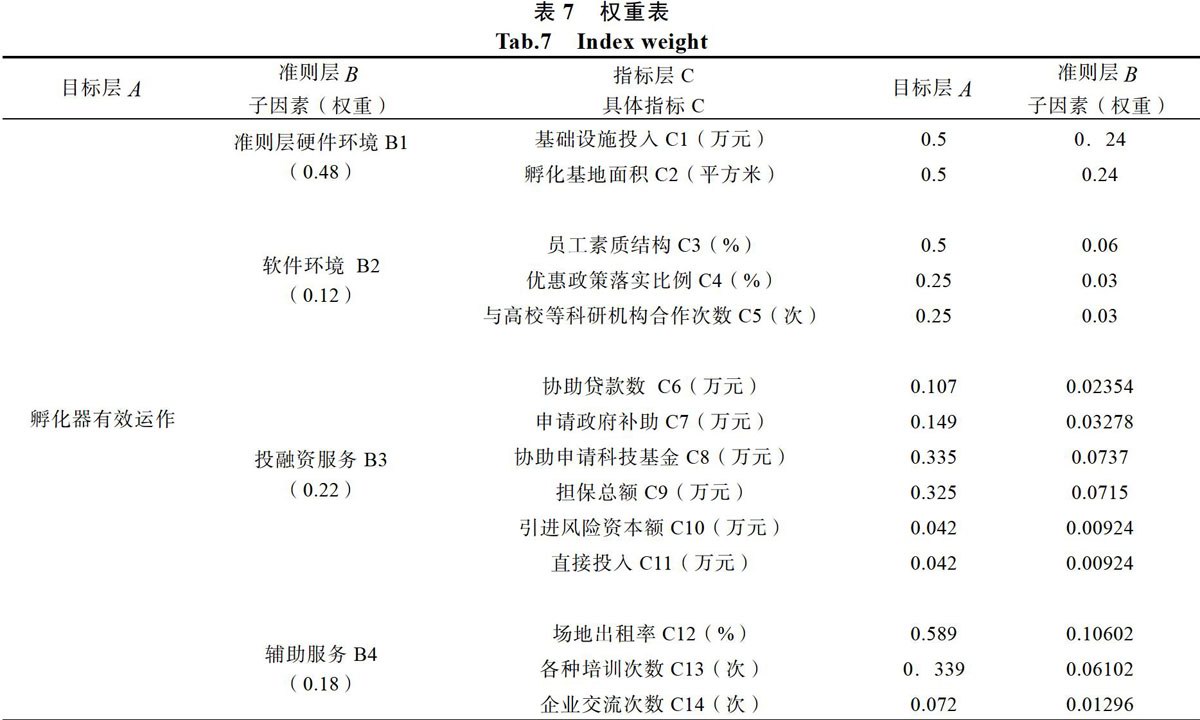
riji，具有vj，的程度，0

1.6 进行模糊合成和评价

本文选择加权平均算子，进行模糊合成。应用不同的模糊算子，对二级指标进行模糊合成，会演变出不同的模型。

2 某地孵化器平台有效运作评估案例

2.1 权重的确定

2 .1.1 构造判断矩阵

AHP的判断矩阵分布权重，通过专家组对各级评阶中的各个元素重要性进行两两比较与量化评价获得。专家量化评价结果采用1～9的标度法，分别考察B层因素和C层因素的相对重要性，可以得到A-B、B-C判断矩阵。结果如下表5所示：

2.1.2 求解判断矩阵

（1）权值的近似计算

由公式（1）计算图1中每行元素的乘积，得到：

由公式（2）得到各个项的四次方根：

μ1=2.21 μ2=0.54 μ3=1 μ4=0.84

由公式（3）进行标准化得到：

w1=0.482 w2=0.117

w3= 0.218 w4=0.183

由此，得到特征根：

（2）最大特征根的计算

由公式（4）计算得：

2.1.3 一致性检测

由公式（5）（6）（7）知，一致性检测中各项参数如下：

同理，可以求出权重表，如表6，表7所示。

2.2 进行综合模糊计算

2.2.1 建立评价矩阵

对于定性指标，采用专家打分法获得评语集。对于定量指标，采用隶属度函数进行模糊评价，如表8所示。

2.2.2 确定权向量

由本文2.1小节中，利用AHP层次分析法得到了指标层C相对于准则层B以及目标层A的权重，如表6所示。

2.2.3 一级评价

根据公式Bi=Wi×Ri得到B层各个指标模糊计算结果，如表9所示。

2.2.4 二级评价

根据公式Bi=Wi×Ri，把Bi看做是A的4個单因素判断，则对目标层A的综合评价为：

B=W×R

w为A层各下级元素相对于A层的权重，可知：

W=[0.48 0.12 0.22 0.18]

R为模糊评价矩阵，由一级评价知：

计算得：

B =[0.59

0.265

0.145]

2.2.5 综合评价

按照最大隶属度原则，我们对某地孵化器进行分析后结果显示，关于孵化器有效运作的诸多指标较好，我们认为该孵化器状态良好。通过该孵化器的有效运作因素评价过程，我们能够发现孵化器在运行中出现的问题来源，量化的评价，也可以方便对于相似孵化环境的孵化器进行孵化指标判断。从层次分析法得到的量化指标权重中，在政府部门建设和管理科技创新孵化器时，应当注重软硬件的基础投资。在此基础的保障下，孵化器才能更好为社会发展，科技进步提供支撑支持，更好地发挥孵化器的孵化作用。同时，针对不同的地域，不同经济状况，不同孵化条件和背景的孵化器，在进行评估时，应当考虑差异，结合时代对于孵化器孵化作用的要求，结合不同的背景特点，选取合适的指标，并进行合适的权重评价。

本实例计算中，我们首先对于某地孵化器按照表1中的相关判定指标进行了指标权重的评价，评价产生了相关的判断矩阵，并将得到的判断矩阵进行一致性检测。然后，根据收集的数据，对于相关评价指标进行模糊评价，建立了评价矩阵，计算相应的权重以及进行了综合评价。

3 结论

为满足科技企业孵化器评价工作不断完善的需求，需要加强孵化器有效运作因素研究，将其运作过程中所涉及的复杂关系简单化为主要因素和次要因素，并获取量化的指标信息，为准确把握其发展趋势并推动实现动态管理提供科学的判断依据。不断完善科技企业孵化器有效运作的评价指标体系，有助于发现孵化器运作过程中存在的不利因素和缺陷，分析原因并及时采取合理的应对措施。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。