网站首页  词典首页

请输入您要查询的论文：

　

标题 混凝土成层结构的流激振动特性
范文 牛超等



摘要：泄流激励引起水工建筑物振动的现象时有发生且形式多样，严重的还可能引起结构的破坏。对于混凝土成层结构而言，由振动引起破坏的案例不多，对其振动响应机制的研究也不够深入。以混凝土拱坝为例，通过数值计算及模型试验对比分析了整体与成层两种不同结构在相同泄流荷载作用下结构的振动响应，探讨了响应与结构自身的关系，并结合“拍”的概念，对混凝土成层结构振动响应特性与泄流荷载之间的关系进行了研究。结果表明，成层结构频率相近的前两阶振动是拍振形成的主要原因。此外，即使不满足拍振形成的条件，振动曲线同样可以表现为“拍”的形式，且振动量较受迫振动大幅增加，实质为“水力共振”现象。
关键词：泄流激励；成层结构；响应机制；拍振；水力共振
中图分类号：TV65 文献标志码：A 文章编号：1672-1683（2015）03-0476-06
Abstract：Vibration of hydraulic structures caused by flood discharge excitation occurs frequently and has different forms，and serious vibration may lead to structural damage.Few cases of damage caused by vibration for layered concrete structures were presented，and the study of vibration response mechanism was not enough.In this paper，the vibration responses of concrete arch dam with two different structures，including a whole structure and a layered structure，under the same flow discharge conditions were investigated through the comparative analysis of numerical calculation and model test.The relationship between the structure and vibration response was analyzed.Furthermore，the relationship between the vibration response of layered concrete structure and flow discharge was studied in consideration of the "beat" concept.The results showed that the beat vibration is mainly caused by the first two bands of vibration with similar frequency.Although the conditions for the formation of beat vibration may not exist，the vibration curve can present the form of "beat"，and the vibration quantity is much large than that of the forced vibration，which indicated that this is actually the hydraulic resonance phenomenon.
Key words：flow discharge excitation；layered structure；response mechanism；beat vibration；hydraulic resonance
泄流诱发水工结构振动是一种复杂的流固相互作用现象[1]。在水利水电工程中，由泄流引起水工建筑物振动的现象时有发生，且形式多种多样。在复杂的水流激励荷载作用下还有可能引起结构的剧烈振动，甚至破坏。1982年对乌江渡水电站进行原型观测时发现左岸滑雪道式溢洪道右导墙存在强烈的“拍振”现象，墙顶铁栏杆振动剧烈，泄流量越大振动越明显。1978年8月进一步观测时发现，在闸门全开时，导墙的最大双倍振幅达3.1 mm，左导墙也出现了上下贯通缝。经过专门处理，工程才得以安全运行，但花费巨大[2-3]。
巨大的坝身泄洪量，几千万乃至上亿瓦的泄洪功率，给泄洪消能以及水工建筑物的减振减蚀带来了巨大挑战。本文结合模型试验及数值计算，分析碾压混凝土成层结构在不同幅频特性泄流激励作用下的振动特性，及其在流激振动条件下的振动响应机制。
1 结构流激振动机理及拍振
1.1 结构流激振动机理
在泄流振动领域，德国学者Naudascher[5]归纳了四种流体诱发结构振动的形式，即：外部诱发、不稳定诱发、运动诱发、共振流体振子诱发。大量的原型观测成果表明，泄流结构流激振动主要是外部诱发的振动，高坝泄流振动、紊流脉动压力诱发的消力池导墙振动等均属于此类振动[5]。外部诱发的振动是由水流激励或压力脉动引起的，并不完全表现为系统的固有振动。其中最受关注的就是在接近水工建筑物固有频率的荷载作用下所引起的结构振动[3]。
泄流结构若出现如图1中所示的振动情况，结构振动强度加剧，在该水流激励长期作用下结构易出现疲劳破坏。图1中所示的形如“拍”的拱冠梁振动现象称为“拍振”[6]。
2 混凝土成层结构的有限元模拟
当两个分离的表面互相接触并共切时，称其为接触状态。本文拟采用接触单元来模拟碾压混凝土成层结构的层间结合面，下面通过一组试验及有限元计算结果来验证其合理性。
2.1 参数设置及建模
本文以某导墙为例，分别采用数值计算和模型试验[13-15]的方法对混凝土成层结构进行模拟。模型采用加重橡胶制作，层间结合面采用南大703胶粘接，有限元模型中层间结合面采用接触单元模拟。
导墙尺寸为：墙高30.4 m，墙厚3.2 m，墙体长度79.2 m。混凝土参数为：弹性模量Ec=8.4 GPa（考虑到现有的加重橡胶弹模为105 MPa，按照λL=1∶80比尺转换），重度γc=24 000 KN/m3，泊松比为0.167。层间结合面采用接触单元模拟，用Targe170与Conta174分别模拟目标面与接触面，接触方式为不分离，罚刚度取0.3，其余实常数取合适值。
地基弹模取值对导墙低阶振动影响不大，当基础弹模大于11 GPa时，低阶振型频率误差在2%以内，高阶振型频率误差在3%以内，基本可以接受。故基础弹模取11 GPa，与导墙混凝土相当。
导墙左右两侧基础各取15 m，基础深度取10 m，上下游方向不做延伸。墙体和基岩分别采用Solid65和Solid45单元，模型底部采用固定约束，基础四周边界采用法向约束，有限元模型见图5。
2.2 动力分析
首先，利用ANSYS对导墙有限元模型进行动力分析，提取1号-6号测点动应力时程，与模型试验对应测点的动应力对比分析，均方差见表1。
3 流激振动条件下结构振动响应机理
为搞清混凝土成层结构-泄流荷载-振动响应三者之间的关系，本文采用某水电站混凝土拱坝模型开展研究。分析在不同频谱特性泄流荷载作用下，混凝土成层结构和整体结构的振动响应。整体及成层结构的前六阶频率（干模态）见表2。
根据式（7）所示的拍振形成条件及坝体前两阶振动频率，选取了两组不同频率、相同幅值的水流荷载分别对混凝土拱坝整体结构以及成层结构进行有限元数值计算。其中荷载一主频带约在0.5～3.0 Hz之间（以下简称高频荷载），荷载二主频带约在0～0.5 Hz之间（以下简称低频荷载），其频谱特性见图6。
3.1 结构自身特性与振动响应之间的关系
为了准确分析结构自身特性与振动响应之间关系，在坝体模型上共布置19个测点以提取结构的动应力及动位移响应数据，测点分布见图7。共进行了4种工况（见表3）的计算，每种工况计算2 000步。
荷载二作用下，整体结构坝顶拱圈测点的动位移均方差明显小于成层结构，最大差值约为103 μm，约占整体结构均方差的19.4%。而在荷载一作用下，整体结构与成层结构坝顶拱圈测点动位移均方差大致相当，两条曲线基本重合。
如图9-图10所示，坝体拱冠梁处测点动应力均方差呈反“S”型分布，在坝高160 m处均方差达最大值。在荷载二作用下，拱坝整体结构在拱冠梁处测点动应力均方差略小于成层结构，在坝高160 m处均方差差值最大，差值约为3.0 kPa，占整体结构均方差的33.4%。而在荷载一作用下，拱坝整体结构与成层结构在拱冠梁测点处动应力均方差大致相当，两条曲线时有交叉，最大差值也出现在坝高160 m处，约为1.5 kPa，占整体结构均方差的9.0%。
拱冠梁处动位移均方差则表现为自下而上逐渐增大的趋势。在荷载二作用下，整体和成层结构拱冠梁处均方差均随着坝体的升高而增大，同时两种结构均方差的差值也增大。成层结构位移均方差始终大于整体结构，最大差值出现在坝顶位置，约为103 μm，占整体结构均方差的19.4%。在荷载一作用下，两种结构拱冠梁处动位移均方差的变化趋势相同，而均方差差值却是先增大后减小，最后在坝顶位置基本趋于一致。但两种结构位移均方差的差值并不大，最大差值出现在坝高160 m处，差值约为26 μm，占整体结构均方差的7.4%。
由此可见，拱坝成层结构动位移及动应力均方差均大于混凝土整体结构，而高频荷载作用下成层结构响应不及整体结构灵敏。
3.2 泄流荷载与振动响应之间的关系
本文主要研究不同频谱特性泄流荷载与结构振动响应之间的关系。如图8所示，结构在荷载一作用下动位移均方差明显大于荷载二，最大值出现在拱冠梁顶端。整体结构均方差的最大差值为191 μm，约占荷载二作用下动位移均方差的35.9%；成层结构为105 μm，约占荷载二作用下动位移均方差的16.5%。
又分别见图9-图10，高频荷载作用下结构动应力均方差明显大于低频荷载作用，在坝高160 m处测点动应力均方差出现最大值。整体结构均方差的最大差值为8.58 KPa，约占低频荷载作用下动位移均方差的98.4%，均方差增大了近一倍；而成层结构最大差值为7.21 KPa，约占低频荷载作用下动位移均方差的61.9%，均方差也增大了0.6倍左右。在拱冠梁处结构的动位移均方差也均有所增加，在拱冠梁顶端达到最大，整体结构增大了35.9%，成层结构增大了16.6%。
综合以上分析结果可知，同一结构在相同幅值、不同频谱特性的荷载作用下，振动特性存在如此大的差距，很有可能是结构在高频荷载激励下产生了水力共振现象。
4 泄流荷载作用下成层结构振动特性
在坝顶拱圈自右岸至左岸依次布置B1至B7共7个测点，拱冠梁方向自上而下依次布置B8至B12共5个测点，测点布置见图7。
4.1 拱坝坝顶拱圈测点的振动现象
工况2 条件下，结构仅在2.1Hz处存在一明显峰值，根据拍振的形成机理，该测点不具备形成拍振的条件，在时程曲线上表现为随机振动的形式，振动曲线并未出现“拍”现象。
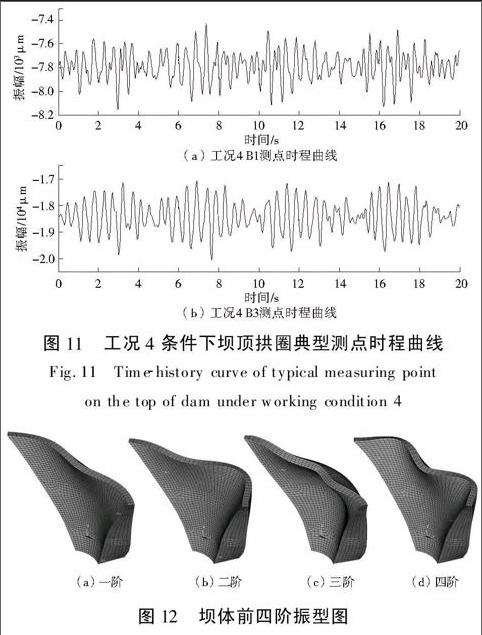
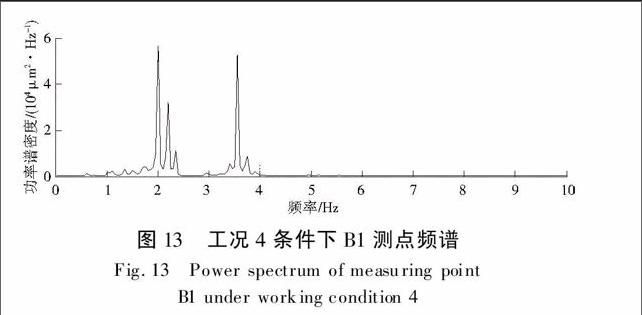
图11为工况4条件下坝顶拱圈典型测点时程曲线，从图中可知B3测点表现出较为明显的“拍”现象；而拱圈上B1测点靠近坝肩，受力条件复杂，由于测点基本位于各阶振型的节点处，振动量较小（图12）。如图13，B1测点以拱坝的前四阶工作频率振动；由模态识别结果知，前四阶频率分别为2.20 Hz、2.35 Hz、3.56 Hz和3.72 Hz，频率比不符合式（7）给出的拍振形成条件，故此节点并未表现出较为明显的“拍”现象。
4.2 拱坝拱冠梁测点的振动现象
拱坝拱冠梁处由上而下依次布置B4及B8至B12共6个测点，其典型测点时程曲线见图15。可以看出B4、B8测点表现出较为明显的“拍”现象，其余测点则随着位置距坝顶距离的增大，“拍”现象愈加不明显， B12测点振动曲线则完全看不出“拍”现象的存在。
B4测点主要以拱坝的第一阶固有频率振动，并包含微弱的第三阶振动成分（图16）。其振动曲线虽然表现为“拍”的形式，但其振动的实质是水流荷载激励下其瞬时频率与结构一阶固有频率接近或重合时所发生的“水力共振”现象[5]。
B8测点虽处于拱冠梁位置处，但并未处于其顶端，从频谱图也可以看出B8测点以结构前两阶固有频率振动，频率比符合式（7）所提出的拍振形成条件，其振动体现为明显的拍振现象。
B9测点以下各测点处振动量逐渐减小，约束条件愈加复杂。如B10测点振动不能满足式（7）提出的拍振形成条件，振动曲线看不出“拍”现象（图17）。
5 结论
本文研究了整体与成层两种不同结构在泄流荷载作用下结构的响应特性，又结合“拍”的概念，对混凝土成层结构振动响应特性与泄流荷载之间的关系进行分析，得出以下结论。
（1）在泄流荷载作用下，混凝土成层结构的振动响应大于混凝土整体结构；成层结构在荷载一、二分别作用下，振动响应变化量不及整体结构，表明不同结构在不同泄流荷载作用下反应的灵敏度不同，成层结构对不同频谱特性的荷载反应不及整体结构灵敏。
（2）在泄流荷载作用下结构主振型方向，当结构前n阶频率f1至fn位于荷载主频带范围内时，荷载将激发结构前n阶频率产生共振，流激振动响应可能存在以下几种形式：①当n=0时，结构无低阶频率处于水流荷载主频带以内，结构在泄流荷载作用下做随机振动，振动能同时体现出荷载特性及结构第一阶的振动特性，但并未产生共振；②当n=1时，结构只有一个低阶频率位于泄流荷载的主频带以内，在荷载作用下以该低阶频率做随机共振，响应不满足拍振的形成条件，但体现为水力拍振的形式，其功率谱曲线会在该频率处存在明显的峰值；③当n≥2时，结构存在两个或以上低阶频率位于泄流荷载的主频带内，若f1至fn两两之间的频率比满足0.85≤α≤1.18的要求，结构各阶自振响应将互相叠加，形成拍振，其响应也体现为水力拍振现象；若不满足，结构各阶自振响应叠加后不会形成拍振，其响应体现为不明显或不出现水力拍振现象。
（3）无论是水力共振或是拍振，均会加剧结构的振动，在泄流荷载的长期作用下，可能使结构出现疲劳破坏。在现实工程中应调整泄流方式，避免水力共振或拍振的发生。[HJ1.65mm]
参考文献（References）：
[1] 练继建，马斌，李福田.高坝流激振动响应的反分析方法[J].水利学报，2007，38（5）：575-581.（LIAN Ji- jian，MA Bin，LI Fu-tian.Back analysis algorithm for response of flow-induced vibration in overflow high dam[J].Journal of Hydraulic Engineering，2007，38（5）：575-581.（in Chinese））
[2] 杨敏，崔广涛.水工结构流激振动的综合集成探讨[J].水力发电学报，2008，27（1）：102-110.（YANG Min，CUI Guang-tao.Synthetic discussion on flow-induced vibration of hydraulic structures[J].Journal of Hydroelectric Engineering，2008，27（1）：102-110.（in Chinese））
[3] 阎诗武，骆少泽，陈发展.飞来峡溢流坝结构流激振动[J].水利水运科学研究，1997（3）：228-236.（YAN Shi-wu，LUO Shao-ze，CHEN Fa-zhan.Flow-induced vibration of feilaixia spillway dam structure[J].Hdro-science and Engineering，1997（3）：228-236.（in Chinese））
[4] 沈崇刚.中国碾压混凝土坝的发展成就与前景（上）[J].贵州水力发电，2002，16（2）：1-7.（SHEN Chong-gang.Achievement & Prospects of rolled compaction concrete dam in China（first half）[J].Guizhou Water Power.2002，16（2）：1-7.（in Chinese））
[5] Naudascher E.Flow-induced loading and vibration of gates in proc int symp on hydr for high dams [C].Beijing，Invited Lecture，1988：1-18.
[6] 李成业.泄流结构水力拍振机理及动态健康监测技术研究[D].天津大学，2013.（LI Cheng-ye.Research on hydraulic beat mechanism and dynamic health monitoring method of flood discharge structures[D].Tianjin University，2013.（in Chinese））
[7] 韩军，高德平，胡绚，等.韩军航空发动机双转子系统的拍振分析[J].航空学报，2007，28（6）：1370-1373.（HAN Jun，GAO De-ping，HU Xuan，et al.Research on beat vibration of dual-rotor for aero-engine[J].Acta Aeronautica Et Astronautica Sinica，2007，28（6）：1370-1373.（in Chinese））
[8] 应怀樵.波形和频谱分析与随机数据处理[M].北京：中国铁道出版社，2003.（YING Huai-jiao.Analysis of waveform and spectrum and rand-om data processing [M].Beijing：China Railway Publishing House，2003.（in Chinese））
[9] 苏未安，陈秀洪.用旋转矢量法研究“拍”现象[J].江西理工大学学报，2009，30（1）：60-63.（SU Wei-an，CHEN Xiu-hong.Study on “beat” phenomenon with the method of rotating vector[J].Journal of Jiangxi University of Sience and Technology，2009，30（1）：60-63.（in Chinese））
[10] 王永涛，臧勇，吴迪平等.CSP轧机扭振中“伪拍振”的研究[J].振动、测试与诊断，2009，29（2）：210-213.（WANG Yong-tao，ZANG Yong，WU Di-ping，etal.Fake beating vibration in main driving torsion of CSP mill[J].Journal of Vibration，Measurement & Diagnosis，2009，29（2）：210-213.（in Chinese））
[11] 周康巍.拍现象与外差变频的区别[J].大学物理，1983，（5）：1-4.（ZHOU Kang-wei.The difference between the beat phenomenon and heterodyne frequency [J].DaXue WuLi，1983，（5）：1-4.（in Chinese））
[12] 练继建，李成业，刘昉，等.环境激励下二滩拱坝拍振机理研究[J].振动与冲击，2012，31（3）：1-7.（LIAN Ji-jian，LI Cheng-ye，LIU Fang，et al.Beat vibration of earth arch dam under ambient excitation[J].Journal of Vibration and Shock，2012，31（3）：1-7.（in Chinese））
[13] 练继建，崔广涛，黄锦林.导墙结构的流激振动研究[J].水利学报，1998，（11）：33-37.（LIAN Ji-jian，CUI Guang-tao，HUANG Jin-lin.Study on flow induced vibration of spillway guide wall[J].Journal of Hydraulic Engineering，1998，（11）：33-37.（in Chinese））
[14] 徐国宾，尹伟波，练继建，等.糯扎渡水电站溢洪道泄槽流激振动试验研究[J].水利水电科技进展，2007，27（6）：24-27.（XU Guo-bin，YIN Wei-bo，LIAN Ji-jian，etal.Experimental study on flow-induced vibration in spillway chute of Nuozhadu hydropower station[J].Advances in Science and Technology of Water Resources，2007，27（6）：24-27.（in Chinese））
[15] 崔广涛，安刚，李军.低水头大流量溢流坝系统水激振动研究[J].水利学报，1994，（1）：10-18.（CUI Guang-tao，An Gang，LI jun.Flow-induced vibration of low head and large discharge over flow dam[J].Journal of Hydraulic Engineering，1994，（1）：10-18.（in Chinese））
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2024/12/22 20:57:45