《土石坝渗漏的启发式反算分析》-工学论文，工程论文-论文范文参考-科学狗论文网

标题

土石坝渗漏的启发式反算分析

范文

赵冲

摘要：本研究以土石坝的渗流问题为例，利用启发式优化反演计算分析、监测数据使用、数值模拟分析，找出监测数据异常的原因，找出大坝异常诊断和解释的方法。

Abstract： This study takes the seepage problem of earth-rock dam as an example， uses heuristic optimization inversion calculation analysis， monitoring data usage， numerical simulation analysis， finds out the causes of monitoring data anomalies， and gives the methods for dam abnormal diagnosis and interpretation.

关键词：土石坝;渗流;启发式优化算法;和弦搜寻算法

Key words： earth-rock dam;seepage;heuristic optimization algorithm;chord search algorithm

中图分类号：TV641 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文献标识码：A ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文章编号：1006-4311（2019）13-0128-03

1 ?研究动机

土石坝不可能完全无渗漏，但如果渗漏过多，将导致蓄水能力下降。更严重的是反常的渗漏进入大坝，水力梯度过大，可能导致大坝内部侵蚀，逐渐扩大形成管道，最终导致大坝完全破坏。如果监测数据异常，应通过诊断大坝内部问题来找出异常原因，但如何诊断大坝可能出现的问题是非常困难的。本研究的目的是通过优化反算分析，以土石坝渗流问题为例，利用监测数据和数值模拟分析，找出异常监测资料产生的原因，找出异常坝体的诊断和解释方法。

2 ?研究方法

本研究选择MATLAB为主控程序，执行优化算法，结合FLAC v4.0有限差分软件进行渗流分析模拟，选用和弦搜寻算法作为本研究工程优化求解法。

和弦搜寻优化演算流程：问题数学化→定义各参数值→产生1组初始和弦记忆（HM）→一次迭代产生1个新的和弦（H）→是否更新HM→重复步骤4和步骤5，直到达终止目标为止。

3 ?优化搜寻模式验证

3.1 土石坝A案例验证结果

A坝体材料渗透系数设定值中，中心层水平透水系数与壳层透水系數均设为待定变数，并且■=4。考虑目标因子为总坝体渗流量（Q），其目标设计值为 88.93CMD。

和弦记忆（HM）迭代次数和目标函数均值曲线表明，已经进行了130次搜索，HM函数均值收敛到0.0000479。在HM渗流平均迭代次数（n）和目标因子图中，60次HM搜索的平均值接近88.93 CMD的目标值。

此外，从2个待定变数的HM平均值与迭代搜寻次数关系图显示，心层水平透水系数经优化搜寻过程渐渐趋近真实值4×10-7cm/sec;壳层透水系数向真实值5×10-5cm/sec收敛。

优化搜寻中，最佳目标值和弦的饱和度迭代次数（N）=109;目标函数值=0.0000055;坝体总渗流量=88.72CMD;心层的kh=2.53×10-7cm/sec;壳层的k=5.89×10-5cm/sec。A坝案例的真实值与最佳HM130（依目标函数值从小到大排序）的目标函数值（f_obj）、总渗流量（Q）与心层水平透水系数（kh_core）和壳层透水系数（k_shell）两待定变数值进行比较，另由最佳10个和弦平均值各项结果显示，均与真实值相近，因此可看出待定变数值最佳解并未发生陷入局部解情形。

3.2 土石坝B案例验证结果

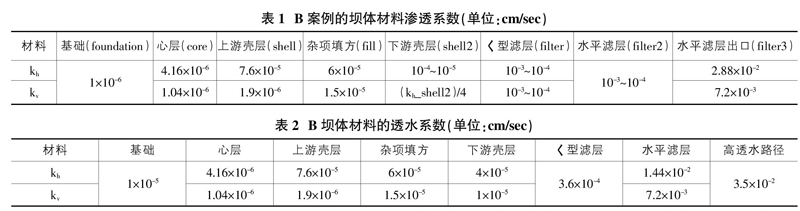
表1为B坝体材料渗透系数，其中kh_shell2、kv_shell2、kh_filter、kv_filter、k_filter2均设定为变数，满足kh？叟kv与■=4。目标因子：总坝体渗流量与两个水位观测井总水头。

弦记忆目标函数的迭代次数（n）与平均值（HM）之间的关系表明，搜索总数为350，最终的HM函数的平均值收敛到0.000103左右。根据渗透系数平均值与HM迭代次数的关系，可以看出，180次搜索后HM的平均值约为目标值119.18CMD。在另外两个HM中，总水头系数（Th1和Th2）与迭代次数相关，Th1的207次搜索后，HM的平均值约为41.22m，Th2的141次搜索后，HM的平均值约为38.95m。由此可见，Th1的收敛速度最慢，因此目标函数的207次搜索函数的平均值为0.000152，接近最终收敛平均值。

将4个待定变数的HM平均值与迭代搜寻次数的搜寻结果显示：

①下游壳层水平透水系数平均值渐渐趋近6×10-5

cm/sec（真实值=4×10-5cm/sec）;

②く型滤层水平透水系数平均值渐渐趋近4×10-4

cm/sec（真实值=3.6×10-4cm/sec）;

③く型滤层垂直透水系数平均值渐渐趋近2.2×10-4

cm/sec（真实值=3.6×10-4cm/sec）;

④水平滤层透水系数平均值渐渐趋近3.6×10-4cm/sec（真实值=3.6×10-4cm/sec）。

在350次迭代中，计算出最优目标函数值，即第101次迭代（（N_saerch=101）和目标函数值（fmin._obj）为0.0000597。坝体渗透量（HM_Q）为120.04Cmd，接近119.18CMD的目标值。总水头目标值为Th1，即41.33m，非常接近41.22m的目标值，水头目标系数Th2为38.95m，相当于38.95m的目标值。在四个未定变量中，水平滤层的渗透系数最接近实际值。

B案例的待定变数值与最佳HM350（依目标函数值从小到大排序）的目标函数值（f_obj）、总渗流量（Q）、总水头（Th1、Th2）与下游壳层水平透水系数（kh_shell2）、く型滤层水平与垂直透水系数（kh_filter、kv_filter）、水平滤层透水系数（k_filter2）四个待定变数值比较结果显示，10个最佳和弦的k_filter2与真实值最为接近，而其他三个待定变数值与原设计值也在同一乘幂（order），其差值约在一个调整幅度范围（bw=2单位）内，四个待定变数值对于目标函数影响敏感性大小排序为：k_filter2>kh_filter>kv_filter>kh_shell2。

综合以上结果显示，本研究使用和弦搜寻（HS）最佳化演算法，使用简单原理及一些基本数学技术的条件，就能够将HS演算法在函数值搜寻速度与收敛性能的优点充分表现出来。

4 ?和弦搜寻法反算-土石坝B案例

分别以两个不同假设情境进行和弦搜寻优化算法的反算分析，探讨可能的透水路径，以符合观察的下游坝面渗漏点位置与下游壳层的水头测量。

情境 1：

假设B坝体下游壳层内存在一高透水路径，此高透水路径的透水系数为已知，且路径厚度均固定在2m，路径的几何路线以二次函数表示为变数形式。下游坝面渗漏点位置与渗漏出水量已知。

情境 2：

假设B坝体下游壳层内存在一高透水路径，此高透水路径的透水系数为已知，路径的几何路线以二次函数表示为变数形式，且设定其厚度范围为{2，4，6，8，10} m的离散变数，其中路径厚度不随x方向的增减而变化。除了下游坝面渗漏点位置与渗漏出水量已知，下游壳层内有三处的水头测量值也已知。

以上两种情境的优化反算分析中，均藉由比较FLAC分析结果与已知观测数据，由各项差值正规化后的平方和来计算目标函数值。表2为B坝体中各部分材料所假设的透水系数。

4.1 情境1反算分析结果

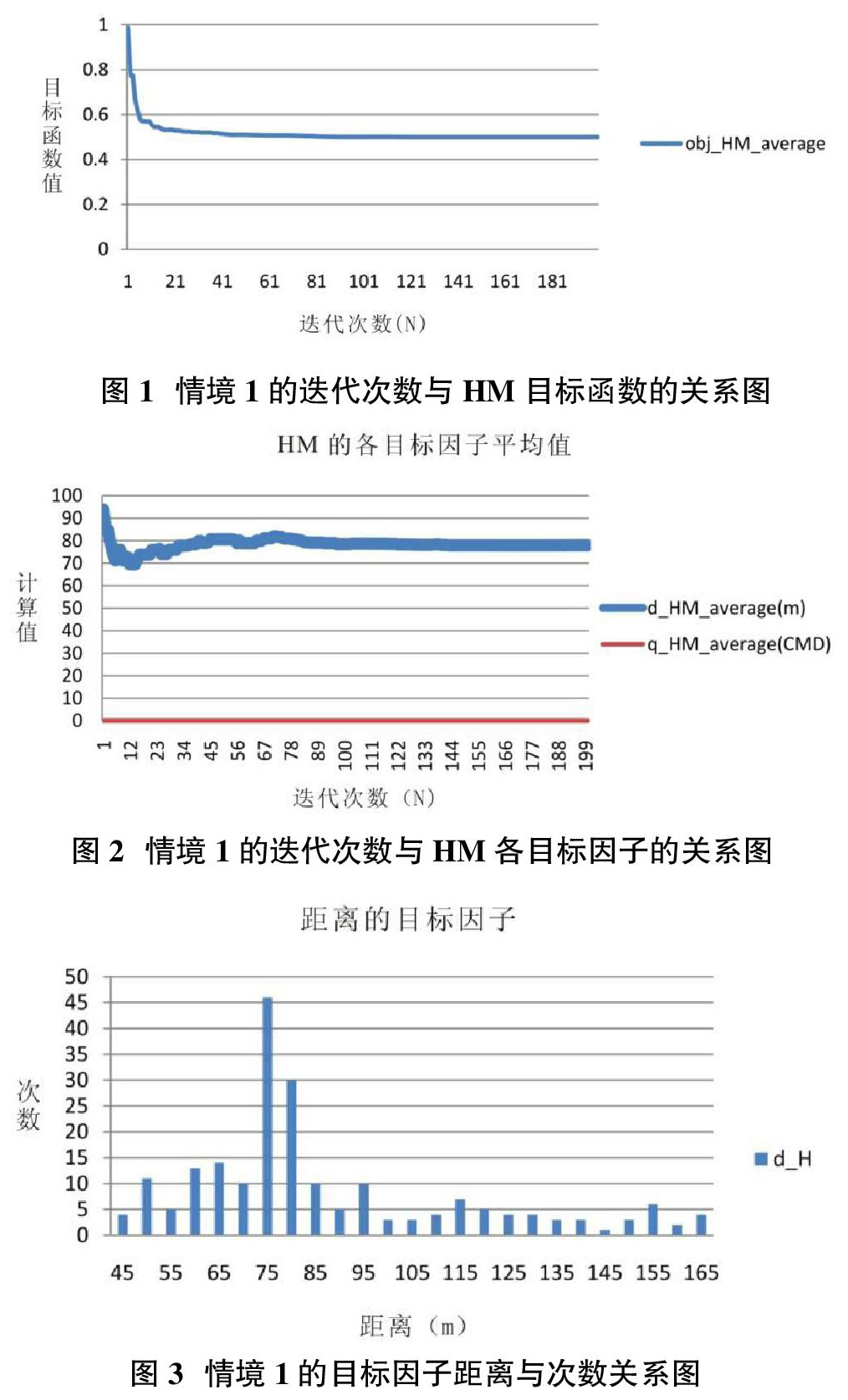
图1为迭代次数与和弦记忆（HM）的平均目标函数值的关系图，共搜寻了200次，最后HM的目标函数平均值约收敛至0.50004。图2为迭代次数与HM的各目标因子平均值的关系图，其中距离目标因子搜寻32次之后的HM平均值，均在目标观测值77.91 m上下;渗流量目标因子计算值均为0CMD。图3为每次迭代产生的目标距离值与其次数的统计资料，记录最多次数的距离为75m至80m，共出现46次。

和弦记忆大小为10 （HMS=10）的初始和弦记忆（HM0），其中HM0的10个和弦（H）系按随机产生的顺序排序。以5_HM0为例，代表10个初始和弦记忆中的第五个随机产生的和弦。

迭代200次（N=200）之后的和弦记忆（HM200），按目标函数值（f_obj）由大至小顺序排列的材料分区图与其右上角为对应的饱和度图结果显示，标示于图左上方的f_obj 为当次迭代所产生的目标函数值，函数值越小表示与目标观测值越接近。

4.2 情境2反算分析结果

迭代次数与和弦记忆（HM）的平均目标函数值关系图显示，共搜寻115次，最后HM函数平均值约收敛至0.50366。迭代次数与HM中的各目标因子平均值关系图显示，其中距离目标因子搜寻第40次之后的HM平均值，均在目标观测值77.91m上下;渗流量目标因子计算值均为0CMD;另外三个水位观测井计算的孔隙水压值均为 0，也就是总水头等于位置高程。

和弦记忆大小为10 （HMS=10）的初始和弦記忆（HM0），其中HM0的10个和弦（H）系按随机产生的顺序排序。迭代115次（N=115）之后的和弦记忆（HM115），依目标函数值（f_obj）由大至小顺序排列的材料分区图与其右上角为对应的饱和度图，其表示以图4为例，其中标示于图左上方的f_obj 为当次迭代所产生的目标函数值，函数值越小表示与目标观测值越接近。值得注意的是，在这十种情形下，下游侧的浸润线皆位于水平滤层，完全没有进入下游壳层之内。

4.3 小结

本研究拟定的两种情境主要是依据B坝实际案例进行模拟，希望能通过优化算法的反算分析，来模拟坝体Sta.0+170m的横断面所观察到下游壳层的下游边坡平台处附近出现渗漏水现象的可能原因，因此假设下游壳层存在一高透水路径。其中情境2额外考虑下游壳层水位观测井的水位（水头）资料，并假设高透水路径可能为下游壳层内的一条高透水带，允许路径厚度范围为{2，4，6，8，10} m之一的离散变数形式。

由4.1节与4.2节的两情境反算分析结果显示：①目标函数收敛性良好;②情境1最佳目标函数值为0.500001，情境2最佳目标函数值为0.503567，两者目标函数值0.5的数值即为渗流量目标因子的权重（？琢q=0.5），而情境2目标函数值0.003565的数值则为三个水位观测井计算产生的数值。③由于情境2额外限制高透水路径，必须在三个水位观测井间的水位以上，因此情境2迭代次数（N=115）明显比方案1 （N=200）少。

5 ?结论

①本研究使用优化算法，以分析软件FLAC进行计算分析，得出的两个验证案例结果显示，以坝体总渗流量或加上水头作为目标观测因子，能有效反映坝材透水系数求解，并且与真实值相近。

②假设部分坝材透水系数为待定变数，经迭代过程，均能有效快速收敛至与原设计值相近的范围内，不过随着迭代次数增加，函数解每次更新，所需的搜寻次数相对增加，以致越后期越需耗费更多搜寻时间才能更接近目标值。而B验证案例的待定变数数量是A验证案例的两倍，其计算量增加仅约为2.7倍，由此可看出对于变数值的多种组合问题所需求解时间，不会因变数量增加使得搜寻迭代次数呈指数上升趋势。

③一般限制条件越多表示问题特性相对较复杂，不过与变数相关的边界限制条件越多，将会缩小搜寻范围，使得进行目标函数计算之前能先剔除不符合条件，避免耗费太多不必要的计算时间或资源。由B坝案例两种情境反算结果显示，目标函数值虽能有效收敛，但并非收敛至函数值为零的目标，而是收敛至某特定值，且主要随距离因子做函数值收敛，分析当有某些观测因子对于此问题型态的求解，无法展现其作用亦或是定义优化问题的和学模式化时，问题本身就存在缺陷或是没充分将问题性质以公式表达出来。

④本研究反算结果推论，应可排除库水经下游壳层的高透水通道造成下游坝面平台处渗出水，且应与浸润面并无关联。分析坝面平台处渗出水较可能为下游壳层中因为材料透水性不均匀，下雨入渗后留在低透水性壳层材料的栖止水，慢慢迂回经过较为透水的通路流出所致。

参考文献：

[1]杨青.土石坝渗流分析在阿勒腾也木勒水库排除沥青心墙渗漏的应用[J].西部探矿工程，2014，26（7）.

[2]刘川顺，韩东平.土石坝渗漏原因的相关分析法[J].中国农村水利水电，2003（6）.

[3]陈建强.大中型水库土石坝工程渗漏问题及处理方法分析[J].农业科技与信息，2016（12）.

[4]付仕余，梁经纬.湖南省小型水库土石坝涵管渗漏原因及处理方法调查研究[J].湖南水利水电，2016（6）.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。