网站首页  词典首页

请输入您要查询的论文：

　

标题 HPM视角下的数学教学设计
范文



[摘 要] 初中数学教师应用HPM教学方法引导学生学习，实则是为了让学生深入地理解某一个重要的数学知识以后，能够让学生由这个数学知识为核心，自主地学习与之相关的其他数学知识.本次研究将以勾股定理为例，说明HPM视角下初中数学教学设计的方法.
[关键词] 数学史；勾股定理；教学设计HPM即History and Pedagogy of Mathematics，用HPM视角引导学生学习数学，即将数学史引进到教学当中，让学生以历史的角度看待一个数学问题的提出、数学问题的演变、数学问题的应用等. 数学教师如果应用这种方法引导学生学习知识，学生将能深入地理解到探索数学知识的重要意义、人们拓展数学知识系统的整个过程、人们逐步完善数学知识系统的方法. 如果教师能够引导学生以HPM的视角纵向了解某个数学知识，学生将会以该数学知识为中心，形成一套完善的数学知识系统. 本次研究将会以初中数学勾股定理的教学设计来说明HPM视角在数学教学中的应用方法.
结合历史，让学生探究勾股定理的概念
勾股定理，是一个直角三角形的平方和等于斜边平方的数学定理. 从几何的角度来说，它是几何知识的一个重要基础，从函数的角度来看，它是余弦定理的一个特例. 数学教师如果能在勾股定理这一章节为学生打下良好的数学基础，学生就能够打好学习几何知识与函数知识的基础.
如果数学教师仅仅让学生单纯地理解勾股定理这一概念，学生将只能理解“勾三股四弦五”这一条文字概念，教师要学生真正地理解这一条数学概念背后隐藏着各种数学知识，就需要让学生从数学史的角度去了解勾股定理的知识. HPM视角下的数学教学实际上就是让学生从宏观的角度去了解古人是如何摸索出这一条定理、研究这一条定理、应用这一条定理的.
以一名教师引导学生深入的理解勾股定理为例，教师可让学生看到欧几里德、郑爽等人的定理证明方法，然后引导学生思考，为什么前人已经证明过这条数学定理以后，后人还要继续探索新的求证方法呢？学生经过思考能够理解到，在学习数学的过程中不能盲从前人说过的话，而要自己探索、自己思考，直到探索出数学知识的奥秘. 这时教师可引导学生用一套全新的方法证明勾股定理. 有一名学生的证明方法如下：
参看图1，在直角△ABC斜边上绘制正方形ABDE，延长CB，从E点作CB延长线的垂直线EG，两线的焦点为G. 从D绘制CB的垂直线，它相交于CB延长线的K点. 以A点绘制EG的垂直线，它的交点为F. 以D点绘制EG的垂直线，它的交点为.
从图1绘制的过程可看到△AFE≌△EHD≌△BKD≌△ACB.
如果将五边形ACKDE的面积视为S，可得S=SABED+2S△ABC；（公式1）
同时可得S=SACGF+SHGKD+2S△ABC；（公式2）
由公式1、公式2可得c2+2×ab=b2+a2+2×ab；
由此可得c2=a2+b2.
教师引导学生从HPM的视角看待数学知识，并不是单纯地为了让学生了解数学的历史，而是要让学生从历史的角度了解到前人不懈的探索数学知识的精神、古人追寻数学真理的态度. 当学生了解到这一点后，学生就能了解到自己学习数学知识的目的不是为了记住一个数学概念、数学定理，而是要用自己的头脑去思考数学的问题、用自己的实践去验证数学的知识、用自己的视角去开辟数学的新天地.
数学教师应用HPM视角引导学生学习时，不能仅仅着眼于让学生去学习数学历史，而要从引导学生了解数学概念产生、演变、应用出发，让学生从中理解到追寻科学、追寻真理的精神，学生只有拥有这种科学探索的精神，才能学好数学知识.
巧设习题，让学生感受勾股定理的变化
如果以HPM的视角来看，人们全面地了解一个数学知识需要漫长的时间，在探索数学知识的过程中，人们发现了一个数学概念就会去积极探究这个数学知识，然后人们会逐渐完善数学知识、拓展数学知识. 以勾股定理为例，“勾三股四弦五”只是勾股定理的基本描述，以后人们在了解这条定理的基础上发现了“两条边的平方和等于斜边的平方和”这一个规律. 教师如果在教学的时候能让学生去探索勾股定理拓展的过程，学生将能领略到数学知识变化的奥妙，他们的学习兴趣会被激发，他们在探索的过程中会初步地形成一个数学知识系统.
以教师引导学生看两个习题为例：
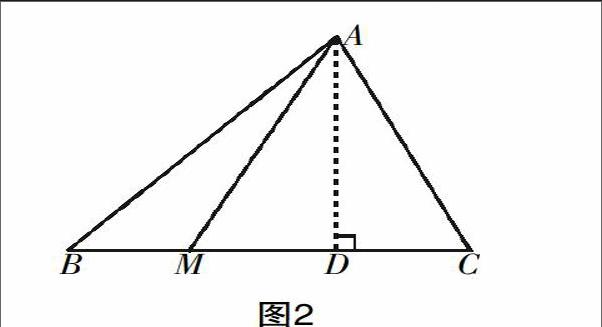
习题1：参看图2，AM是△ABC中BC边的中线，求证：AB2+AC2=2（AM2+BM2）.
[A][B][C][D][M]
一名学生的求证方法如下：
从A点绘制BC边的垂直线，交点为D，由c2=a2+b2可得AB2=AM2+BM2+2BM·MD；（公式3）
由此可推知，在△ACM中，AC2=AM2+MC2+2MC·MD；（公式4）
AM是△ABC中BC边的中线，可得MB=MC；
由公式3与公式4可得AB2+AC2=2（AM2+BM2）.
学生从这个证明的过程中能推知三角形的中线长公式，他认为假设△ABC的边长分别为a，b，c，它们对应的中线长为ma，mb，mc，那么中线长的公式为：
ma=，
mb=，
mc=.
当学生能够从勾股定理推知三角形的中线长规律时，学生就能感受到数学知识蕴藏很多变化.
此时教师可引导学生再做习题2：
求证：四边形四条边的平方和为对角线的平方和与对角线中连线平方之4倍.
由于学生有习题1作为基础，他们可以较为轻松地找到求证的方法，这名学生的求证过程如下：
参看图3，四边形ABCD的对角线分别为AC，BD，由三角形中线长的定律，可得BQ2+DQ2=2PQ2+2·2
2=2PQ2+；
将之简化可得2BQ2+2DQ2=4PQ2+BD2；（公式5）
[A][B][C][D][O][P][Q]
图3
结合习题1中证明的三角形中线长公式，可得
BQ2=（2AB2+2BC2-AC2）；（公式6）
DQ2=（2AD2+2DC2-AC2）；（公式7）
将公式6和公式7代入公式5中，可得（2AB2+2BC2-AC2）+（2AD2+2DC2-AC2）=4PQ2+BD2，于是AB2+BC2+CD2+DA2=AC2+BD2+4PQ2.
学生在做习题2的时候，能从三角形中线长公式中研究出一种新变化.
从教师引导学生从勾股定理开始，教师可让学生探索三角形中线长的公式，再引导学生灵活应用三角形中线长的公式，在这个学习过程里学生能了解到数学知识的变化、感受到数学知识的乐趣. 当学生能够从勾股定理中拓展出新的数学知识时，他们将能感受到数学知识系统形成的脉络.
数学教师应用HPM的方式引导学生学习数学的时候，可以从数学史的角度给学生布置习题，学生在体验数学知识演变的过程中能初步形成数学知识系统，这是他们完善数学知识系统的基础.
结合实践，让学生理解勾股定理的系统
当教师从HPM的角度引导学生感受到数学知识系统的脉络以后，教师可引导学生尝识系统地总结数学知识，学生在总结数学知识以后，将能从HPM的角度看到数学知识系统的形成，这个数学知识系统将成为学生深入地学习与之相关数学知识的基础.
以教师引导学生学习勾股定理为例，教师在让学生以HPM的角度纵向地了解到勾股定理以后，引导学生系统地总结勾股定理的描述，有一名学生的描述如表1：
表1为学生总结的勾股定理的知识系统，学生完整地总结出这个知识系统以后，就可以应用这套知识解决与之相关的数学知识，从而拓展出新的数学系统.
以学生学习勾股定理为例子，教师以HPM视角引导学生学习数学知识，学生就能够以该知识为基础，学习与之相关的其他数学知识，比如学生可以进一步探索勾股定理的逆定理、直角三角性的性质以及判定、直角三角形的边与角之间的关系等几个方面的知识，从而学生的数学知识系统将能层次分明、联系紧密，学生如果能熟知数学知识与数学知识之间的内在联系，他们以后就可灵活地应用这些知识解决数学问题.
本次研究以勾股定理的教学案例为参考，说明了HPM视角的教学设计方法.初中数学教师应用HPM视角引导学生学习时，要引导学生深入地理解数学知识、引导学生探索数学知识的变化、引导学生系统地学习数学知识.初中数学教师应用这种教学方法引导学生学习，实则是为了让学生深入地理解某一个重要的数学知识以后，能够让学生由这个数学知识为核心自主地学习与之相关的其他数学知识，在这个过程中，教师能够培养出学生探索科学知识的精神、激发学生学习数学的习趣、提高学生认识事物的能力.
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2024/12/22 16:00:28