网站首页  词典首页

标题	从“错误”中生成教学资源策略例析
范文	高建芳 [摘 要] 数学错误借助适当的策略可以生成教学资源. 数学教师不妨营造适宜的教学情境，引领学生寻找、交流、评价错误，发挥教师的主导作用和学生的主体地位，从而将数学错误转化为数学价值. [关键词] 数学错误；教学资源；生成；寻找；评价 由于学生认知结构失衡和心理状态的复杂性等多种因素，学生的作业出错总是不可避免. 作为教师，如果能够正确处理数学作业“错误”，将对提高学生的数学能力起着举足轻重的作用. 梳理各种错误类型，我们不难发现，这些错误包含理解和运用数学知识的诸多问题：（1）思维误区；（2）心理障碍；（3）熟练程度不够；（4）综合性分析能力欠缺；（5）作业设置超出学生的认知水平等. 可见，排除了这些错误，就意味着学生能够进入“山重水复疑无路，柳暗花明又一村”的境界，能够极大地提高数学成绩. 因此，这些资源极有教学价值. 心理学家盖耶认为：“谁不考虑尝试错误，不允许学生犯错误，就将错过最富成效的学习时刻. 我们要善待学生的‘错误，抓住这种数学教育契机，让错误变成宝贵的教学资源. ”那如何生成呢？ 寻找策略 寻找策略指有组织、有目的地搜寻错误的方式、方法. 运用这种策略可以帮助师生有趣味、有效率地快速发现数学错误，生成教学资源. 一般而言，数学作业的批改主体过于单一，绝大多数是由教师承担的. 这当然可以让教师最快速地了解学生的学习状态，却不能深层次地锻炼学生，不能驱动他们的自主性. 因此，除了重大的考试、检测外，我们完全可以放手让学生分组批改，然后梳理、归纳错误. 在学生批改的过程中，一方面能检测批改者的学习状态，另一方面，能帮助被批改者寻找错误. 学生经历了这样的批改体验，就等于自行构建了一个交流的公共平台，会使他们忌讳再次出现类似的错误，也会极力避免简单、低级错误的产生，从而悄无声息地帮助他们建立一个良好的监督机制，约束他们尽可能地减少错误. 当然，教师的主导参与作用也不可省去，可以通过巡视、抽查、交流等形式帮助学生发现、归类错误. 评价策略 评价策略指针对数学错误而展开的反馈、评价和修正等一系列行动的方式、方法. 数学作业设置的目的“不仅应当是程序性知识的简单再现式巩固，更应体现对‘教与‘学的诊断作用，体现在对学生认知结构‘顺应的催化上”. 学生作业错误率在面积和题型上均呈现高比率，这说明教学改进的空间十分巨大，且必须及时采取有效的应对策略. 1. 对话交流 组织有效的对话交流平台，能够利用集体的智慧发现错误的原因，寻找避免错误的方法，从而修正错误，获得正确的认知. 这在多层次和多元指向性的作业中尤其具有极强的有效性. 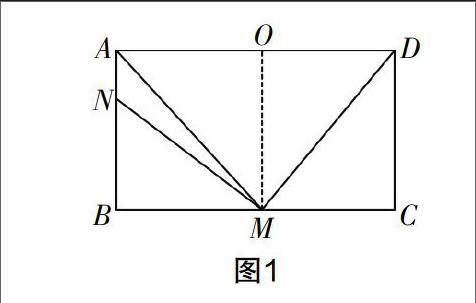案例1？摇 如图1所示，在矩形ABCD中，M，N分别是边BC，AB上的点，且MN=MD，MN⊥MD，求证：AM平分∠BAD. 错误？摇 过点M作AD的垂线段MO，可得四边形ABMO为矩形. 因为AM为其一条对角线，由MB⊥AB，MO⊥AD可知，MO=MB，所以AM平分∠BAO，也即平分∠BAD. 师：同学们看看，王亮（化名）这道题证明得正确吗？ 生1：不正确. 已知条件怎么没有充分利用上去啊？ 生2：不对，四边形ABMO为矩形，这一点没错. 但是请问王亮，你怎么知道AM就一定平分∠BAD呢？（这位学生快速跑到讲台上，画出一个图形，证明王亮的证明不成立） 生3：我猜测，王亮同学一定是没有找到合适的方法解决这个问题，或者只是通过这道题目给定的图形相对比较特殊，使他误以为四边形ABMO为正方形，才犯了错误. 师：看来，如果给定的已知条件没有充分使用，那么，就可以断定解题错误. 不过，应该怎样证明这道题呢？ 生4：先逆向推理，假设AM为平分线，那么根据平分线的性质判断，BM=MO. 如何证明呢？根据已知条件，MN=MD，且∠MOD与∠MBN都为直角，如果能再求出∠BMN=∠OMD，就可以证明这两个三角形全等，进而推断出BM=MO. 师：有了两个条件，再找出一个条件，就可以证明它们全等了. 大家看，还有MN⊥MD这个条件没有利用呢！ 生5：明白了，利用矩形ABMO的性质和MN⊥MD这两个条件，可以推出∠OMD=∠BMN，这样就可以证明它们全等了. 师：对，这是“K型”问题. 该题涉及逻辑推理，跳跃性强，需要几个转换，具有多向性和多元性，要求学生具有较强的发散思维和综合运用知识的能力. 学生做题想到画辅助线，但是在利用辅助线并根据已知条件分析数学元素之间的关系时，存在一定的茫然性. 通过师生的共同诊断、分析，大家找到了病根，于是豁然开朗. 如果没有交流，出错的学生恐怕不能独立解决这个问题，且使大家丧失了一次宝贵的预防错误产生、锻炼分析错误的机会. 2. 集中纠正 对于典型错误，可以采取集中统一讲解的方式，给予纠正，这样可以更有效地利用错误，及时、高效地转化为教学资源，使错误的价值集成化. 比如数学常见的错误有：（1）概念理解模糊；（2）误解题意；（3）遗忘条件；（4）思路错误；（5）非技术性错误等，针对这些错误，可结合实际例题具体分析成因及对策. 案例2？摇 耿思亮为了帮助爸爸弄清楚日平均用电量，在10月份前五天，每天准时抄录电表，记录情况如下： 耿思亮同学给出了他一家10月总的用电量大约为：（122+127+133+136+142）÷5×31=4092（度）. 分析？摇 这位学生由于受思维定式的影响，没有结合生活实际情形，致使机械地按常规平均数的求解方法去审题、解题. 正解 （142-122）÷（5-1）×31=155（度）. 利用这个典型错误，可以有效地提醒学生要根据具体的数学情景，灵活地运用数学知识解决问题，而不能主观臆断. 除此之外，我们还应当要求学生自主整理典型的数学错误. “好记性不如烂笔头. ”指导学生制作典型错误题集，能够切实帮助学生避免再犯类似的错误，提高其分析问题的能力. 我们可以不定期地通过交流、抽查等形式，督促他们切实整理好. 我们本身也要不断地反思学生错题产生的原因，便于从源头上解决数学知识和技能传授上的不足. 荷兰著名学者弗赖登塔尔说过：“反思是数学的重要活动，是数学活动的核心和动力. ”反思的内容必然也包括数学错误. 因此，我们力求最大可能地使学生避免错误的产生，同时也要有效地利用好数学错误.
随便看	基于人工智能在公共管理中的运用 建筑施工企业税收筹划实施策略 党建引领多措并举推进乡风文明建设 从公共管理的视角分析社会保障私有化趋势 中小企业投资管理存在的问题及对策 政府采购项目招投标实施策略思考 消费者跨渠道购买行为影响因素分析 当前我国土地整理融资方式的选择与应用研究 工程咨询类项目全过程经营开发策略 中国现代管理理论 探究电力企业班组安全文化建设与实施 新时代关于健康中国战略系列论述的时代价值 人本管理思想在企业管理中的应用 领导干部使命意识培育路径探析 商品混凝土公司中试验室的作用及其管理探究 谈高校后勤管理信息化 政工工作对企业思想政治的推动作用 国有企业职工思想状况调查研究 校地党建合作的实践与探索 国有企业基层党建政工工作的加强措施 思想政治工作与医院人力资源管理相互关系的探讨 企业深化改革进程中提升党建价值创造水平研究 强化工会民主管理促进和谐企业建设 公司存货问题的研究 电力企业廉洁文化建设实践研究 ropey ropey, ropy rope² rope¹ ropier ropiest ropily ropiness ropinesses roping ropy roro ro-ro ros rosaries rosary rose rosebud rosebuds rose-colored rose-coloured rose coloured rosed roseless roselet 创造社 创造继承 创造进化论 创面 创： 刜 刜打 初 初一 初一、十五或间或吃斋 初一十五开的庙门早了——放出些小鬼来 初一十五的庙门早了——都竟出些小鬼来了 初一吃十五的饭——前吃后亏空 初一子，初二郎，初三初四女拜娘。 初一崽，初二娘，初三初四拜姨娘 初一的月亮 初七八的月亮——半边阴 初三 初中 初为孩子人子 初义 初九 初乳 初二 初二三的月亮——不明不白

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。