《浅谈离散数学的问题》-工学论文，计算机论文-论文范文参考-科学狗论文网

网站首页词典首页

标题

浅谈离散数学的问题

范文

摘要：离散数学是计算和信息学科的理论基础，知识点多且散，是学习和应用的主要障碍。本文通过细分离散数学问题的内容，划分了问题的类型，提出了问题的模式，分析了各种类型问题的主要特征和解题方法，提升了离散数学的系统性，降低了其学习和应用的难度。

关键词：精益学习;精益生产;模式;离散数学

中图分类号：G434? ? ? ? 文献标识码：A

文章编号：1009-3044（2019）23-0067-04

开放科学（资源服务）标识码（OSID）：

The Pattern of the Problem of Discrete Mathematics

CAI Guang-jun

（Henan Science and Technology University， Luoyang 471023， China）

Abstract： Discrete mathematics is the theoretical basis of Computing and Information Science. For the reason there are so many and scattered knowledge points in discrete mathematics， it is difficult to learn and use in reality. By analyzing the content of the problems of discrete mathematics， this paper presents the pattern of them. Each pattern puts forward the models of problems， analyses the main characteristics of the various types of problems and their solutions. These work can improve the systematic of discrete mathematics， and reduce the difficulty of its learning and application.

Key words： Lean learning; lean production; Pattern; Discrete Mathematics

离散数学作为计算和信息学科的理论基础，和很多现实问题紧密相关，应用广泛深入。离散数学又具有范围广、内容多的特征，各个部分独立性强，难以整体把握、形成可应用的知识模块。

本文从精益学习[1]理念出发，在5S方法[2]进行局部知识精益化的基础上，从整体上用模式归纳离散数学的问题。模式源于建筑[3]，引入软件后经[4]发扬光大，对程序设计理论具有重大的影响。为了克服模式多、方法杂的不足，[6]根据内容和关系类型进行模式得抽象提取，本文以離散数学[5]问题的类型和关系为基础，利用模式方法进行问题的分析归类。

首先讨论了问题的内容，以内容为基础把问题分为判定题、证明题、计算题和应用题四个部分，分析了每类问题的主要特征和解决方法。

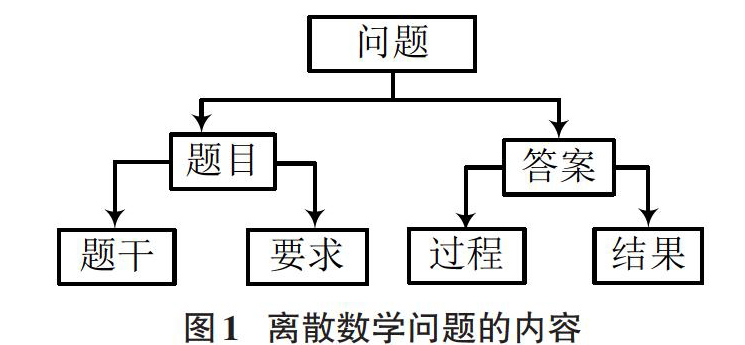
1 离散数学问题的内容

离散数学中问题的元素结构如图1所示，含义如表1所示。其中，题目是已有的内容，开始是实的;答案是对问题的解答，开始是虚的。

本文问题的分类主要依据要求和结果间的关系，它们间的主要区别如表2所示。其中判断题和证明题都有确定的结论或目标，关键是方法的选择，判断题需要确定是否或类型的选择、证明题则需要提供结论成立的依据;计算题虽然没有确定的结论，但是一般具有确定的规则和推导方法;应用题则不仅无法确定结论和方法，而且前提是什么，是否有方法解决都不确定。

每个模式分为特征、内容、类型、步骤、难点和示例6个部分，其中特征用以判断问题的类型;内容用以细化对问题的判断，分析问题各个部分间的特征和关系;类型用以细分问题，提供问题的解决的整体框架和策略;步骤是解决该类问题的关键步骤，难点是解决问题的核心;示例展示问题的特征和通用的解决方法。

2 判断题

判断题根据前提确定结论的类型。以“要求”是核心，题干具体、要求抽象、类型简单，外部知识少且较易确定，题目和答案之间、题干和要求之间多是一对一的关系。解题多从要求出发，是从具体到抽象的过程，可以看作对具体对象的分类。判断题可以实现性质或规律点到面的扩展，比如通过判断一个系统是群，则系统可以进行所有群的运算，具有群的元素和内部结构。

特征：题目的“要求”蕴含答案的“结论”，结论是“是或否”或是要求的类型之一;“题干”比“要求”具体。

内容：题目一般比较简单，题目中题干具体、要求明确;答案部分以结果为主、过程比较简单。答案具有确定的范围，解答所需知识范围小，和要求或题干直接相关，容易确定。题干比较具体，可以是某个对象、对象的某个性质或对象间的某种关系;要求比较抽象，是对对象、对象性质或关系的归类。过程通常比较简单，多来自要求的定义、定理;结论为“是否”之一或某些性质、关系、类型。

类型：根据要求是否包含结论，可以分为直接型和间接型两种。直接型的结论是“是”或“否”;间接型的需要在可能的性质、关系或类型中选择。是与否的判断直接从“要求”对应的定义、定理出发，分解、选择所需对比的内容;性质、类型和关系的判断要先确定可选择的选项，再根据选项的要求和题干特征选择合适的表示、性质进行判断。

步骤：判断题可以从正反两个方面解决，既可以通过相符判断是，也可以通过不符判断否。判断题的主要步骤有：分解、对比。分解是根据题目的要求对应的定义、定理把其分为多个局部的、具体的特征，最好是实现与题干的对应。对比是判断“要求”分解的结果与题干的内容是否一致。

难点：判断题多数比较简单，主要难在如何记住分解所需的定义、定理。

示例：离散数学中的主要判断题如表3所示。要求代表了问题，直接型的主要依据是要求的对象、关系或性质;间接型的主要依据是要求蕴含的选项。

3 证明题

证明是要为“要求”提供正面支持，即实现“前提+性质”到要求的转换。证明是由前提和外部知识为两端，选择中间内容及其次序、结构的过程。证明题的“要求”就是结论，以多对一和一对一的结构为主，过程的内容和变化规律难以确定。从问题形式可以分为恒等式证明，目标证明;从证明对象可以分为实体证明、性质证明、关系证明等。证明适合具有明确目标的问题，还可以通过对性质和关系的确立，获取新的定理来简化问题的处理，如握手定理的证明提供了判断度数序列能否成图的依据。

特征：题目的要求就是答案的结论，答案的中心是过程;题干和要求以抽象的内容为主。

内容：题目和答案以抽象内容为主，题目范围较广，题干是要求的前提，要求是题干的结论，两者可以是互为充要条件或题干是要求的充分条件（含外部知识）。答案的核心是过程，且具有两个相反的方向，思考时多是从后向前，即从要求到题干;书写时多从前向后，即从题干到要求。

类型：根据前提和结论的数量，证明题主要为一到一的和一到多两类。一到一;多到一。

一到一证明时前提和结论之间多是等价的，证明的关键是求同去异，可以采用从左到右、从右到左和从两端到中间的不同策略，依据从复杂到简单、从长到短、从杂乱到统一的原则，根据前提和结论的差异，先对前提进行拆分，再根据目标进行重组。

多到一证明时前提和结论存在大小、数量上的差异，需要进行组合和转换，组合的依据多是“要求”蕴含的结构、规则或题干不同元素之间的联系，转换是同一内容的形式变换是多个前提条件到单个结论的转换。证明时“一”是核心，证明的关键是根据“一”进行条件的选择和中间的排序，包括根据“一”的结构进行分解，选择元素并组合;根据与“一”的远近关系进行连接排序。

步骤：证明题的关键步骤有：分解，转换，综合。分解多是虚步骤，主要针对要求，也可以是部分题干，要求分解是实现问题从大到小的简化，并可以提供后期综合的依据;题干的分解是增加、提取所需的证据。转换主要针对内容相似形式不同的题干和要求之间或一些中间结果之间，关键是确定两者间的不同，利用相似性转换，导出结论所需的内容，舍弃结论无关的内容。综合是进行内容的结构合成，是多到一变化的关键，主要任务确定元素的位置和关系，动态可以根据内容的相关性（如逻辑推理时是否有相同的命题变项或子公式），静态主要根据“一”（如要求）的结构。

难点：证明题的难点是转换和分解，转换难在如何取舍不同内容的异同，分解难在如何使分解结果和题干对应。

示例：证明题考查的是对中间步骤的填充，如表4所示。1：1的典型是等值式的证明，依据公式的性质进行变换，求同去异;m：1的关键是确定多到1中内容的对应，实现多方内容的组织和综合。

4 計算题

计算是由已知求未知，是根据题干、计算规则和“要求”的含义确定答案的过程。计算题是规则和方法在具体内容上的应用。题干相对证明较具体，所需知识范围较确定，不具有可以对比的结果。计算题类型多样，可以从多个角度划分。计算题由于答案中结果和过程都不确定，导出结果的关键在于题目中蕴含的题外的规则。计算题是规则和方法的纵向应用，是已知到未知的转变，可以直接用于理论的转换和获取结果及本质。如求真值表可以确定命题公式的取值，求极大元可以确定满足要求的元素。

特征：答案中过程和结果都不确定;题目要求只确定了结果的要求，不直接包含最终的结果;答案过程对外部规则依赖大，范围选择较广。

内容：计算题无论内容和关系都比较复杂。题干是需要转换的内容、要求是转换的方向、外部知识是转换的原则。题目和答案内容以具体的为主，也有抽象的;答案既要求过程，也要保证结果;各个部分的内容既有实体的，也有关系和性质的;计算题对外部知识要求较高。

类型：计算题核心可以分三类：一是题目之外的规则，二是题目的要求，三是题干和要求一起作为核心;数量上有一到一的、一到多的和多到一的;大小上有同级的、大到小的和小到大的。规则为核心的，多是多到一的，大小以同级的为主，解题时多采用从题干出发选择规则，根据确定的计算方向、优先级和结合性进行到结果的转变;要求为核心的，多是多到一的，大小以从小到大的为主，解题时多从要求确定解题的规则和方法，然后根据规则和方法对题干进行组合或转换;核心是题干和要求一起的，多是一对一的或一对多的，大小为同级或从大到小的，解题时多从要求出发确定目标，再对比题干和目标的差异，根据差异确定由题干导出结论的方法。

步骤：计算题的大步骤可以分为三步：分解，转换，综合。

分解针对题干和要求数量、粒度上不对等的问题，是根据定义、定理的分解，包括要求、题干或中间结果的分解。要求的分解是问题的化简、规则或方法的提取，通过分解把一个大问题分为多个小问题、再根据各个小问题的要求确定题干的变化原则，多是该类问题的起点;题干的分解是为了提取要求所需的直接或间接元素，去除要求无关的元素;中间结果的分解根据位置不同可以具有题干分解、要求分解或同时兼具两者的特征。

转换多时针对内容相同、形式不同的问题，转换的关键是确定题干和要求或其内容之间的对应关系，根据被转换对象和转换结果之间概念之间的相同点和形式不同确定形式上的对应规则和方法，然后根据规则进行被转换对象的转换。

综合是分解的逆反，问题特征与分解相似，但方向不同。包括基于目标的综合和基于题干的综合，前者是根据目标对象内容、结构和性质要求，确定需要综合的元素和元素之间的关系;后者是根据题干相关的外部规则，确定题干不同内容或其元素之间的关系。

难点：一是结果不确定，题干、要求、过程都不含结果的直接形式;二是过程的构建在题干之外;三是类型多，不同类型解决方法不同。

示例：计算题的解决是由题干+外部知识导出答案的过程，关键是确定题干和要求之间的关系和外部知识的选择，典型代表如表5所示。影响较大的是题干元素和要求之间的关系，包括大小和数量关系，大小相同、数量一对一多是转换的问题;前大后小、一对多的多是分解的问题;前小后大、多对一的多是综合问题。

5 应用题

应用题是知识和方法在自身领域之外的使用，是知识在现实中的使用能力的考验，包括问题的转换和一个或多个判断、证明或计算的过程。应用题不仅不具有确定的过程和结果，所需要的知识、方法的内容和范围不确定。可以分为根据要求确定知识的直接应用和根据题干确定知识的间接应用，前者目的明确，通常是单次应用;后者可以多次应用。应用题是规则和方法的横向应用，可以直接解决现实问题或扩大知识的应用范围。如求最短路径可以确定两点的最短距离，求最小生成树可以确定城市间的最小连通成本。

特征：题目和答案没有直接关系，题目内容在所用知识之外，甚至在离散数学之外，答案过程和结果不确定性更大。

内容：题目范围更广，题干可能含有与解题或结果无关的信息，要求可能是判断、计算或证明的任一类型，现实中题干和要求还具有不确定、不完整或冗余等特征。答案中不仅含有解题过程，还包括题目与方法间的转换过程。答案和题目没有直接关系，主要根据题干与表示方法，要求与解决方法之间的相似性进行尝试判断。

类型：根据求解问题类型的不同，可以分为直接型和间接型两种。直接型应用题中方法与要求可以一一对应，主要用于解决单个或一类问题，根据要求的特征确定所需的知识、方法和解题过程;间接型应用题方法与题干具有相似性，先转换为方法的理论，再寻找解决方法和答案。直接应用是已确定需要解决的问题，利用目标知识或方法和问题间的对应关系直接解决;间接应用是先把具体对象转换为目标方法中的对象，再运用相关方法确定需要解决的问题和解决方法。

步骤：应用题的大步骤可以分为三步：对比，转入，求解，转出。对比是通过比较题目和各种方法之间的关系，确定解题所需的方法，不一定出现在答案中，却是解题的关键。转入是实现题干（部分含要求）到方法表示之间的转换，把题目中问题转换为具体方法可以解决的问题。求解基本是包含一个完整的判断、证明或计算过程，是答案中过程的核心。转出是把求解结果转换为问题的答案的结论，通常比较简单。

难点：应用题的难点是对比，对比的关键是确定所需要的理论知识，它的选择不仅确定了结果是否正确，还决定了过程的对错和效率。

示例：应用题的解决从要求出发，看是否直接蕴含了所需的方法或理论，否则再看是否能根据题干一起确定，典型例子如表6所示。

6 小结

总的来看，离散数学不同类型的问题间内容、外部知识和核心间的区别比较明显，如表7所示。结果和过程的导出都有一定的规则，且通常长度不大，主要难在概念多，范围广。判断题重结果、证明题重过程、计算题两者并重;应用题则是三者的综合，是问题的转换，可以细分为判断应用、证明应用和计算应用。

本文用模式总结了离散数学的问题，提供了一种新的认识学习离散的纬度。虽然本文只是离散数学问题、表示、方法、化简等内容的第一部分，其效果和使用方式即使在离散数学中还有待进一步验证，但本文得方法和原则却不限于离散数学，它可以作为一种新的知识提取模式实现对各个学科高層知识和内在方法进行提取，为素质提升和能力培养提供了新的内容和方法。

参考文献：

[1] 蔡广军. 精益学习初探[J]. 教育现代化， 2017，4（7）：28-30.

[2] 蔡广军，付海，王书通，吕鹏云. 精益5S方法在离散数学中的应用[J]. 电脑知识与技术，2017， 13（1）：112-114.

[3] Alexander， Christopher;Ishikawa， Sara; Silverstein， Murray; Jacobson， Max; Fiksdahl-King， Ingrid; Angel， Shlomo. A Pattern Language： Towns， Buildings， Construction[M]. New York： Oxford University Press.1977.

[4]E. Gamma， R. Helm， R. Johnson， and J. Vlissides. Design Patterns： Elements of Reusable Object-Oriented Software[M]. New York：Addison-Wesley Professional， 1994.

[5]屈腕令，耿素云，张立昂.离散数学[M]（第二版）.北京：高等教育出版社， 2008.

[6]蔡广军.基于环境建模的服务组合方法[D]. 北京：中国科学院计算技术研究所， 2011：61-74.

【通联编辑：王力】

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。