《Grasshopper在建筑中关于渐变表皮的运用研究》-工学论文，计算机论文-论文范文参考-科学狗论文网

标题

Grasshopper在建筑中关于渐变表皮的运用研究

范文

覃庆贵　饶斯瀚

摘要：文章以grasshopper为基础，探究渐变表皮在建筑上的运用。文章首先研究表皮在二维平面的生成，重点研究生成渐变的精确控制方式。其次，研究表皮从二维转化到三维的方法和思路，具体通过检验建筑表皮在二维表皮在比较简单、方正的造型中是否成立，然后再检验在曲面造型中是否成立。在此基础上，重点分析建筑表皮在不同形式建筑上产生的方法。

关键词：Grasshopper;建筑;渐变表皮

中图分类号：TP391? ? ? ?文献标识码： A

文章编号：1009-3044（2021）01-0240-02

Abstract： Based on grasshopper， this paper explores the application of gradient skin in architecture.Firstly，thispaperstudiesthe generation of skin in two-dimensional plane， focusing on the precise control of generation gradient. Secondly， this paper studies the methods and ideas of the transformation from two-dimensional to three-dimensional skin.Specifically， Check whether the building skin can be used in the two-dimensional skin in the square and curved surface modeling. On this basis， it focuses on the analysis of the methods of building skin in different forms of architecture.

Key words：Grasshopper; Architecture;Gradual skin

“渐变”是一种以“重复”为基础的变化构成，它的相邻的变化型之间有种较多的共同点和联系，通常渐变型是对基本型的一种有规律地深入或者简化。渐变构成常常追求的是给人一种视觉上的动感，具有很明显的活跃性。设计构成中的渐变构成常常显示出渐增渐减进展的速度感，渐变的速度太快容易失去渐变所特有的规律性效果，会给人不连贯的感觉，渐变得太慢又会给人一种重复的感觉，不管是太快还是太慢都会让渐变的效果大打折扣，所以在做渐变表皮的过程中要数值的精确调控非常重要。渐变的方式有很多种，例如从形象上有形状、大小、色彩、肌理等，这些渐变在grasshopper中基本可以实现。这里主要以常用的是大小、位置的渐变为例，研究最具明显规律性的建筑表皮渐变。

1 grasshopper在平面生成渐变表皮

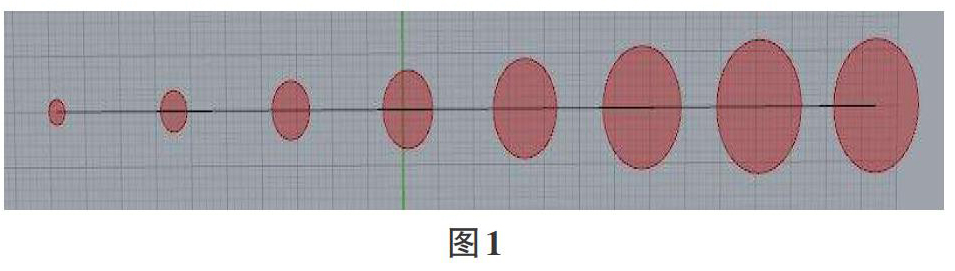
无论多么复杂的建筑表皮，其最开始都是以二维的形式出现。所以，建筑表皮的设计，最开始一般要从平面着手去分析渐变表皮的基础结构，然后设计结构形体。而grasshopper则可以以参数化的形式来处理进行建筑表皮的设计。下面以一个圆的渐变为例。

第一，定义基本结构点，这里就是圆心。首先，任意定义一条线，并与Curve运算器相关联。接着运用Divide Curve运算器，将关联好的直线进行等分，以等分的点作为圆形表皮的圆心。

第二，也就是核心步骤，即产生渐变。具体而言，就是通过圆直径数值的变化来产生渐变。最简单和最常用的方式就是运用series运算器，它能夠产生等差数列的渐变。其s值控制起始直径大小，n值（差值）决定变化的剧烈程度，c值决定变化数量。在这当中，s与n值根据不同的设计而给予不同的数值，但c值的数据是与运用List Length运算器与之前结构点（这里的圆心）的数据相匹配的。

需要特别注意的是，在渐变中，并不一定是等差数列的渐变方式，还有其他的如正弦函数、指数函数、等比函数，甚至任意曲线等渐变方式。而产生这些渐变，就需要用到核心Evaluate运算器。其E输入口可以输入任意数学公式。在grasshopper中可以任意设置多个自变量式的输入，以做等差数列为例，可以直接输入Sn=n*a1+n（n-1）d/2的表达式。但实际上，表达式的a1、d、n值分别对应series运算器的s、n、c值，二者起到的效果是一样的，这也意味着，在产生渐变的程式中，Evaluate运算器完全可以取代series运算器进行任意函数公式的渐变。

最后，把平面的图形转化成面体快。这里就是把圆，形成一个扁小的圆柱。主要运用到面生成的运算器，如loft、Swp1运算器，把圆放样，然后用cap运算器封口就完成了。（图1）

2二维表皮运用于三维建筑模型中

在参数化设计中，任何一个表皮的程式都应当适用于各种建筑模型。一般而言，至少能够适用于二大类，一类是方方正正的没有曲面的，一类的曲面或异形。在参数化设计中，首先考虑的是二维表皮在比较简单、方正的造型中是否成立，然后再检验在曲面造型中是否成立。

2.1建筑表皮在方形造型中的设计

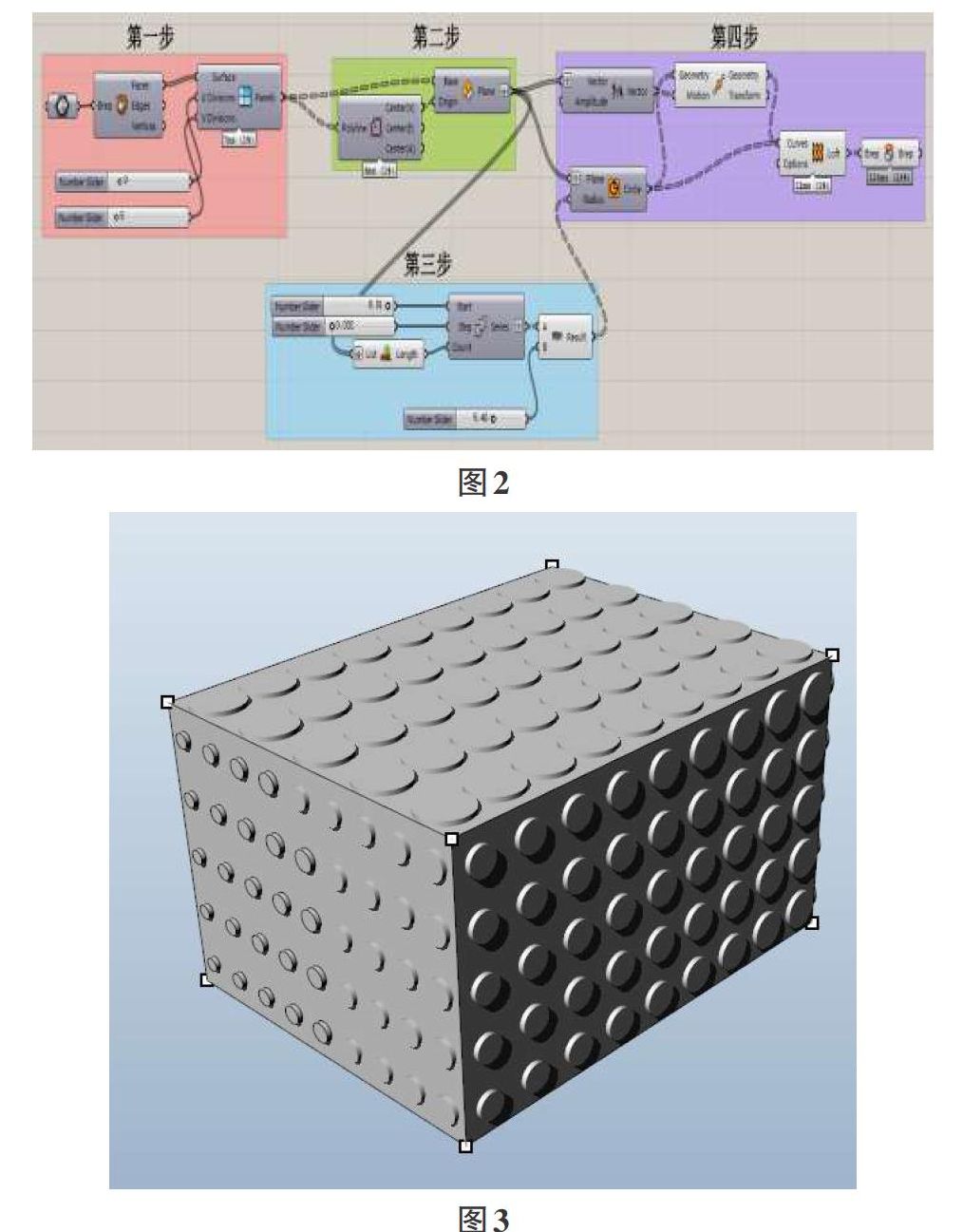
要确定设计的二维表皮是否能赋予建筑，首先考虑他在一个建筑矩形造型下是否成立。这里以任意一个立方体为例。（程式见图2，效果图见图3）

首先，在Grasshopper中设计任意一个立方体。接着，重点在于将立方体进行线面的细分。因为所有表皮必须在细分的线面上按原二维逻辑重新产生。这里要运用到二个经常关联的运算器，一是，Deconstruct Brep运算器，可以将物体分解为点线面，二是将LunchBox命令下的Panels命令组，其下所有命令都是对模型的细分方式。通过这2个模块，原造型得到了新的，适合与表皮生成的细分方式。接着，根据得到的细分，取用所需要的结构。这里为例，需要取用的是结构面的中心点。主要运用PolygonCenter运算器。将Quad panels运算器的输出端与Polygon Center运算器的输入端相连接。

其次，也是二维表皮转化为三维最为重要的，定义每个点在曲面上的方向。由于一个三维建筑造型细分之后，每一个小面的xyz坐标都是不一样，所以必须根据每个小面自己的坐标进行表皮的生成设计。即需要取出结构点（这里的中心点）后就由结构点重定义平面，这里用到的是Plane Origin运算器。在将Quad panels（Quads）运算器的输出端与Plane Origin运算器的B输入端相连接，再将Polygon Center运算器的Cv输出端与Plane Origin运算器的O输入端相连接。这样，每个结构点与每个细分面的就形成了对应关系，而参数的相互关联，这可以说是所有参数化设计的核心。

再次，重定义平面完成后再由它与前面做好的基本型运算程序相关联。将Plane Origin运算器的输出端与Circlc运算器的P输入端相连接，以控制圆心。Circlc运算器的R端则与series运算器相接，以控制直径，并且产生渐变。这里，值得注意的是，在实际渐变中，不一定是从小到大一直渐变，可能大到一定的值，就不能再大了，因此，可以用min运算器对直径予以控制。

最后，平面的圆形表皮产生厚度。运用move和loft运算器可以算出圆凸出厚度，然后用cap holes运算器封口就完成了。需要注意的是，move运算器的方向在之前Plane Origin运算器已经求出来了，移动厚度的方向就是Plane Origin的pl输出方向。

2.2建筑表皮在曲面造型中的设计

当一个表皮设计在矩形造型中能够成立，那么如果在曲面造型中也可以适用，就基本上意味着这个表皮可以适用于各种造型的建筑。这里，以一个圆柱为例，研究渐变表皮在曲面造型上如何适用。

首先创建曲面建筑的基础结构。Circle运算器画圆，接着运用Move运算器控制结构，loft放样，基本柱体就设计完成了。接着，对整个建筑模型的细分。这里，即对圆柱的细分。同上，取用Deconstruct Brep）运算器和Quad panels运算器。这里与方形建筑的细分方式类似。

其次，也是最为重要的，根据细分后的面再重定义平面。这里与之前不同的是，考虑到是对曲面的划分，划分出来的面有可能是曲面，即意味着每个细分的曲面上的结构点与面垂直的那个向量方向都是不一样的。而表皮的设计却需要能有一个统一的参数或模块对其进行控制，达到任意曲面上点都可以与曲面垂直。因此，这里运用Surface Closest Point运算器和Evaluate Surface运算器来重定义平面，这2个运算器一般搭配使用。Surface Closest Point运算器接s端接收任意曲面，而p端接收任意点，输出的是接收到的点垂直投影到曲面上形成的并具有UV坐标的投影点，即uvp输出端的点，这样就保证了点与面的垂直。接着，搭配Evaluate Surface运算器，vu端接Surface Closest Point运算器的uvp输出端，s端接原细分的曲面。这样，EvaluateSurface运算器就能输出所需要的方向向量。这样，基本上完成二维到三维的转化。到此，在这个案例里，还需要把向量方向垂直的XY平面设定出来，因为每个点的XY平面都不一样，但都与求得的方向向量垂直。即还需要把Evaluate Surface（EvalSrf）运算器的N输出端与Plane Normal运算器的Z输入端相连接，运用Plane Normal运算器把垂直面也求取出来，这样重定义平面就完成了。之后二步的设计方式与方形造型相同，这里就不在阐述了。

3小结

参数化设计，简单地说就是建立某种特定的关系，当这种关系的某个基本元素发生变化、其他的元素也随之变化，因而参数化的重点是彼此元素之间的关联性。而在建筑的表皮渐变设计中，有二组非常重要的关联参数，一者，就是运用Evaluate或series运算器进行函数表达而产生可控制的精确渐变变化;二者，就是在各种建筑表面生成渐变表皮时，结构点的XY平面与建筑表面的对应关系。设计好这二者的关系，就能实现任意渐变表皮在建筑中的运用。

参考文献：

[1] 白云生，高云河.GRASSHOPPER参数化非线性设计[M].武汉：华中科技大学出版社，2018：98.

[2] 程罡.Grasshopper参数化建模技术[M].北京：清华大学出版社，2017：68.

[3] 王奕修.Grasshopper入门&晋级必备手册[M].北京：清华大学出版社，2013.

[4] 帕特里克·舒馬赫，徐丰.作为建筑风格的参数化主义——参数化主义者的宣言[J].世界建筑，2009（8）：18-19.

【通联编辑：梁书】

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。