《基于图像纹理的假币快速计数方法》-工学论文，计算机论文-论文范文参考-科学狗论文网

标题

基于图像纹理的假币快速计数方法

范文

张辉陈勐翔

摘要：设计了一种基于图像纹理信息的假币纸张计数方法。预处理阶段，先对排列整齐成叠假币的图像进行灰度化处理，再利用拉普拉斯锐化增强假币纸张边缘信息，而后进行自适应阈值二值化处理得到假币纸张条纹图;纸张计数阶段，根据假币纸张边缘区域像素0、1变化的特点，快速、多区域地统计假币二值化图像中反映纸张数目的亮纹理信息，并投票给出假币纸张数目。实验结果表明，该方法能快速、准确地实现假币纸张计数，方法简单且对轻度噪声不敏感。

关键词：拉普拉斯锐化;二值化条纹;纹理信息;纸张计数

中图分类号：TP391.4 文献标识码：A 文章编号：1006-8228（2020）09-76-04

0引言

制贩假币案件中查获的假币需计算数量用以量刑，在实务工作中查获的假币往往数额巨大但纸张码放整齐。目前，案件中对假币计数的方式一般采用点钞机计数的方式，但这种方式存在计数时间长、设备易损坏、假币纸张易破损等缺点。设计一种无损、快速、准确的假币计数方法具有一定实用价值。

国内外已有许多同类型计数方法的研究，其中相关性最大的是关于纸张计数方法研究。石伟等设计了一种基于灰度差分的纸张计数算法，采用纵向灰度投影法得到灰度曲线并进行灰度差分计算，根据灰度像素曲线波峰与波谷的具体位置判定纸张数目。苗良等采用类似方法，通过LOG滤波获得纸张图像的二值化边缘图，而后采取灰度差分及差分统计法计算纸张数。刘颖通过对纸币图像的条纹预处理、Gabor滤波增强边缘、p率阈值分割去除多余条纹、条纹校正等措施获取较清晰的条纹图像，并选取三段子图像计算，最终投票得出纸币数量。王富治等对图像极值区域和非极值区域进行0、1标记获得二值化条纹图像，从而计算纸张数量，相比阈值选取获得二值化条纹图像，有更好的抗毛边、抗光照不均等性能。李毅等对采集的层叠纸张图像，分别通过二维Gabor滤波器处理和逐行频率分析提取纸张边棱条纹，从而计算纸张数目。梁海毅等同样从纸张侧面图像明暗交替的纹理特征入手，统计灰度曲线波峰数目计算纸张数。此外邱华林等提出了一种基于纸张图像中灰度曲率及峰值检测相结合的纸张计数方法，对于厚度O.05-0.2mm纸张计数误差都小于0.01%。总体来看，这些方法精度较高，但计算方法较为复杂，计算时间.也较长。

本文在前述研究基础上设计了一种基于图像纹理的假币纸张计数方法，直接统计二值化图像中0、1像素变化的频次，方法简单，能快速计算成叠假币的数量，同时非接触式的计数方法能够最大程度避免对证据的污损。

1假币纸张图像采集及特点分析

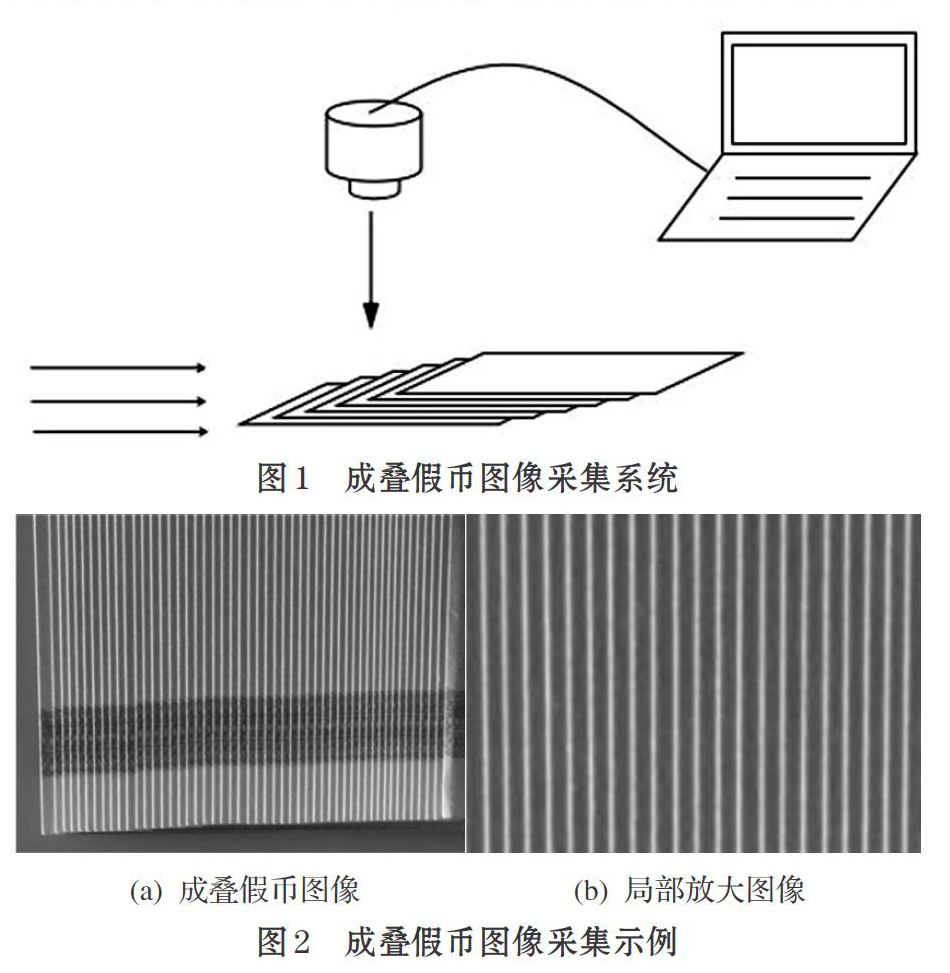
本文根据现实工作的特点，设计如图1方式的图像采集系统，其中假币实际由练功钞替代，其纸张厚度与常见的假币及真钞厚度基本一致，约在0.1mm左右。先将假币有序整齐叠放至平整、无污染的灰白色载物台上，假币纸张由下往上每两张间约有0.3-0.5mm缩进，这可通过分钞手法简单实现，从而提高假币纸张边缘间隔。同时为提高纸张边缘对比度，在载物台侧面使用平行光源掠入射照明。相机为装配微距镜头的单反相机，直接固定在三脚架上，垂直采集的图像實时传输至计算机端，用以后续处理。此系统面对需大量采集图像的场景时，无需实时更改硬件设置，具有较好的实用性。其采集的图像效果如图2所示。

观察图2成叠假币图像及局部放大图像可以发现，整齐的成叠假币纸张边缘线间相互大致平行，且接收光强更强，在图像中呈规律出现的亮条纹，而非纸张边缘区域接收光强较弱，在图像中呈间隔的暗条纹。因此从图像纹理特征上看，基于上述系统采集的成叠假币纸张图像为一幅具有明暗条纹交替变化纹理的图像，且亮条纹数即假币纸张数目，即便图像受到一定噪声的污染，这一特点依旧非常鲜明。如果能根据这一特点，实时统计采集图像中的亮条纹数，即可快速计算假币纸张数目，进而根据假币面额得出总涉案金额。

2假币纸张计数算法设计

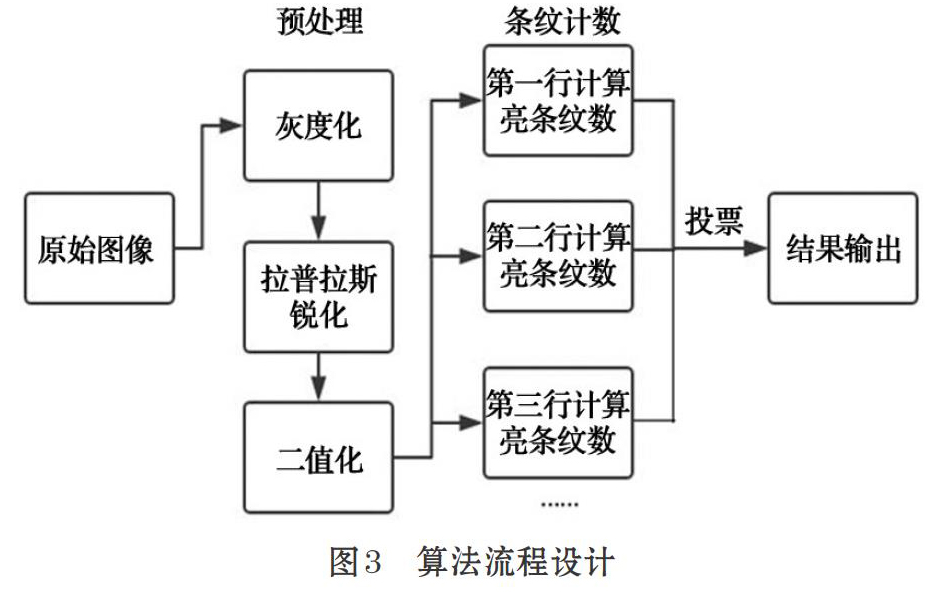
本文根据系统采集得到的图像具有明、暗条纹交替变化特点，设计如下假币纸张计数算法：首先，对成叠假币纸张图像进行灰度化操作;而后对纸张边缘区域进行拉普拉斯锐化处理，提高明暗条纹对比度，因明暗条纹特征受噪声干扰不明显，本算法不设计去噪环节;接下来，对增强后的图像进行自适应阈值二值化处理，得到二值条纹图像，此步骤可基本消除轻微噪声点的影响，且因为边缘线接收光照较纸张表面和载物台背景远强的特点，可以较好分割出边缘亮线;最后，直接在二值化图像纹理区域随机选取N行像素，统计各行像素0、1值变化的频次，得到亮条纹数，即假币纸张的数目，数目值出现次数最多者输出为最终结果。流程设计如图3所示。

2.1图像灰度化

采集的原始假币纸张图像为RGB图像，通过将RGB图中红绿蓝三通道的分量值加权平均计算得到该像素点灰度值。数学表达如式（1），其中Gray表示计算后的灰度值，R、G、B表示红、绿、蓝通道分量值。

2.2拉普拉斯锐化

本文方法主要以统计假币纸张边缘和表面交替变化的纹理信息来确定假币纸张数量，且主要是记录边缘亮线的信息。因此，对图像边缘信息进行增强有利于提高计数准确率，本文采用经典的拉普拉斯锐化算子对假币纸张图像的细节信息特别是边缘信息进行增强。

将拉普拉斯算子掩模对图像进行滤波操作，所得图像与原图叠加即可得到锐化结果图，锐化前后图像如图4示例。可见，尽管锐化也一定程度上增强了噪声，但相比假币边缘对比度增强的效果并不明显。

2.3自适应阈值二值化

随后，对锐化后的图像进行自适应阈值分割，自适应阈值选择方法是常见的迭代选择法，其迭代规则如下。

（1）初始化阈值为T。

（2）根据阈值T，将输入图像分割为像素值低于T的A集和像素值高于T的B集。

（3）计算所有处于A集和B集内像素点的灰度平均值t1，t2。

（4）根据t1，t2更新阈值：（5）重复计算第（2）-（4）步，逐步收敛至最终阈值。

根据上述步骤计算得出阈值后，即可进行二值分割，得到假币纸张条纹图像如图5所示。

放大二值条纹图像如图5（b），可发现像素值从0至1跳变一次即为纸张数目增加一张，噪声点基本与纸张边缘线粘连，不影响0至1像素变化的次数，从而对纸张计数影响降至最低。

2.4条纹计数

条纹计数针对前述处理得到的二值条纹图像来进行，其基本逻辑简单，有如下方法。

（1）从图像行数值中随机选择N个数值，得到随机计算亮条纹数的N行，N取合理整数。

（2）对于选取的每一行像素，遍历每一列像素，如某像素点灰度值为1，且其前一列像素点灰度为0，后一列像素点灰度为1，则标记假币纸张数目增加1张，确保每一条亮条纹只被计数一次。

（3）对随机的N行像素分别计算得到假币纸张数，分析形成的N维数组中出现次数最多的数值，输出该值即为假币纸张数，即投票决定最终结果。

计数方法流程如图6所示。

3实验结果及分析

为验证方法对成叠假币纸张能否准确计数，本文对数量为50张，100张，150张，200张的四组成叠假币分別进行了100次测试，计数算法运行环境为MATLAB，N取10。部分测试结果如表l所示。

根据测试结果可知，假币纸张数量在50张和100张时，准确率可达99.98%以上，100测试中各有一次测试值分别为49和99;假币纸张数量在150张时，漏检的测量次数增多，而假币纸张数为200时，测试平均准确率进一步下降。单次测试用时较快，如纸张数为100时，平均单次测量用时0.23秒，达到了快速计数的目的。分析纸张数增多时准确率下降的原因，主要是纸张边缘间隔减小导致条纹粘连所致。此外，在成叠假币厚度增加时，因普通微距镜头拍摄时景深不足而导致部分边缘线虚化，从而漏检。

4结束语

本文从实际出发，设计了一种快速、准确的假币纸张计数方法，该方法简洁有效，对采集图像进行灰度化处理，再进行细节增强，而后进行自适应阈值二值化处理，在得到的条纹图像中直接搜索亮条纹数目，从而得到假币纸张数量。同时，本文还设计了一种简易有效的成叠假币图像采集硬件方案。实验测试结果表明，方法在假币堆叠有序、单次计数张数不超过100张情况下，准确度很高，可适用公安实际工作。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。