《多源航迹数据融合系统的模糊关联算法应用研究》-工学论文，计算机论文-论文范文参考-科学狗论文网

标题

多源航迹数据融合系统的模糊关联算法应用研究

范文

黄涛水孝敏

摘要：随着我国民航事业的高速发展，为空中交通管制提供数据的通信导航监视设备种类和数量越来越多，如何将多源数据更有效地进行融合处理成为迫切需要解决的问题，本文针对其中核心算法之一的航迹关联，从处理架构设计、算法原理和评价准则入手，详细描述了模糊关联法的具体应用方法，并对测试结果进行评价后给出了基于参考目标拓扑矩阵的改进算法，最后对需深入研究的内容进行了探讨。

关键词：多源数据;数据融合;模糊关联

中图分类号：TP393? ? ?文献标识码：A

文章编号：1009-3044（2021）16-0005-03

开放科学（资源服务）标识码（OSID）：

空中交通管理通常依赖多源航迹数据经融合后形成的系统航迹来实施管制。目前大中型空中交通管理自动化系统接入的航迹数据不仅数量多且种类也较多，如一/二次监视雷达、ADS-B、场监雷达和多点定位等[1]。如果监视源数据质量下降（诸如交织交叠、反射、丢点和遮挡等异常）将影响管制运行效率，甚至会危及飞行器安全，因此研究并改进多源航迹数据融合系统显得尤为必要，多源航迹关联算法是其中关键的核心算法之一。

1 系统处理架构

为了有效地验证各个算法模块，必须设计一个适合本系统实际数据源的处理架构，通常有三类[2]：

1）集中式：同一时刻的所有数据发送至融合中心进行处理，好处是融合性能最优，缺点是中心运算负荷大、通信带宽高;

2）分布式：先各自进行航迹处理后将本地航迹发送至融合中心进行处理，好处是中心运算负荷小、通信带宽低、鲁棒性高，缺点是原始信息有所缺失，在一定程度上降低了融合性能;

3）混合式：兼具上面两类的优点，对中心的运算能力和通信带宽都有比较高的要求，但从能效比综合考虑是最好的。

图1给出了本系统采用的混合式处理架构：

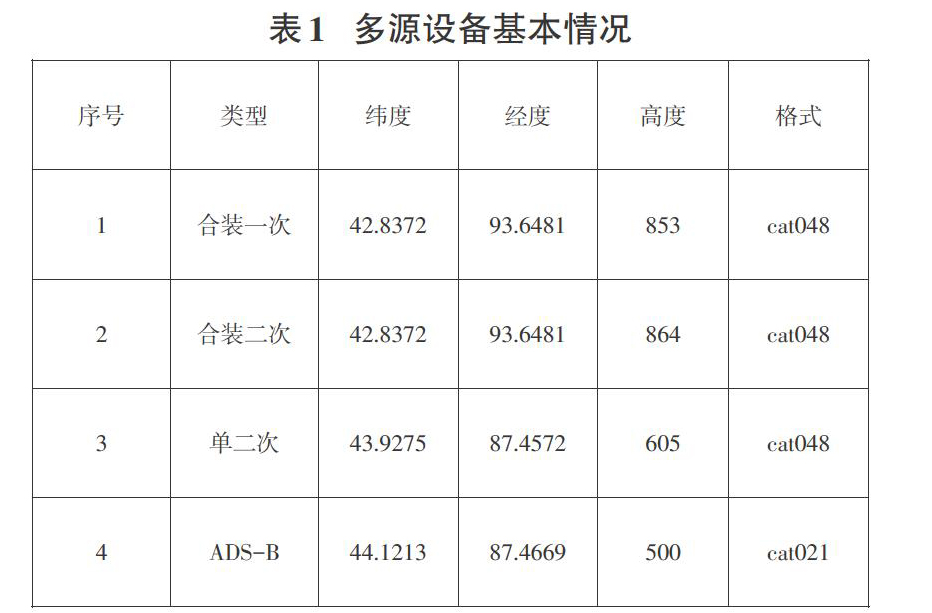
表1为测试数据来源的新疆4部设备基本情况：

2 航迹关联

航迹关联的实质是航迹匹配，由于存在多种不确定性，包括各设备自身的系统误差、随机误差以及来自内外部的杂波干扰，都将带来匹配问题。

经典的航迹关联算法大多以假设传感器数据通过滤波或标校后只含观测噪声，算法得到的是基于此假设的多传感器数据集合的最优匹配结果，基于统计理论的最近邻域法、贝叶斯法和D-S法等[3]，利用经典的状态估计及协方差矩阵等信息确定关联匹配，但是在多个观测目标聚集或虚警较严重时，可能会出现关联错误或遗漏情况;引入模糊理论后，多观测目标间的位置、速度、航向的差异都可作为新因素，在一定程度上解决关联算法中各种偏差导致的模糊性问题，为适应多源航迹融合所面临的复杂环境中关联问题提供了一个很好的解决思路。

3 关联性能的评价方法

评价方法选用了模式识别中使用的Precision-Recall-F1方法[4]，具体如下：

TP：真数据已关联，目标匹配正确;

FP：真数据未关联，新目标;

TN：假数据已关联，目标匹配错误;

FN：假数据未关联，虚警;

Precision = TP / （TP + FP）;

Recall = TP / （TP + FN）;

F1 = 2*Precision*Recall/（ Precision+Recall）

Precision给出关联的正确率，Recall给出正确航迹的识别成功率，F1给出综合性能。

4 模糊航迹关联法

模糊航迹关联为关联过程中各因素分别确定隶属度函数以表征待关联航迹对在该因素的关联度，总关联度为各个因素关联度的加权和。该判决结果由模糊因素集合[Ukk=1，k][Ukk=1，k]，组成，各因素对应的隶属度函数（典型函数包括正态型分布，居中型分布，降T型分布等）定义为[μkukε0，1]，加权系数为[ak]，且满足[kak=1]，最终各航迹之间的相似度[Si，j]为[kakμkuk]，对来自[K]部雷达的所有航迹便构成了当前时刻下的[K]阶模糊关联矩阵。有了矩阵后，便可寻找最佳的全局解，我们采用的方法是最大综合相似度判别准则，具体步骤如下：

1）寻找矩阵中最大的元素[Si，j]，如果大于门限值，则可判定航迹[i，j]为关联对;

2）消去该元素所在的行列，矩阵将下降1阶;

3）重复1）和2）直到矩阵全部消去。

在此方法中，每个因素的加權系数体现各因素的影响程度，所以因素和隶属度函数的选取是应用中需重点关注的内容，我们选取了位置、航向和航速构成模糊因素集，正态型分布型为隶属函数，将时间段为1个小时的3组数据进行测试，结果如表2所列：

从F1可以看到在不同的时间段差异较大且不够理想，但模糊航迹关联方法最大的好处就是对各因素没有做任何限制，这就为我们在关联判决过程中利用更多的信息因素提供了改进的空间。

5 改进的模糊航迹关联法

5.1 方法概述

针对系统偏差较大且受到一定干扰的航迹关联场景，我们引入新的因素——目标参照拓扑，即待关联飞行器周边的其他飞行器作为参照物，利用他们之间的空间拓扑信息通过模糊航迹关联方法在处理此类非高斯分布的因素，可实现更好的航迹关联效果。

5.2 提取拓扑矩阵

为描述参照物的拓扑矩阵，需对参照拓扑进行提取，即构造参照物的拓扑矩阵。对于一个待关联目标，按照设备观测目标的特点确定采用什么样的坐标系，且维度最多可定义为三维。我们按照雷达的特点，以目标为中心，设定极坐标区域进行划分：沿直径等分S个圆环，方位等分T个扇区，这样参照区域就由S*T个单元组成。拓扑矩阵中元素值将对应单元目标存在可能性，为每个单元[Rij]分配适当的隶属度[Uij]，i、j分别为径向和方位的划分，通常约定该区域无参考目标时[Uij]为0，对应区域存在参考目标时0<[Uij]≤1。图2表述划分的示意过程：

5.3 拓扑矩阵的弥散化处理

随机误差（如系统差和观测噪声）是待关联航迹不确定性的主因。通常航迹经过数据源本地标校和滤波处理后，上述不确定性的影响已经大大减小，只要单元大小设置合适，待关联航迹对的位置应在同一单元内，拓扑矩阵就不会改变。弥散化处理降低了随机误差对航迹关联性能的影响。

航迹间的方位偏差反映矩阵中同一行的相邻位置上，且无论参照物在极坐标上的距离如何，落入同行相邻单元的可能性基本相同。距离偏差于此基本一致，不同的是反映到列上。

為应对此问题，需对拓扑矩阵做弥散化处理。当矩阵中的某一单元值为1时（即确定存在目标），需在其周围单元增加弥散化系数m（0

图3? ?弥散化过程示意图

5.4 基于拓扑矩阵的模糊关联

经弥散化后的拓扑矩阵实质上是参照目标在空间拓扑信息抽象成一种模糊数学表达，航迹关联就是将待关联航迹对的拓扑矩阵进行关联度（即相似程度）计算，找出最为匹配的航迹对。

考虑计算的方便性，将矩阵的第t行放在待观测目标向量的第t个分量上，在k时刻，[va]，[vb]分别表征雷达A，B的待关联航迹拓扑向量集中的任意两个向量，即代表两部雷达同时刻观测到的任意两条航迹。由此获得关联度函数如下：

关联度的大小反映两条航迹相似程度，经过弥散化后，如果两个参照拓扑中目标不在同一单元内，尽管相隔很近，关联度仍然不为0，为简单起见以两个单点拓扑（即只包含一个参照目标）举例说明，分两种情况计算关联度：

（1）两点间隔为1个单元

[νa=0，0.1，1，0.1，0]? [νb=0，0，0.1，1，0.1]

[Sνa，νb=0.196]

（2）两点重合

[νa=0，0.1，1，0.1，0] [νb=0，0.1，1，0.1，0]

[Sνa，νb=1]

此时可设定一个门限值[St]，当[Sνa，νb

6 思考

通过对基于参考目标拓扑矩阵的改进型模糊关联算法的实现机理和实际应用过程的应用与分析，我们认为有以下几个方面需要关注：

1）参考目标拓扑区域的确定

在拓扑中的参考目标数越多，可提供的拓扑信息就越丰富，匹配过程中获得的相似度的可信程度就越大。但当单元格固定时，参照区域的扩大会导致计算量的增加，如何平衡运算负荷与系统性能值得进一步研究;

2）拓扑单元格的划分

单元格划分的精细程度实际上决定了系统对拓扑信息的分辨力。因此区域内的目标个数、疏密程度与划分的拓扑单元大小有着直接的关联;

3）弥散化系数的确定

弥散化系数是对系统中各种不确定性的表征。雷达系统的性能（如随机误差等）与具体拓扑单元的大小将共同决定弥散化系数的大小，他们之间的最优量化关系式也需要继续研究。

7结束语

本文给出了基于参考目标拓扑矩阵的模糊航迹关联算法实际应用的方法，通过对结果分析得出采用此类模式识別算法，将模糊贴近度作为相似性的度量，使得关联过程更贴近了人脑的工作模式，可获得更好的关联结果。综上所述，该算法具有较好的推广应用价值。

参考文献：

[1] 柴昱.自动化系统中多雷达数据融合子系统的研究与实现[D].成都：电子科技大学，2010.

[2] 杨露菁，余华.多源信息融合理论与应用[M].2版.北京：北京邮电大学出版社，2011：13.

[3] 祁友杰，王琦.多源数据融合算法综述[J].航天电子对抗，2017，33（6）：37-41.

[4] 王成，刘亚峰，王新成，等.分类器的分类性能评价指标[J].电子设计工程，2011，19（8）：13-15，21.

【通联编辑：梁书】

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。