网站首页  词典首页

请输入您要查询的论文：

　

标题 多试飞数据流文件的融合处理
范文 胡汇洋等



摘 要： 为了向型号科研提供一个高质量、高精度的统一时间基准的数据信息，根据型号试飞需求，将来自多个相同或不同类型的数据流文件的参数数据进行融合处理。介绍线形插值、时间逼近及采样保持的数据融合算法，比较分析相关算法不同情况下的有效性，为试飞数据流文件的融合处理提供了依据。
关键词： 数据融合； 线性插值； 时间逼近； 采样保持
中图分类号： TN911?34 文献标识码： A 文章编号： 1004?373X（2015）08?0047?03
Fusion processing of multiple data stream files from flight test
HU Hui?yang， LI Yang， XU Ying?kang
（Chinese Flight Test Establishment， Xian 710089， China）
Abstract： To provide a high?quality and high?precision unified time benchmark data information for research projects， fusion processing of the parameter data from multiple same or different types of data stream files is often required according to the flight test demand. The data fusion algorithm for linear interpolation， time approaching and sample hold is introduced in this article. The effectiveness of relevant algorithms under different circumstances is compared and analyzed. It provided a foundation for fusion processing of flight test data stream files.
Keywords： data fusion； linear interpolation； time approaching； sample hold
0 引 言
随着飞行试验技术的高速发展，对飞行试验数据处理也提出了很高的要求。目前试飞数据的种类越来越多，除了常规的PCM数据以外，各类总线数据、外测数据等都是单独进行测试和处理，这就需要多台采集设备采集和记录数据，造成不同采集设备采集的数据在时间上会有一些差异（也使得各设备采集采样时刻不一致）。但根据一些试飞科目的要求，必须要把同一科目的来自不同采集器的相关参数放在同一个文件中才能对飞机的性能、品质做出准确的判断，也就是要在统一的时间基准上对相关参数进行分析。这就要求必须对多数据流的数据进行融合同步处理[1]，为型号提供一个满足课题要求的统一时间基准[2]的数据信息。
本文就多数据流参数的融合进行初步的探讨，并针对不同情况给出了相应的融合方法。
1 多数据流数据融合前的准备
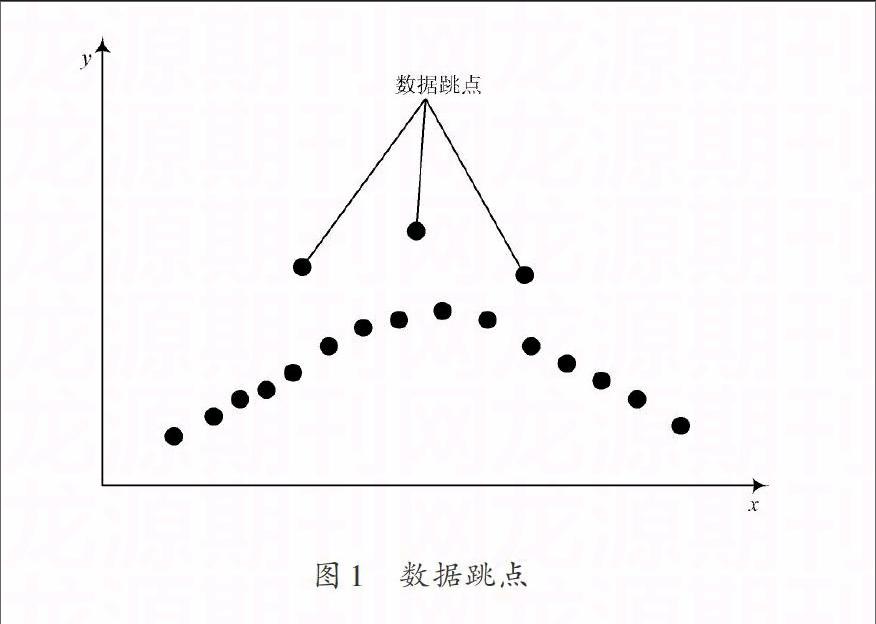
野点剔出[3]是多数据流数据融合处理的一个重要环节。野点也称为跳点，如图1所示，其是指不是被测对象本身正常跳变的记录，而是由于传感器、变换器及传输中的干扰等造成的异常跳点，也即是测量设备及传输等所造成的不正确点。
对于野点分为时间跳点和参数值的跳点，虽然异常值是个别的，但是它对于数据分析的结果影响是比较严重的，能够影响多数据流文件的融合处理效果甚至会导致融合失败。
对于时间跳点来说，由于多数据流的数据融合是多数据流在时间上的协调统一，时间跳点的剔出就显得尤为重要。计算时间t的公式为：[t=h×3 600+m×60+][s+ms1 000]，正常而言（飞行时间不过午夜零点），时间参数应该是一个连续递增的序列，即：[0（1） [tn-1tn+1]，且[tn+1=tn-1+2Δt]；
（2） [tn-1（3） [tn≥24×3 600]。
当然，以上只是单点的时间跳点，还会有多点的情况。
对于参数数据跳点的剔出，目前剔除野值的方法很多[3?4]， 常用的有中点判别法和莱特准则判别法等。 中点判别法是利用正交多项式，按最小二乘原理每5点作一个拟合曲线，计算拟合值与原始值之差，然后对其中点进行判断，条件一般设为按正态分布计算的约80%概率加上一些附加条件，如幅值限制等，对于不符合条件的视其为野值；莱特准则是从概率角度考虑，把剩余误差的绝对值超过3倍的标准差作为条件，如果条件成立则该点为野值点，从而加以剔除。
2 多数据流数据融合
多数据流数据的融合越来越多地被要求作为事后数据处理的一部分，根据课题的要求和参数性质的不同，选择适当的算法对多数据流的数据进行融合处理。不管使用哪种数据融合的算法，数据融合都应在以下前提下进行：
（1） 参与融合数据的采样率要足够反映参数的变化频率，即参数的采样率是合适的[5]。
（2） 低采样率的参数向高采样率的参数融合，反之是没有意义的。
（3） 各个数据流要统一授时。
每个数据流的数据文件都有自己固定的时间序列，数据融合时，选择其中一个数据文件中的时间序列为基准，该文件称为基准文件，其他数据流文件的参数都要统一到这一时间基准上来。


2.1 多数据流数据融合的算法描述
2.1.1 线性插值的算法描述
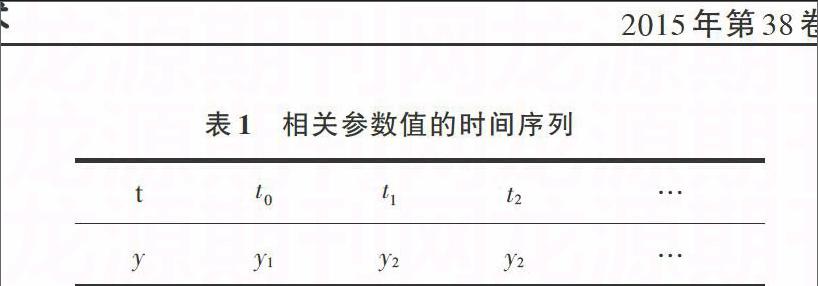
用来描述客观现象的函数[f（x）]通常是比较复杂的，虽然可以肯定这个函数在某个范围内有存在，但很难找到它的具体表达式，在许多场合，需要通过实验或数值计算来揭示这些客观现象。飞行试验也不例外，飞行试验获得了相关参数的在时间序列上的离散点，如表1所示。
这里假设参数变量[y]是时间[t]的函数[y=f（t）]，飞行试验给出了该函数的离散采样点，如何求出时间区间[[tk]，[tk+1]]（[tk≠tk+1]，[k=0，1，2，…，n]）中某一时间[t]的函数值，这就需要用到插值的方法。插值的基本思想是，设法构造某个多项式函数[y=p（x）]作为[f（x）]的近似表达式，然后计算[y=p（t）]的值作为[f（t）]近似值。
线性插值是最常见的插值方法[6?7]，对于缓变的模拟量参数，在采样率比较高的情况下，任意相邻两点之间的曲线可以用直线去逼近，并且采样率越高，逼近精度越高。其插值的表达式为：
[y=yk+（t-tk）·（yk+1-yk）（tk+1-tk）]
2.1.2 基于时间逼近的多数据流数据融合算法
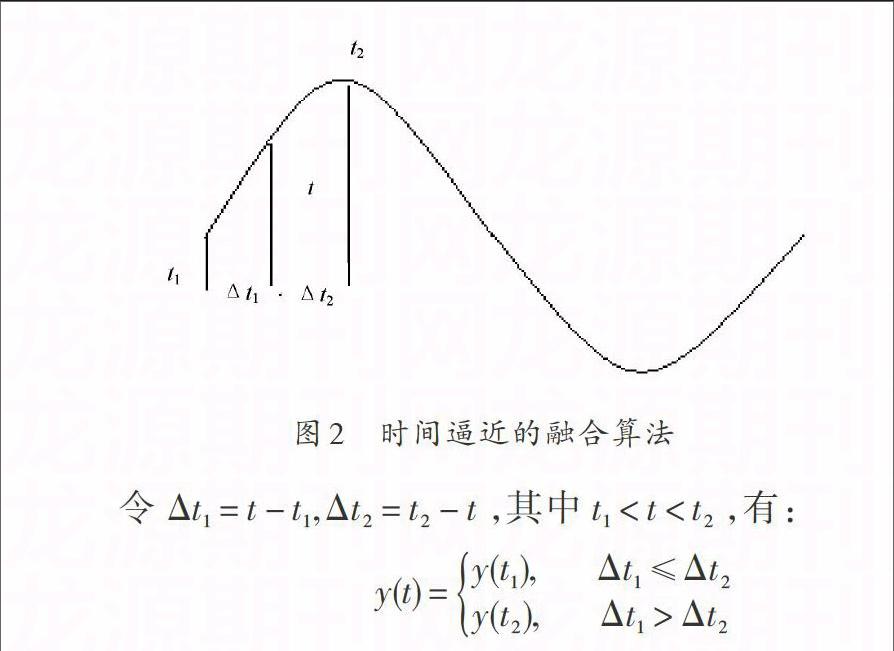
线形插值的方法是在原有采样点的基础上经计算产生某一时刻t的参数值，而时间逼近的数据融合思想是[8?9]：选择基准时刻t左右相邻两点的时刻[t1，t2]，以距离t时刻最近的时刻的参数值作为该时刻t的参数值，以保持原始采样值不变，如图2所示。
令[Δt1=t-t1，Δt2=t2-t]，其中[t1[y（t）=y（t1）， Δt1≤Δt2y（t2）， Δt1>Δt2]
2.1.3 基于采样保持的数据融合
在数据处理时，除了模拟量外，还会有大量的离散量和开关量，它们表示了飞机某些功能的状态，对离散量和开关量来说，如果使用插值的方法，会出现小数，对于小数是不符合参数定义的，也无法给出一个合理的解释。所以对于这些变量的处理采取采样保持的方法，即当要判断某一参数当前时刻的状态时，而记录设备又没有记录当前的数据，就用上一时刻的状态代替当前时刻的状态。这是合理的，因为在没有获得下一个采样点的信息之前，就认为当前状态是上一个状态的延续和保持，这符合人的逻辑思维。
2.2 数据融合的实例分析
下面以某实验仿真的多流数据融合为例，分别说明基于线形插值和基于时间逼近的多流数据融合的方法，这里只讨论两个数据流的融合，多于两个数据流的融合类似。图3为数据融合前的数据曲线，图4为数据融合后的数据曲线。对比融合前后的数据图可知，数据融合前后的数据基本一致，特别是参数的特征数据（峰/谷值）比较一致，达到了一定精度的要求。

图3 数据融合前的曲线

图4 数据融合后的曲线
这里试图利用线形插值的方法对跳变参数进行数据融合，以某实验仿真的颤振数据为例，图5，图6分别为某一颤振参数数据融合前后的数据曲线图，从图中可以看出该参数经过线形插值后，其参数幅值发生了明显的衰减，这就明显改变了参数的特性，显然是不符合课题要求的。

图5 颤振参数数据融合前的曲线
为了保持参数的幅值特性不发生变化，这里采用了基于时间逼近的数据融合方法对上述数据进行融合处理，处理后的数据如图7所示。从图5、图7对比可看到，基于时间逼近的方法较好地保持了原数据的幅值特性。

图6 颤振参数数据融合后的曲线

图7 基于时间逼近的颤振参数融合后数据曲线
3 结 语
本文讨论了多数据流的融合问题，主要用到线形插值算法和基于时间逼近的方法。对数字量和开关量，采用的是采样保持的方法，并以实例分析了线形插值算法和基于时间逼近的方法在多数据流文件融合中的应用。最后发现每一种算法都不是完美的，线形插值的方法虽然保证了参数之间的时间相关性，但是插值本身就具有平滑的作用，对参数的幅值有一定的影响。基于时间逼近的方法虽然对参数的幅值影响较小，但是该方法本身是将参数做了时间轴上的平移，改变了参数的相位，影响了参数之间的时间相关性。对于模拟量的缓变参数，采样率足够，并且对参数的时间相关性要求较高的情况下采用线形插值的数据融合方法；对于跳变的参数，在数据融合后更关注参数的幅值特性，在参数的时间相关性要求不高的情况下采用时间逼近的数据融合方法。
参考文献
[1] 杨华，林卉.数据融合的研究综述[J].矿山测量，2005（3）：24?27.
[2] 刘钊，戴斌.多传感器信息融合中时间同步方法的研究[J].计算机仿真，2009，26（6）：124?127.
[3] 徐利娜，陈俊彪.靶场外弹道数据处理中的实时野值剔除算法[J].应用光学，2012，33（1）：90?95.
[4] 赖素建，靳晓雄.信号预处理中错点剔除方法的研究[J].佳木斯大学学报，2011，29（3）：333?335.
[5] 徐伟宗.采样频率对行波测距影响的仿真分析[J].电力系统及其自动化学报，2014，26（4）：76?80.
[6] 冯慧君，陶素娟，李隆.基于双线性插值的图像放缩技术与实现[J].计算机应用与软件，2004，21（7）：117?119.
[7] 梁小利，孙洪淋.基于线性插值算法的图像缩放及实现[J].长沙通信职业技术学院学报，2008，7（2）：49?51.
[8] 彭芳瑜，周云飞，周济.基于插值与逼近的复杂曲面拟合[J].工程图学学报，2002，23（4）：87?96.
[9] 聂志峰，周慎杰.基于C1自然邻近插值的曲面拟合[J].工程图学学报，2010，31（1）：110?115.
[10] 何渝.计算机常用数值算法与程序（C++版）[M].北京：人民邮电出版社，2003.





技术文
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2024/12/23 9:38:16