一道实验型试题的赏析、探源及其对教学的启示
张安军
【摘要】2017年台州市中考数学试题命制一道实验型压轴题,本题背景新颖,梯度合理;凸显核心素养,凸显能力考查.对试题进行探源,用几何的方法求一元二次方程的根,古希腊数学家欧几里得、阿拉伯数学家花拉子密、中国古代数学家赵爽给出了不同的解法.注重实验操作背后质疑和求证,培养理性思维;重视实验过程中活动经验的积累,提升数学思想方法.
【关键词】实验型试题;特色欣赏;试题探源;课堂教学
《义务教育数学课程标准(2011年版)》指出:“学生学习应当是一个生动活泼的、主动的和富有个性的过程.认真听讲、积极思考、动手实践、自主探索、合作交流等,都是学习数学的重要方式.学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程.”为了贯彻课程标准的理念,检测理念的落实情况,正确引导日常的教学,发挥中考应有教学导向功能.2017年浙江省台州市中考数学试题的第24题(压轴题)命制一道实验型试题,本题既具有实验型试题所特有的实验探索的特点,又具有探究型试题所侧重的“能力探究”的立意特色.本题要求学生在阅读理解的基础上,让学生经历实验操作、计算、推理、验证,借助于实验,探究并解决问题,实质上是将课题学习、数学活动过程、数学思考等考察目标融入其中[1].侧重“做数学”和“数学化”过程与能力的考察,本试题在“创设问题情境、内涵丰富、侧重理性思维、注重过程与方法渗透”这方面做了有益的尝试和探索,试题引起的反响也给我们留下了许多有益的思考.
1试题呈现及简述
题目(原试题中的第24题)在平面直角坐标系中,借助直角三角板可以找到一元二次方程的实数根.比如对于方程x2-5x+2=0,操作步骤是:
第一步:根据方程的系数特征,确定一对固定点A(0,1),B(5,2);
第二步:坐标平面中移动一个直角三角板,使一条直角边恒过点A,另一条直角边恒过点B;
第三步:在移动过程中,当三角板的直角顶点落在x轴上点C处时,点C的横坐标m即为该方程的一个实数根(如图1);
第四步:调整三角板直角顶点的位置,当它落在x轴上另一点D处时,点D的横坐标n即为该方程的另一个实数根.

(2)结合图1,请证明“第三步”操作得到的m就是方程x2-5x+2=0的一个实数根;
(3)上述操作的关键是确定两个固定点的位置.若要以此方法找到一元二次方程ax2+bx+c=0(a≠0,b2-4ac≥0)的实数根,请你直接写出一对固定点的坐标;
(4)实际上,(3)中的固定点有无数对.一般地,当m1,n1,m2,n2与a,b,c之间应该满足怎样的关系时,点P(m1,n1),Q(m2,n2)就是符合要求的一对固定点?
上述文字虽400多字,由于本阅读不涉及数学概念的理解,仅是一个说明性的实验操作,实验操作结合具体的方程,叙述清楚,操作明确,学生在问题的理解上明白、易懂.从问题的设置上看,起点低,巧用题组关系,层层递进,借助直角三角板利用直角坐标系和特殊的固定点求解一元二次方程的根.用实验操作的方法求解一元二次方程,构思新颖、独特.本题整合了相似三角形、一元二次方程、勾股定理等初中核心知识,使得各类知识在此题中交汇呼应,浑然天成,丝毫不显知识堆砌的痕迹.
2特色赏析
2.1背景新颖,梯度合理
学生求解一元二次方程,常用的方法是用公式法、因式分解法和配方法,然而本题求解一元二次方程却另辟蹊径,用三角板在直角坐标系中也能求解,从学生的最近发展区中创设有助于学生自主学习的问题情境,从而激发学生求知的欲望.阅读材料的内容命题者精心组织,用初中常用的数学概念(如“一元二次方程、实数根、方程的系数、平面直角坐标系、点的坐标、直角顶点、恒过点等”)介绍求解一元二次方程的新方法.第(1)小问通过阅读,按照“第四步”的操作方法求作方程的另一根,考查学生数学阅读对信息获取的能力;第(2)小问对这一操作进行理性的追问,这样的操作所得到点的横坐标为什么就是一元二次方程的根呢?让学生经历从感性到理性,从质疑到验证,思维经历了从具体的操作到理性的思辨;由于上述的操作是基于具体的一元二次方程,第(3)小问很自然引导学生对于一般的一元二次方程操作时固定点有多少对?这样的固定点唯一吗?固定点的坐标和一元二次方程中的系数之间的数量进行探究,思维从具体向一般化发展;第(4)小问是从(3)小问的反面去思考,探索两个固定点的坐标和一元二次方程的系数之间有怎样的关系,整个问题设计从简单到复杂,从具体到开放,设计了相互关联的问题,层次非常分明,难度逐级递进,不同层次的学生都有不同的收获,犹如爬山欣赏风景,不同的高度,展现不同的美景;会当临绝顶,一览众山小,那是数学高峰的诱惑.这样设计既是对学生的探究能力、创新能力的一次检验,又是能力立意的充分体现,有效地抑制题海战术,减轻学生课业负担,对我们的教学有积极的引导作用.
2.2凸显核心素养,在交会之处做文章
中考数学压轴题须突出数学的本质,紧扣核心知识,在核心知识的交会处设计试题,此题考查的内容都是初中数学中的一些核心内容.从知识层面看,主要考查了平面直角坐标系,一元二次方程、相似三角形、勾股定理等知识,这些知识都是初中的核心知识,从方法层面看,例如第(2)小问把上述第(1)小问中的数转化成形,构建两个直角三角形相似,通过相似比构建方程,对比方程的系数,验证x轴上所求作点的横坐标就是一元二次方程的根,蕴含数形结合,方程思想;第(3)小问思维从特殊拓展到一般,在一般化下的一元二次方程,如何寻找ax2+bx+c=0的固定点,借助阅读材料中具体的方程x2-5x+2=0,首先把ax2+bx+c=0系数变成1,即x2+bax+ca=0,化归到阅读材料中的固定点问题,可以从特殊值思考,假定其中一个固定点A(0,1),通过相似计算另一固定点B(-ba,ca),也可以从一般化层面思考,假定其中一个固定点A(0,t)(t≠0的参数),通过计算得到另一固定点B(-ba,cat)(t≠0的参数),试题中所蕴含的思想从特殊到一般,转化思想;第(4)小问存在点P(m1,n1),Q(m2,n2),探究这两点坐标和一元二次方程ax2+bx+c=0系数之间的关系,利用相似三角形或者勾股定理等把它转化到刚解决过的问题,所蕴含转化思想、方程思想、数形结合思想等.从经验层面看,解决此题需要学生具有一定的基本活动经验,例如阅读材料中具体方程如何操作,如何确定固定点,为一般化方程积累操作活动经验,并进行推广和提升,因此,在平时的教学中,要注重学生基本活动经验的积累,让学生经历知识的发现与提出过程,发生与发展过程,探索与应用过程,方法与规律的概括过程,引导学生进行反思与评价,使学生在一点一滴活动经验积累的基础上,完成对知识的建构,实现对基础知识、基本技能和基本方法的內化,有效提升学生的学习能力.
2.3方法多元,各显神通考能力
学业考试应体现《义务教育数学课程标准(2011年版)》所倡导“应建立目标多元、方法多样的评价体系.”

第(3)小题结论开放,方法多样,先把方程ax2+bx+c=0(a≠0)可化为x2+bax+ca=0.
模仿研究小组作法可得:A(0,1),B(-ba,ca)或A(0,1a),B(-ba,c).当点A在y轴上时,形如A(0,t),B(-ba,cat)(t≠0)即可.
第(4)小题解法:

m1,m2,n1,n2与a,b,c满足的关系为:
m1+m2=-ba,①
m1m2+n1n2=ca.②
①②式的推导过程如下:
设方程ax2+bx+c=0的根为x0.
(ⅰ)n1,n2均不为零时,根据三角形相似可得:|n1||m1-x0|=|m2-x0||n2|.
当n1,n2符号为同号时,点P,Q分别在AE,BF上,m1-x0,m2-x0的符号必为异号;当n1,n2符号为异号时,点P,Q分别在EF,AB上,m1-x0,m2-x0的符号必为同号.
综上可得:n1n2=-(m1-x0)(m2-x0),化简可得:x20-(m1+m2)x0+m1m2+n1n2=0,通过比较系数可得①②两个式子.
(ⅱ)n1,n2至少有一个为零时,①②两个式子仍然成立.
解法二:点P(m1,n1),Q(m2,n2),设方程ax2+bx+c=0的根为x0.利用勾股定理可得:(m1-x0)2+n21+(m2-x0)2+n22=(m1-m2)2+(n1-n2)2.
上式化简得:x20-(m1+m2)x0+m1m2+n1n2=0,通过比较系数可得①②两个式子.

设方程的根为x,根据三角形相似可得x2-(m1+m2)x+m1m2+n1n2=0,又因为ax2+bx+c=0,即x2+bax+ca=0.
比较系数可得
m1+m2=-ba,①
m1m2+n1n2=ca.②
解法四:因为m1+m22=-b2a,所以
m1+m2=-ba,①
根据三角形相似可得
m1m2+n1n2=ca.②
3试题探源
事实上用几何的方法求作一元二次方程的根,早在公元前古希腊数学家欧几里得就给出几何求法,《几何原本》卷二命题11给出了等价于求一元二次方程正实根的方法,如图5,PB是⊙O1的直径,PA=c,AB=1,AE⊥PB于A点,则可算得AE=c,⊙O2的圆心在PB的延长线上,直径是b,四边形AEFD是矩形,由FD2=CD×DQ,则x1=CD,x2=DQ是一元二次方程x2-bx=c的两个根;图6中,FC2=FM×FN,则x1=FM,x2=FN是一元二次方程x2+bx=c的两个根;图5图6上述中考试题,也可以看成如图7所示,在平面直角坐标系中,⊙O是以(0,1)和(-b,c)为直径,若⊙O与x轴有两个交点,这两个交点的横坐标x1,x2就是方程x2+bx+c=0的根.
然而北师大版《九年级义务数学教科书(上册)》52页“读一读”中以“x2+2x-35=0”为例介绍两种几何作图法,一种是中国古代数学家赵爽的解法,如图8所示,正方形ABCD是由4个相同的矩形和一个正方形EFGH组成,矩形的长比宽大2,正方形EFGH的边长是2,由大正方形ABCD面积等于4个矩形的面积和一个小正方形EFGH面积之和,设矩形的宽为x,可得(x+2+x)2=4×35+22,因此解得一个正根为x=5;公元8世纪阿拉伯数学家花拉子密也给出几何解法,如果用花拉子密的方法,如图9所示,正方形ABCD是由正方形EFCH和两个全等的矩形(矩形ABFN和矩形AMHD)组成,其中矩形ABFN和矩形AMHD重叠部分为正方形,正方形AMEN的边长为1,设HC=x,可得(x+1)2=35+1,解得其中一个正根为x=5;当然几何作图的方法可以推广得一般形式:ax2+bx=c.
赵爽的方法和花拉子密的方法虽然构造几何图形不同,但本质上都是相同,构造大正方形,然而花拉子米的解法更直观地体现了配方法的几何意义.
4教学启示
2017年台州市考生大约60564人,数学试卷总分150分,本题压轴题共14分,考生各小题得分如下表:
第24题第(1)问第(2)问第(3)问第(4)问分值143434平均得分35920112043004难度系数026067028014001从表中可以看出,除第(1)小问外,其余3个小问,难度系数都比较低,这反应出一线教师在课堂教学中存在着一定的问题,也给实验教学以启发.
4.1注重实验操作背后质疑和求证,培养理性思维
图10第(2)小问对上述阅读材料进行追问,要求学生对这一操作的正确性进行验证,数学实验不仅要会“直观的做”,而且还会“抽象的思”.从这次学生答题来看,第(1)小问,大部分学生能读懂题意并能操作,第(2)小问学生虽能构造出“一线三直角”,但大部分学生未能理解所构造相似三角形和一元二次方程之间的关系,思维层面不能进行深层次理解和思考,也反映出平常实验教学中虽有直观操作、观察、比较、归纳和合情推理,但缺乏严谨性的求证,实验教学更需要运用数学的思维方式检验或反思数学结论的能力,培养学生严谨的思维和理性精神.例如在一次函数图象性质的教学中,为了让学生理解一次函数的图象是一条直线,如图10所示,大部分老师会利用几何画板迭代或者轨迹功能进行演示实验,点与点之间慢慢地从疏朗变到稠密,让学生形象地观察到一次函数的图象是一条直线.对这一过程的演示老师能否引导学生深层次地思考呢,能否引导学生用质疑、批判的眼光审视这一问题呢?图11为什么这些点都是在一条直线上呢?引导运用数学的思维方式检验或反思数学结论,如图11所示,能否证明相邻A,B,C三点共线吗?运用全等三角形证明这一結论,培养学生思维的深刻性和严谨性.
4.2重視实验过程中活动经验的积累,提升数学思想方法
第(3)小问寻找固定点,首先化“ax2+bx+c=0”系数为1的“x2+bax+ca=0”,这样转化到阅读材料中特殊方程中如何寻找固定点,体现数学中的转化思想;第(4)小问从第(3)小问反面思考,如果已知两固定点,探究两固定点的坐标与a,b,c之间的关系.此题揭示实验操作探究问题的一般过程:动手操作、思考发现、质疑求证、实践探究、类比拓展,渗透了学习数学的一般方法:从特殊到一般、类比与归纳、联想与拓展、转化思想等,让学生经历数学问题的提出、研究、解决、拓展的全过程,在这次考试学生实际答题中,只有极小部分学生能够深层次探究,也反映出日常课堂教学中虽有实验操作探究的活动,但没有实验过程中操作的反思,没有对重复活动经验中提升和概括.例如,北师大版《九年级义务数学教科书(上册)》52页“读一读”中以“x2+2x-35=0”为例介绍两种几何作图法,如果我们的老师仅这个例子进行讲解,让学生进行模仿性地操作,这样的教学谈不上活动经验的积累和思想方法的提升,相反挖掘阅读材料的内容,进行如下设计:
问题1:三国时期数学家赵爽和阿拉伯数学家花拉子密都用形的方法探讨了一元二次方程的解法,例如,一元二次方程“x2+2x=35”两个数学家给出如图8、9所示的解法.请你利用这两个图求解方程:“x2+2x-35=0”.
问题2:请你用赵爽(花拉子密)构图的方法解方程“x2-4x=5”;
问题3:请你用赵爽(花拉子密)构图的方法解方程“2x2+3x=5”;
问题4:请你用赵爽(花拉子密)构图的方法解方程“x2+bx=c”;
问题5:请你用赵爽(花拉子密)构图的方法解方程“ax2+bx=c”.
上述问题2是问题1的变式,从模仿到迁移;问题3是问题2的拓展和提升,首先把“2x2+3x=5”的化系数为1,即“x2+15x=25”,这样问题3转化为问题1;问题4是问题3的一般化;问题5又是问题4的一般化.上述问题设计中,学生在重复构造正方形解一元二次方程,思维经历了从模糊到朦胧,从朦胧到清晰,学生构图的过程就是从无意识模仿地画图到有点方法地构图,从有点方法构图到自己创造性地构图,每次的构图都不仅是上一次地重复,而是上一次构图的拓展和提升,这样在重复操作构图解决一元二次方程中,教师引导学生进行反思总结,在不同问题中用了哪些相同的操作方法,在总结中不断优化学生的思维,提升学生数学思想方法.
参考文献
[1]吕小保.新课改背景下的操作探究型试题及教学启示,[J].数学通报,2008(10):59-61.
【摘要】2017年台州市中考数学试题命制一道实验型压轴题,本题背景新颖,梯度合理;凸显核心素养,凸显能力考查.对试题进行探源,用几何的方法求一元二次方程的根,古希腊数学家欧几里得、阿拉伯数学家花拉子密、中国古代数学家赵爽给出了不同的解法.注重实验操作背后质疑和求证,培养理性思维;重视实验过程中活动经验的积累,提升数学思想方法.
【关键词】实验型试题;特色欣赏;试题探源;课堂教学
《义务教育数学课程标准(2011年版)》指出:“学生学习应当是一个生动活泼的、主动的和富有个性的过程.认真听讲、积极思考、动手实践、自主探索、合作交流等,都是学习数学的重要方式.学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程.”为了贯彻课程标准的理念,检测理念的落实情况,正确引导日常的教学,发挥中考应有教学导向功能.2017年浙江省台州市中考数学试题的第24题(压轴题)命制一道实验型试题,本题既具有实验型试题所特有的实验探索的特点,又具有探究型试题所侧重的“能力探究”的立意特色.本题要求学生在阅读理解的基础上,让学生经历实验操作、计算、推理、验证,借助于实验,探究并解决问题,实质上是将课题学习、数学活动过程、数学思考等考察目标融入其中[1].侧重“做数学”和“数学化”过程与能力的考察,本试题在“创设问题情境、内涵丰富、侧重理性思维、注重过程与方法渗透”这方面做了有益的尝试和探索,试题引起的反响也给我们留下了许多有益的思考.
1试题呈现及简述
题目(原试题中的第24题)在平面直角坐标系中,借助直角三角板可以找到一元二次方程的实数根.比如对于方程x2-5x+2=0,操作步骤是:
第一步:根据方程的系数特征,确定一对固定点A(0,1),B(5,2);
第二步:坐标平面中移动一个直角三角板,使一条直角边恒过点A,另一条直角边恒过点B;
第三步:在移动过程中,当三角板的直角顶点落在x轴上点C处时,点C的横坐标m即为该方程的一个实数根(如图1);
第四步:调整三角板直角顶点的位置,当它落在x轴上另一点D处时,点D的横坐标n即为该方程的另一个实数根.

(2)结合图1,请证明“第三步”操作得到的m就是方程x2-5x+2=0的一个实数根;
(3)上述操作的关键是确定两个固定点的位置.若要以此方法找到一元二次方程ax2+bx+c=0(a≠0,b2-4ac≥0)的实数根,请你直接写出一对固定点的坐标;
(4)实际上,(3)中的固定点有无数对.一般地,当m1,n1,m2,n2与a,b,c之间应该满足怎样的关系时,点P(m1,n1),Q(m2,n2)就是符合要求的一对固定点?
上述文字虽400多字,由于本阅读不涉及数学概念的理解,仅是一个说明性的实验操作,实验操作结合具体的方程,叙述清楚,操作明确,学生在问题的理解上明白、易懂.从问题的设置上看,起点低,巧用题组关系,层层递进,借助直角三角板利用直角坐标系和特殊的固定点求解一元二次方程的根.用实验操作的方法求解一元二次方程,构思新颖、独特.本题整合了相似三角形、一元二次方程、勾股定理等初中核心知识,使得各类知识在此题中交汇呼应,浑然天成,丝毫不显知识堆砌的痕迹.
2特色赏析
2.1背景新颖,梯度合理
学生求解一元二次方程,常用的方法是用公式法、因式分解法和配方法,然而本题求解一元二次方程却另辟蹊径,用三角板在直角坐标系中也能求解,从学生的最近发展区中创设有助于学生自主学习的问题情境,从而激发学生求知的欲望.阅读材料的内容命题者精心组织,用初中常用的数学概念(如“一元二次方程、实数根、方程的系数、平面直角坐标系、点的坐标、直角顶点、恒过点等”)介绍求解一元二次方程的新方法.第(1)小问通过阅读,按照“第四步”的操作方法求作方程的另一根,考查学生数学阅读对信息获取的能力;第(2)小问对这一操作进行理性的追问,这样的操作所得到点的横坐标为什么就是一元二次方程的根呢?让学生经历从感性到理性,从质疑到验证,思维经历了从具体的操作到理性的思辨;由于上述的操作是基于具体的一元二次方程,第(3)小问很自然引导学生对于一般的一元二次方程操作时固定点有多少对?这样的固定点唯一吗?固定点的坐标和一元二次方程中的系数之间的数量进行探究,思维从具体向一般化发展;第(4)小问是从(3)小问的反面去思考,探索两个固定点的坐标和一元二次方程的系数之间有怎样的关系,整个问题设计从简单到复杂,从具体到开放,设计了相互关联的问题,层次非常分明,难度逐级递进,不同层次的学生都有不同的收获,犹如爬山欣赏风景,不同的高度,展现不同的美景;会当临绝顶,一览众山小,那是数学高峰的诱惑.这样设计既是对学生的探究能力、创新能力的一次检验,又是能力立意的充分体现,有效地抑制题海战术,减轻学生课业负担,对我们的教学有积极的引导作用.
2.2凸显核心素养,在交会之处做文章
中考数学压轴题须突出数学的本质,紧扣核心知识,在核心知识的交会处设计试题,此题考查的内容都是初中数学中的一些核心内容.从知识层面看,主要考查了平面直角坐标系,一元二次方程、相似三角形、勾股定理等知识,这些知识都是初中的核心知识,从方法层面看,例如第(2)小问把上述第(1)小问中的数转化成形,构建两个直角三角形相似,通过相似比构建方程,对比方程的系数,验证x轴上所求作点的横坐标就是一元二次方程的根,蕴含数形结合,方程思想;第(3)小问思维从特殊拓展到一般,在一般化下的一元二次方程,如何寻找ax2+bx+c=0的固定点,借助阅读材料中具体的方程x2-5x+2=0,首先把ax2+bx+c=0系数变成1,即x2+bax+ca=0,化归到阅读材料中的固定点问题,可以从特殊值思考,假定其中一个固定点A(0,1),通过相似计算另一固定点B(-ba,ca),也可以从一般化层面思考,假定其中一个固定点A(0,t)(t≠0的参数),通过计算得到另一固定点B(-ba,cat)(t≠0的参数),试题中所蕴含的思想从特殊到一般,转化思想;第(4)小问存在点P(m1,n1),Q(m2,n2),探究这两点坐标和一元二次方程ax2+bx+c=0系数之间的关系,利用相似三角形或者勾股定理等把它转化到刚解决过的问题,所蕴含转化思想、方程思想、数形结合思想等.从经验层面看,解决此题需要学生具有一定的基本活动经验,例如阅读材料中具体方程如何操作,如何确定固定点,为一般化方程积累操作活动经验,并进行推广和提升,因此,在平时的教学中,要注重学生基本活动经验的积累,让学生经历知识的发现与提出过程,发生与发展过程,探索与应用过程,方法与规律的概括过程,引导学生进行反思与评价,使学生在一点一滴活动经验积累的基础上,完成对知识的建构,实现对基础知识、基本技能和基本方法的內化,有效提升学生的学习能力.
2.3方法多元,各显神通考能力
学业考试应体现《义务教育数学课程标准(2011年版)》所倡导“应建立目标多元、方法多样的评价体系.”

第(3)小题结论开放,方法多样,先把方程ax2+bx+c=0(a≠0)可化为x2+bax+ca=0.
模仿研究小组作法可得:A(0,1),B(-ba,ca)或A(0,1a),B(-ba,c).当点A在y轴上时,形如A(0,t),B(-ba,cat)(t≠0)即可.
第(4)小题解法:

m1,m2,n1,n2与a,b,c满足的关系为:
m1+m2=-ba,①
m1m2+n1n2=ca.②
①②式的推导过程如下:
设方程ax2+bx+c=0的根为x0.
(ⅰ)n1,n2均不为零时,根据三角形相似可得:|n1||m1-x0|=|m2-x0||n2|.
当n1,n2符号为同号时,点P,Q分别在AE,BF上,m1-x0,m2-x0的符号必为异号;当n1,n2符号为异号时,点P,Q分别在EF,AB上,m1-x0,m2-x0的符号必为同号.
综上可得:n1n2=-(m1-x0)(m2-x0),化简可得:x20-(m1+m2)x0+m1m2+n1n2=0,通过比较系数可得①②两个式子.
(ⅱ)n1,n2至少有一个为零时,①②两个式子仍然成立.
解法二:点P(m1,n1),Q(m2,n2),设方程ax2+bx+c=0的根为x0.利用勾股定理可得:(m1-x0)2+n21+(m2-x0)2+n22=(m1-m2)2+(n1-n2)2.
上式化简得:x20-(m1+m2)x0+m1m2+n1n2=0,通过比较系数可得①②两个式子.

设方程的根为x,根据三角形相似可得x2-(m1+m2)x+m1m2+n1n2=0,又因为ax2+bx+c=0,即x2+bax+ca=0.
比较系数可得
m1+m2=-ba,①
m1m2+n1n2=ca.②
解法四:因为m1+m22=-b2a,所以
m1+m2=-ba,①
根据三角形相似可得
m1m2+n1n2=ca.②
3试题探源
事实上用几何的方法求作一元二次方程的根,早在公元前古希腊数学家欧几里得就给出几何求法,《几何原本》卷二命题11给出了等价于求一元二次方程正实根的方法,如图5,PB是⊙O1的直径,PA=c,AB=1,AE⊥PB于A点,则可算得AE=c,⊙O2的圆心在PB的延长线上,直径是b,四边形AEFD是矩形,由FD2=CD×DQ,则x1=CD,x2=DQ是一元二次方程x2-bx=c的两个根;图6中,FC2=FM×FN,则x1=FM,x2=FN是一元二次方程x2+bx=c的两个根;图5图6上述中考试题,也可以看成如图7所示,在平面直角坐标系中,⊙O是以(0,1)和(-b,c)为直径,若⊙O与x轴有两个交点,这两个交点的横坐标x1,x2就是方程x2+bx+c=0的根.

然而北师大版《九年级义务数学教科书(上册)》52页“读一读”中以“x2+2x-35=0”为例介绍两种几何作图法,一种是中国古代数学家赵爽的解法,如图8所示,正方形ABCD是由4个相同的矩形和一个正方形EFGH组成,矩形的长比宽大2,正方形EFGH的边长是2,由大正方形ABCD面积等于4个矩形的面积和一个小正方形EFGH面积之和,设矩形的宽为x,可得(x+2+x)2=4×35+22,因此解得一个正根为x=5;公元8世纪阿拉伯数学家花拉子密也给出几何解法,如果用花拉子密的方法,如图9所示,正方形ABCD是由正方形EFCH和两个全等的矩形(矩形ABFN和矩形AMHD)组成,其中矩形ABFN和矩形AMHD重叠部分为正方形,正方形AMEN的边长为1,设HC=x,可得(x+1)2=35+1,解得其中一个正根为x=5;当然几何作图的方法可以推广得一般形式:ax2+bx=c.
赵爽的方法和花拉子密的方法虽然构造几何图形不同,但本质上都是相同,构造大正方形,然而花拉子米的解法更直观地体现了配方法的几何意义.
4教学启示
2017年台州市考生大约60564人,数学试卷总分150分,本题压轴题共14分,考生各小题得分如下表:
第24题第(1)问第(2)问第(3)问第(4)问分值143434平均得分35920112043004难度系数026067028014001从表中可以看出,除第(1)小问外,其余3个小问,难度系数都比较低,这反应出一线教师在课堂教学中存在着一定的问题,也给实验教学以启发.
4.1注重实验操作背后质疑和求证,培养理性思维
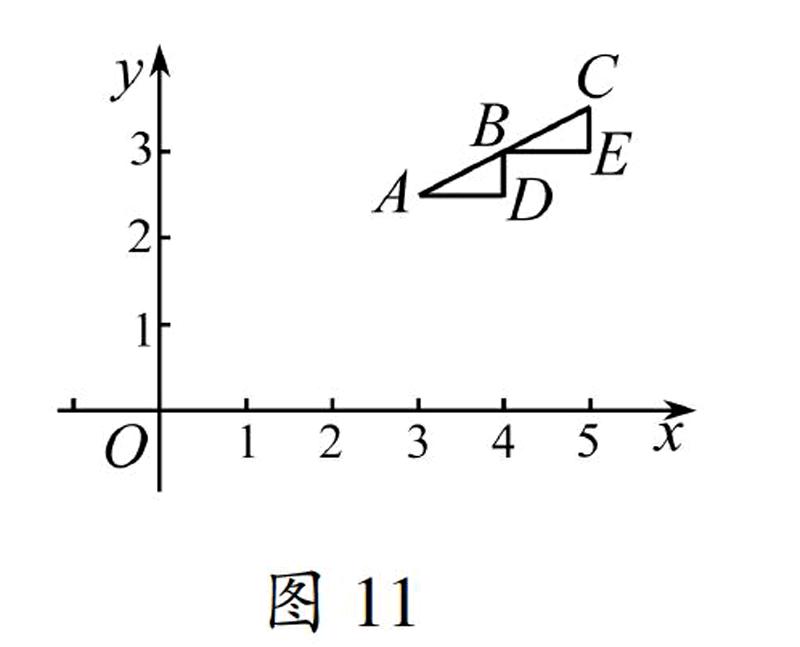
图10第(2)小问对上述阅读材料进行追问,要求学生对这一操作的正确性进行验证,数学实验不仅要会“直观的做”,而且还会“抽象的思”.从这次学生答题来看,第(1)小问,大部分学生能读懂题意并能操作,第(2)小问学生虽能构造出“一线三直角”,但大部分学生未能理解所构造相似三角形和一元二次方程之间的关系,思维层面不能进行深层次理解和思考,也反映出平常实验教学中虽有直观操作、观察、比较、归纳和合情推理,但缺乏严谨性的求证,实验教学更需要运用数学的思维方式检验或反思数学结论的能力,培养学生严谨的思维和理性精神.例如在一次函数图象性质的教学中,为了让学生理解一次函数的图象是一条直线,如图10所示,大部分老师会利用几何画板迭代或者轨迹功能进行演示实验,点与点之间慢慢地从疏朗变到稠密,让学生形象地观察到一次函数的图象是一条直线.对这一过程的演示老师能否引导学生深层次地思考呢,能否引导学生用质疑、批判的眼光审视这一问题呢?图11为什么这些点都是在一条直线上呢?引导运用数学的思维方式检验或反思数学结论,如图11所示,能否证明相邻A,B,C三点共线吗?运用全等三角形证明这一結论,培养学生思维的深刻性和严谨性.
4.2重視实验过程中活动经验的积累,提升数学思想方法
第(3)小问寻找固定点,首先化“ax2+bx+c=0”系数为1的“x2+bax+ca=0”,这样转化到阅读材料中特殊方程中如何寻找固定点,体现数学中的转化思想;第(4)小问从第(3)小问反面思考,如果已知两固定点,探究两固定点的坐标与a,b,c之间的关系.此题揭示实验操作探究问题的一般过程:动手操作、思考发现、质疑求证、实践探究、类比拓展,渗透了学习数学的一般方法:从特殊到一般、类比与归纳、联想与拓展、转化思想等,让学生经历数学问题的提出、研究、解决、拓展的全过程,在这次考试学生实际答题中,只有极小部分学生能够深层次探究,也反映出日常课堂教学中虽有实验操作探究的活动,但没有实验过程中操作的反思,没有对重复活动经验中提升和概括.例如,北师大版《九年级义务数学教科书(上册)》52页“读一读”中以“x2+2x-35=0”为例介绍两种几何作图法,如果我们的老师仅这个例子进行讲解,让学生进行模仿性地操作,这样的教学谈不上活动经验的积累和思想方法的提升,相反挖掘阅读材料的内容,进行如下设计:
问题1:三国时期数学家赵爽和阿拉伯数学家花拉子密都用形的方法探讨了一元二次方程的解法,例如,一元二次方程“x2+2x=35”两个数学家给出如图8、9所示的解法.请你利用这两个图求解方程:“x2+2x-35=0”.
问题2:请你用赵爽(花拉子密)构图的方法解方程“x2-4x=5”;
问题3:请你用赵爽(花拉子密)构图的方法解方程“2x2+3x=5”;
问题4:请你用赵爽(花拉子密)构图的方法解方程“x2+bx=c”;
问题5:请你用赵爽(花拉子密)构图的方法解方程“ax2+bx=c”.
上述问题2是问题1的变式,从模仿到迁移;问题3是问题2的拓展和提升,首先把“2x2+3x=5”的化系数为1,即“x2+15x=25”,这样问题3转化为问题1;问题4是问题3的一般化;问题5又是问题4的一般化.上述问题设计中,学生在重复构造正方形解一元二次方程,思维经历了从模糊到朦胧,从朦胧到清晰,学生构图的过程就是从无意识模仿地画图到有点方法地构图,从有点方法构图到自己创造性地构图,每次的构图都不仅是上一次地重复,而是上一次构图的拓展和提升,这样在重复操作构图解决一元二次方程中,教师引导学生进行反思总结,在不同问题中用了哪些相同的操作方法,在总结中不断优化学生的思维,提升学生数学思想方法.
参考文献
[1]吕小保.新课改背景下的操作探究型试题及教学启示,[J].数学通报,2008(10):59-61.

