于探索规律中培养学生的数学核心素养

    陈兴长

    

    

    

    [摘要]数学核心素养包括很多内容，主要归纳為数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析，《关于全面深化课程改革落实立德树人根本任务的意见》和《义务教育数学课程标准》均提出了发展学生核心素养的要求，可见，我国的数学教育将核心素养的培养又提到了新的高度，然而，数学核心素养并非只能使用简单的方式教授给学生，它可在教育教学的各个环节中加以渗透，规律探究问题是初中数学教学中的一种重点题型，如何在规律探究教学中渗透核心素养培养尤为重要，文章就初中数学若干类规律探究问题教学中如何渗透数学核心素养培养进行分析。

    [关键词]规律探究;核心素养;初中数学

    [中图分类号]G633.6 [文献标识码]A [文章编号]1674-6058（2020）05-0030-02

    一般来讲，规律探究问题是指给出一组具有某种特定关系的数、式、图形，再给出有限的几项题目情景，或是给出与图形有关的操作、变化过程，要求学生通过观察、分析、推理，探索其中所蕴含的规律，进而归纳或猜想出共同特征，或者发现其中的变化趋势，在解答过程中需要经历观察、归纳、猜想、实验、证明等数学活动，以加深学生对相关数学知识的理解，从而认识数学知识之间的联系，在此过程中，学生数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析等核心素养得到了发展。

    下面将笔者在规律探究问题教学中培养学生数学核心素养的几点思路与大家分享。

    一、在图形变化类规律探究中培养学生的数学抽象与逻辑推理素养

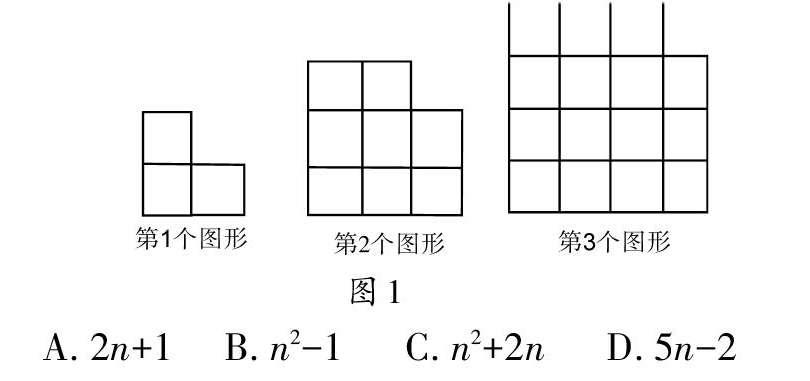
    【例1】用大小相等的小正方形按一定规律拼成下列图形（如图1），则第n个图形中小正方形的个数是（ ）。

    分析：由第1个图形中小正方形的个数是22-1、第2个图形中小正方形的个数是32-1、第3个图形中小正方形的个数是42-1可知，第n个图形中小正方形的个数是（n+1）2-1.化简可得答案C。

    本题有两个主要步骤：（1）将图形抽象成数量;（2）观察每个图形对应数量之间的变化关系，在教学过程中，我们应注意引导学生思考：每个图形中各有几个图形？各个图形中图形的数量怎么表示？每个图形对应的数量之间存在怎样的关系？通过此类问题的训练，让学生学会把生活中具象化的事物的量对应成数，逐步形成抽象能力，通过观察、比较、归纳、猜想及推理证明得出不同图形之间的数量关系，逐步形成逻辑推理能力。

    解决此类问题需要做到：（1）能正确地感受出翻折前与翻折后图形的形状;（2）能准确地观察出翻折前与翻折后图形两者之间的边长关系，这就需要学生有较好的直观想象能力以及逻辑推理能力，只有这样，学生才能准确无误地判断出图形之间的变化关系，在平时的数学教学中，只要教师能针对不同类型的翻折问题加强训练，就可以培养学生的直观想象能力以及逻辑推理能力。

    三、在数字变化类规律探究中培养学生的逻辑推理及数学运算素养

    学生在解决此类问题时需要通过观察各个等式左右两边的关系，及各个等式之间的数量变化关系，加以归纳、猜想、计算及证明等，借助此类问题可以让学生在思考观察中不断增强逻辑推理及数学运算能力。

    总之，规律探索问题，设计独特、新颖，蕴含着丰富的数学思想方法，需要学生通过观察、思考、分析所给的已知数、式或图形的变化规律，并加以推理、归纳、猜想及证明计算等，规律探索问题符合学生的认知规律，是训练、考查学生思维的灵活性和深刻性的创新题型，解决规律探索问题，不仅能使学生感受数学文化，拓宽数学视野，提高数学核心素养，还能帮助学生实现从模仿到创新的思维发展。