例谈统计图表的综合运用
韩贤

[摘要]探寻中考统计图表的考查形式,分析与解读统计图表典例,以培养学生的数据分析意识与应用意识.
[关键词]统计图表;综合运用;初中数学
[中图分类号]G633.6? [文献标识码]A? [文章编号]1674-6058(2020)02-0020-02
新课程标准要求让学生经历实际问题中收集和处理数据、利用数据分析问题、获取信息的过程,掌握统计与概率的基础知识与基本技能.统计图表就是对实际问题中的数据进行收集、整理与表达,它包括条形统计图、扇形统计图、折线统计图、频率直方图和频率统计表等.在解题中,要求学生正确地识图、读图、画图,能提取有用的信息,综合各方面信息,并通过信息的梳理与观察发现规律、提出合理化建议等.那么统计图形有哪些综合运用呢?
一、扇形统计图与条形统计图的综合运用
当扇形统计图与条形统计图结合时,扇形统计图上会标出各部分所占的百分率,而各部分百分率之和为1,可以利用其他部分的百分率得出所求部分的百分率.在条形统计图上会标出各部分的具体频数,而各部分频数之和等于总数,可以利用其他部分的频数得到所求部分的频数,这两者结合可求得总数.
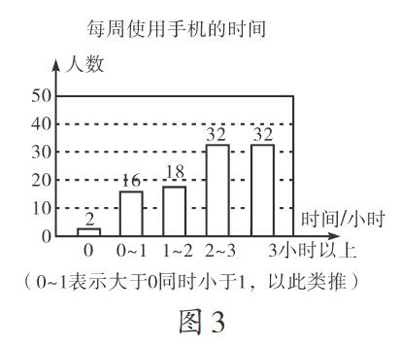
[例1]为了解学生手机使用情况,某学校开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查,并绘制成如图1和图2的统计图,已知“查资料”的人数是40人.
请你根据以上信息解答下列问题:
(1)在扇形统计图中,“玩游戏”对应的百分比为??? ,圆心角度数是??? 度;
(2)补全条形统计图;
(3)该校共有学生2100人,估计每周使用手机时间在2小时以上(不含2小时)的人数.
分析:(1)根据题意,得“玩游戏”对应的百分比为1-(40%+18%+7%)=35%,则“玩
游戏”对应的圆心角度数是360°x35%=126°.
(2)根据题意得40÷40%=100(人),∴玩手机3小时以上的人数为100-(2+16+18+32)=32(人),补全图形如图3.
(3)根据题意得2100×{(32+32)/100}(人).
每周使用手机时间在2小时以上(不含2小时)的人数有1344人.
二、折线统计图与统计表的综合运用
折线统计图也标识了各部分的频数,这一点与条形统计图相同.不同的是折线统计图将频数连起来,使我们可以清楚地看出事物变化的趋势.统计表一般是指频数与频率统计表,从中可以读出频数与频率,频数与频率两者结合可以得出总数及未知频数与频率.折线统计图与统计表结合,可以将统计表的数据在折线统计图中直观地显示出来.
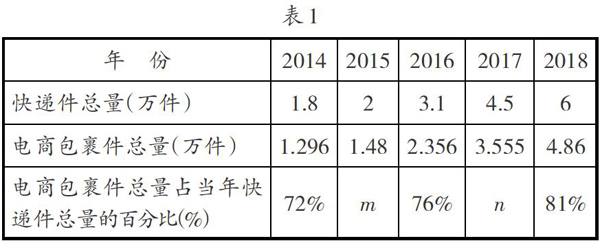
[例2]近年来,随着电子商务的快速发展,电商包裹件总量占当年快递件总量的比例逐年增长.根据某快递公司某网点的数据统计,得到如表1所示的统计表.
(1)直接写出m,n的值,并在图4中画出电商包裹件总量占快递件总量百分比的折线统计图;
(2)若2019年该网点快递件总量预计达到7万件,请根据图表信息,估计2019年电商包裹件总量约为多少万件
分析:(1)m=1.48÷2=74%;n=3.555÷4.5=79%;折线统计图如图5所示.
(2)从增长的趋势看,每年的百分比比上一年增长2%左右,故2019年电商包裹件总量占当年快递件总量百分比约为83%,2019年电商包裹件总量约为7x83%=5.81(万件).
三、频数分布直方图、频数分布表与扇形统计图的综合运用
频数分布直方图与条形统计图类似,所不同的是频数分布直方图横轴的数据是连续的,而條形统计图是不连续的,从这两种图上都可以获得各部分的频数.实际上数据的整理过程,先收集数据,再整理成统计表,继而根据表达的需要,绘制成直方图、条形图、扇形图或折线图,所以统计图的数据来自统计表.
[例3]我市为加强学生的安全意识,组织了全市学生参加安全知识竞赛.为了解此次知识竞赛成绩的情况,随机抽取了部分参赛学生的成绩,整理并制作出如表2和图6所示的不完整的统计表和统计图,请根据图表信息解答以下问题.
(1)一共抽取了??? 个参赛学生的成绩;表中a=??? ;
(2)补全频数分布直方图;
(3)计算扇形统计图中“C”对应的圆心角度数;
(4)某校共2000人,安全意识不强的学生(指成绩在70分以下)估计有多少人?
分析:(1)总人数=14÷35%=40(人),a=40-8-12-14=6,故答案为40,6;
(2)频数分布直方图如图7所示;
(3)扇形统计图中“C”对应的圆心角度数=360°×12/40=108°;
(4)200×(6/40)=300(人)安全意识不强的学生(指成绩在70分以下)估计有300人.

