基于改进遗传算法的应用研究
郭来军
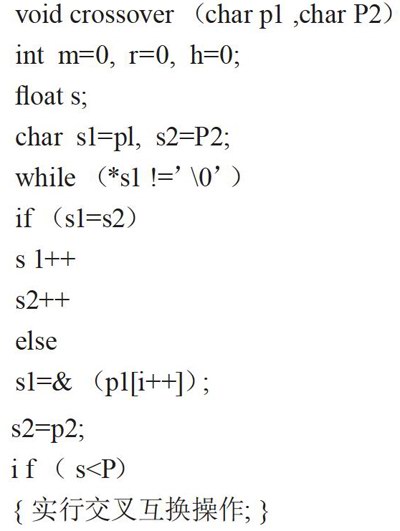
摘要:在计算机技术的研究中,关于遗传算法的应用研究是热门的课题。目前,随着社会经济的不断发展,遗传算法被应用到人们生活的很多领域。文章对遗传算法基本概念及工作原理进行了分析,对遗传算法在实际应用中存在的收敛速度和局部最优之间的矛盾问题,提出了遗传算法的改进方法。
关键词:遗传算法;计算机技术;选择算子;编译算子
遗传算法是一种全局优化随机搜索算法,遗传算法是对自然界中生物遗传进化的过程进行模仿的一种原理。传统的遗传算法在工业设计和交通运输等方面都得到了广泛的应用,但是遗传算法存在局部最小和过早收敛的矛盾问题为了让遗传算法更好地被应用,本文对遗传算法中的3种基本遗传算子进行了研究。在遗传算法的遗传算子的研究中对遗传算子参数的选择决定了遗传算法的全局性能,遗传算子参数选择的合理性是遗传算法全局优解的关键。
1遗传算法的概念及原理
1.1遗传算法概念
遗传算法中的遗传因子也叫作基因,其承载着很多遗传信息,基因是用来控制生物特征的最基本的遗传单元,生物体通过基因把遗传信息传递给下一代,在遗传算法中利用的就是基因的这个特点。在遗传算法中的基因是一个二进制数或者字符等,通过计算机对基因的整个操作过程进行模拟,在遗传算法中基因是最基本的构成单元。染色体是基因的载体,也是遗传信息的重要载体,染色体是生物中最有价值的部分。在遗传算法中染色体也是重要的部分,遗传算法对染色体进行编码,编码采用二进制码的方式,二进制码使用简单,二进制码和生物体的染色体非常相似,在遗传算法中进行遗传的操作非常方便。种群是生物个体组成的群体,在遗传算法中种群是所有染色体的总和,在遗传算法中染色体是个体,在遗传过程中的某一代中的染色体的总和构成种群。在遗传算法中种群为遗传进化的搜索提供空间。在遗传算法中,先对种群中的染色体进行编码,这样就可以得到每一个染色体对应的编码,每个个体就是实际中的一个解,每个解都和函数值相对应,其中适度函数影响着遗传算法中的收敛速度等性能[2]。
1.2遗传算法的基本算子
选择算子是遗传算法中的基本算子之一,通过选择算子遗传算法可以模拟大自然物种的自然选择方式,选择算子是通过适度函数来对种群的个体进行选择,根据个体的适应度值的高低把种群中优良的个体选择到下一代种群中,个体的适应度越高被选择的可能性就越大。选择算子保证了种群向适应度高的方向发展,其决定遗传算法的收敛性,还可以保证遗传算法中种群的多样性。选择算子的有效设计可以保证遗传算法具有更局的收敛速度。
交叉算子在遗传算法中起到决定性的作用,在遗传算法中通过交叉算子可以得出比父代更加优秀的个体,这样可以更快地得出最优解。交叉算子中交叉概率对遗传算法的影响很大,交叉概率大不利于对最优解的计算,交叉概率小对算法的搜索能力就降低了,得到最优解的概率也变小了,所以对交叉算子概率的选择要仔细考虑。
变异算子是遗传发生变化的主要根源之一,在遗传算法中变异算子是解决局部收敛的最有效办法。遗传算法中交叉算子决定全局搜索能力,变异算子作为主要的辅助,完成对空间的局部搜索,交叉算子和变异算子的有效结合可以提高遗传算法的最优解的求解性能[3]。
2基于改进遗传算法的应用研究
对遗传算法的改进研究是基于3个基本的遗传算子,分别是选择算子、交叉算子和变异算子[4-5]。
2.1选择算子的改进
传统的遗传算法中比较常用的选择方法是轮盘赌选择,这种选择方式比较直观而且简单,轮盘赌选择是把种群中所有的个体都进行累加,这樣就形成了种群的总适应度,之后对种群中的个体进行相对适应度的计算,通过计算可以在选择之前就得出一个随机数,然后就可以根据个体的相对适应度作为选择依据来对个体进行选择。在选择方式中,适应度的个体越大,个体被选择的机会就更大。轮盘赌选择方式使用比较普遍,但是在选择的时候还是存在一些问题。针对问题提出了对选择算子的改进,要对种群中所有的个体进行排序,按照个体适应度的高低进行排列。对排列完的个体分成4个等份,把适应度低的排在后面,按一定的比例进行淘汰,不进入到下一代;把适应度中等的排在中间按2/4的比例把个体拷贝出来,作为下一代;适应度高的排最前面拷贝成两份,都选择到下一代中。这样经过选择后,下一代的种群数量相等。这样的选择算子的改进办法可以把适应度低的个体直接淘汰,提高了遗传算法的收敛速度。种群中适应度高的个体数量增加,遗传算法更加高效,这样可以有效地解决前面提到的选择的问题。
2.2交叉算子的改进
交叉算子作为遗传算法中重要的操作性算子,交叉算子对遗传算法的收敛性起着重要的作用,而且可以提高遗传算法的收敛速度。所以需要设计一个有效的交叉算子来提高遗传算法的性能。交叉算子的改进方法,更好地保护亲代个体的优良基因,提高遗传算法的性能,在交叉算子中引入相似度的概念,利用两个父体之间相识度值的大小来决定是否进行交叉操作。假设两个编码是二进制的父体,分别是X,Y,相识度是S,交叉临界值为R,如果父体的相识度值大于交叉临界值,那么两个父体不可以进行交换,这样它们的优良基因模式就不会被破坏了,如果父体的相识度值小于交叉临界值,那么两个父体可以进行交换。本文对两个父代个体的共同子串长度程序代码设计如下:
2.3变异算子的改进
在最基本的遗传算法中,变异的概率值作为一个常数是不变的。如果变异概率在遗传进化中不发生变化,那么种群适应度和最优的个体适应度相似,遗传进化就没有竞争性了,进化速度就会降低,种群多样性也会减少,局部收敛情况很容易发生,严重影响算法的运行效率。变异概率值应该根据遗传算法进行适当调整,这样遗传算法就可以具有躲避局部收敛的能力,使算法的效率得到提高。我们采取的改进措施是尽量减少对种群优秀模式破坏的可能性,并生成有效的和优秀的模式。变异个体的适应度的值比种群评价适应度的值大,那么个体变异的概率就小,这是符合生物进化规律的,个体的适应度越大,发生变异的情况就小,这样可以避免优良个体被破坏。如果变异个体适应度值比种群平均适应度的值小,那么个体不是优良的,不适合生存。所以个体的变异率越大,个体的优良品种越多,这样可以提高算法的局部搜索能力,更可以加快全局收敛,从而改进遗传算法的性能。
3结语
传统的遗传算法交叉率是固定的,收敛速度慢。本文通过对遗传算法中选择算子、交叉算子和变异算子的改进,提高了遗传算法跳出局部的收敛能力和遗传算法的收敛速度,并且缓解了收敛速度和局部最优解之间的矛盾。基于改进遗传算法的应用研究在遗传算法中具有一定的应用价值。
[参考文献]
[1]单錦辉,高友峰,刘明浩,等一种新的变异测试数据自动生成方法[J].计算机学报,2008(6):1025-1034.
[2]刘铁男,刘斌,梁福责一种带局部搜索策略的遗传算法及其应用[J].大庆石油学院学报,2005(2):76-78.
[3]杨晓华,陆桂华,杨志峰,等格雷码加速遗传算法及其理论研究[J].系统工程理论与实践,2003(3):100-106.
[4]潘俊辉,王辉.一种基于改进的遗传算法的关联规则挖掘及应用[J].齐齐哈尔大学学报(自然科学版),2011(2):11-14.
[5]刘伟,朱珍民,蒋发群,等普适计算中一种最优服务选择算法的设计与仿真[J].计算机应用研究,2010(3):899-903.

