把握关键教学点 有效开展总复习
林淑金


[摘???要]准确选择初三总复习“关键教学点”能有效解决初中数学总复习中存在的难点问题,有助于教师探索提高初中数学总复习教学质量的新途径和新方法.初三数学总复习关键教学点的选择要紧扣数学核心素养,以使学生的学习能力不断提升.
[关键词]初三数学;总复习;关键教学点;三角形;中位线
[中图分类号]????G633.6????????[文獻标识码]????A????????[文章编号]????1674-6058(2019)35-0025-03
复习课非平常课,复习目标要具体明确、直接到位,对知识的梳理不能是简单地回顾重复,而是要加深知识间的内部联系,要以点带面,进行逻辑连接,要有思想方法的渗透、归纳、总结和提升.下面笔者以“三角形之中位线和中线”的复习为例,探讨对复习关键教学点的选择、实施和思考.
一、将“三角形之中位线和中线”设置为复习关键教学点的理由
“三角形之中位线和中线”是初中数学的重要知识,其包含的基本图形和渗透的几何解题方法是中考数学的高频考点.考试大纲对这部分内容提出了比较高的要求:理解三角形的中线,能用文字语言、符号语言和图形语言解释三角形的中线;探索并证明三角形的中位线定理、直角三角形的性质定理,能将三角形问题转化为四边形问题来解决,渗透化归与转化的数学思想.
将“三角形之中位线和中线”设置为复习关键教学点,有助于提高学生的逻辑推理、直观想象等数学核心素养.对定理证明的再回顾,有助于学生构建数学知识体系.直观想象能引导学生发现和提出问题、分析并解决问题,探索并形成论证思路、进行逻辑推理,增强运用图形思考问题的意识.
二、“三角形之中位线和中线”复习教学设计
(一)学情分析
学生已经学习了三角形、四边形等几何知识,能认知相关概念与性质,初步具有几何直观、应用意识和一定的逻辑推理能力,基本掌握了几何图形研究的一般思路和方法,但是对定理的证明以及定理证明过程中渗透的几何解题方法及辅助线的作法缺乏系统的归纳,对于需要作辅助线的几何题往往无从下手,找不到解题突破口.
中考复习时间紧、内容多,如果盲目地刷题,没有及时地归纳总结只会事倍功半.通过“三角形之中位线和中线”的复习,可让学生一见“中点”就能利用倍长中线法和构造中位线法构造三角形全等,从而证明线段间的数量关系,找到解题的突破口,有效提高了学生的思维能力和解决问题的能力.
(二)教学重难点
重点:三角形中位线和中线性质的应用,以及通过复习定理证明过程,挖掘证明过程中渗透的倍长中线法和构造中位线法.
难点:几何证明中辅助线的作法.
(三)教学目标
(1)加深对已知条件带中点决定的三角形线段间的数量关系的理解,熟练应用三角形中位线定理及直角三角形的斜边中线性质,强化训练涉及重要知识点的中考题型.
(2)回顾定理的证明过程,归纳倍长中线法;思考完成例题,提高解决问题的能力,进一步提升几何直观、逻辑推理等数学核心素养.
(四)教学过程
1.“中”字引课,梳理中位线、中线及相关定理
问题1:看到“中”字,你会想到什么?
学生回答:中点,中位线(多个中点),中点四边形(多条中位线),中线,中(重)心(多条中线),等等.
问题2:这个“中”字和哪个数字有密切的关系?请举例说明.
学生可能会说2和[12]这两个数字.所举的例子有:已知点A是线段BC的中点,那么AB=AC=[12]BC(初中最早学的一组因果关系);已知AD为△ABC的中线,那么S△ABD=S△ADC=[12]S△ABC?,等等.只要学生所举的例子是合理的,教师都应该给予肯定.
问题3:你能回忆起几个有关三角形中点,并包含线段[12]数量关系的定理或结论?
学生回答:(1)三角形的中位线定理;(2)直角三角形的中线性质定理;(3)含30°角的直角三角形的直角边和斜边的关系;(4)等腰三角形的“三线合一”.
【设计意图】前3个问题通过中文字面理解,揭示“中”与“[12]”数量关系之间的联系,借此调动学生的学习积极性,激发学习的复习兴趣.
问题4:你可以画出这些定理或结论对应的基本图形吗?
学生所画的图形:
【设计意图】鼓励学生动手画图,实现由文字语言到图形语言的转化,增强了学生对图形的直观意识.
问题5:对于定理的直接应用,你能熟练掌握吗?
(教师展示三道中考题供学生训练)
中考题1.如图2,平行四边形ABCD的周长为28,对角线AC,BD相交于点O.点E是CD的中点,BD=10,则△DOE的周长为(????????).
A.?28B.?24C.?12D.?17
考点分析:平行四边形的性质和三角形的中位线定理.
中考题2.?如图3,在Rt[△]ABC中,D,E,F分别为AB,AC,AD的中点,若BC=2,则EF的长度为(????????).
A.?[12]?????????????????????B.?1
C.?[32]?????????????????????D.?[3]
考点分析:直角三角形斜边上的中线,三角形的中位线定理.
中考题3.如图4,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD=60°,则△OCE的面积是(????????).
A.?[3] B.?2 C.?[23] D.?4
考点分析:三角形的中位线定理,菱形的性质,相似三角形的判定与性质.
【设计意图】通过2018年各省市的中考高频考题,明确三角形中位线及中线的相关定理的考点.三个问题有一些梯度,但又不是太难,应该成为学生平时训练的重点题型.
2.回归课本,启迪新思路
问题6:这3个常用的“[12]”定理是怎么证明它们的正确性的?画出图形试试看.
【设计意图】引导学生画出三个定理证明的图形,强调动手画图的重要性.
问题7:大家有没有发现这三个定理的证明过程非常相似?相似点在哪里?
【设计意图】设置问题引导学生结合图形归纳出几何证明的常用方法,同时让学生领悟辅助线的作法,尤其是倍长中线法.
问题8:已知三角形的两边AB,AC分别为8和6,则第三边BC的中线AD的取值范围是.对于此题,你打算从何入手?突破口在哪?
【设计意图】只给题不给图,再一次强调动手画图的重要性.通过这个问题的解决,让学生理解与掌握倍长中线法和构造中位线法这两种重要辅助线的作法.通过一题多解,及多个图形的展示开阔学生的作图视野.
学生独立作图解答,教师巡视观察并遴选典型图形(如图6),让学生画到黑板上.归纳概括两种辅助线作法:倍长中线法和构造中位线法.
3.典例分析,拓展提升
【例题】如图7,?∠BAC=∠DAE=90°,AB=AC,AD=AE,连接BE、CD,M为BE的中点,连接AM,求证:CD=2AM.
证法1:如图8,证明△ACD?≌△ABA′.
证法2:如图9,证明△ACD?≌△EA′A.
【设计意图】利用全等三角形中非常典型的手拉手模型为基本图形,引导学生证明线段“[12”]数量关系.通过一题多解再一次明确倍长中线法和构造中位线法两种辅助线的作法.这道题综合性较强,通过教师对图形的分解讲解,降低难度,使学生能找到入手点,厘清证明过程,提高逻辑推理能力.
4.课堂练习,巩固辅助线的作法
(1)如图10,在△ABC中,CD平分∠ACB,AD⊥CD于D,E是AB中点,AC?=?15,BC?=?27,求DE的长.
(2)如图11,点[E]是[BC]的中点,[∠BAE=∠CDE],求证:[AB=CD].
【设计意图】第一题通过延长AD,利用等腰三角形的三线合一构造中位线,第二题通过倍长AE,找全三角形全等的条件,进而证明线段相等.两道练习题的设置意在锻炼学生自己动手解题的能力,提高学生“见中点则作辅助线”的意识,进而提高学生的解题能力.
5.课堂小结,归纳提炼
先让学生谈谈本节课的感受,教师再进行课堂小结:几何辅助线作法,其实是化归与转化思想的应用,一般是将三角形的线段问题转化为三角形全等或是特殊的四边形的问题来解决.再次强调辅助线作法:倍长中线和构造中位线.用“见中线则倍长,构造全等证相等”“中点中点连成线,一半平行就出现”来巩固学生对辅助线作法的记忆.
6.课后作业
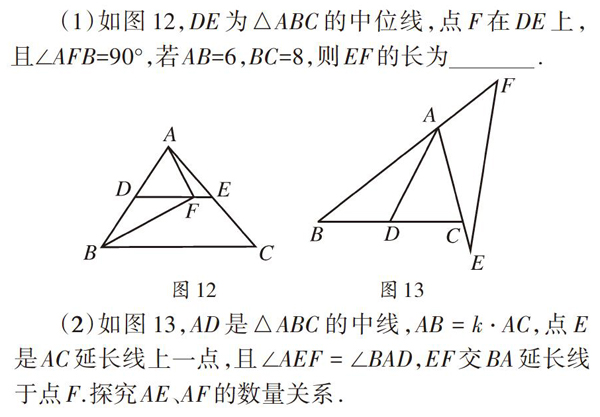
(1)如图12,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=6,BC=8,则EF的长为??????????????.
(2)如图13,[AD]是△[ABC]的中线,[AB=k?AC],点[E]是[AC]延长线上一点,且[∠AEF=∠BAD],[EF]交[BA]延长线于点[F].探究[AE]、[AF]的数量关系.
三、初三数学总复习教学关键点的选择和设计引发的思考
总复习关键教学点的设计定位要精确且切合实际,不可好高骛远,华而不实.有辅助线的几何题是学生掌握知识的薄弱之处,他们大多时候不清楚为什么要那样作辅助线,怎么想到要作辅助线才能简化问题,因此对几何辅助线问题的复习教学应从课本定理出发,引导学生从已知条件中联想到作辅助线的合理性,再通过一类问题的技能固化,加深学生对这类辅助线的理解和应用.
数学课堂应该是充满疑问和解答的课堂,教学过程中教师应有效设置问题串,引导学生深度思考,有针对性地铺垫关键点教学,促進学生在回答问题的过程中产生新的问题,从中学会发现问题、提出问题和解决问题.这是理想中的课堂,充满着智慧的火花,也是我们一直所追求的复习课堂.
[??参???考???文???献??]
蒲锦泉.以素养立意的数学课堂教学思考:以《方程的根与函数的零点》教学为例[J].福建基础教育研究,2018(1):87-89+95.
(特约编辑 安 平)

