基于RSSI和遗传算法的无线定位方法及其实现
孙建领+张宏钦


摘 要:随着无线电技术的发展,无线传感器网络在目标跟踪、环境监测、空间探索等领域得到广泛应用,节点定位技术在无线传感器网络中具有重要地位。文章提出了基于遗传算法的无线定位算法,解决了基于RSSI信号强度的无线定位方法定位精度较低的问题。该算法采用考虑参考节点RSSI信号波动误差的质心算法进行种群初始化,使用基于记忆搜索方向的交叉机制和自适应调整搜索半径的策略,为下一代种群的搜索方向及搜索半径提供有效的指导信息。实验结果表明,该算法的定位精度明显高于典型及改进的极大似然估计定位算法,有效地提高了定位精度。
关键词:无线定位;遗传算法;接收信号强度
1 无线传感器研究背景
无线传感器网络(Wireless Sensor Network,WSN)是由大量的微型传感器节点组成的数据网络系统,主要用于在网络覆盖范围内进行信息的采集、分析和处理,并能够最终将关键数据返回给控制中心。无线传感器网络的定位技术就是先通过获取未知坐标节点与已知坐标的参考节点之间的距离等信息,再通过某种定位算法来计算出未知节点坐标的技术[1]。它可以广泛应用于灾难救援、智能城市、交通管理、环境监测、医疗卫生、国防军事等诸多领域。
WSN的定位方法主要有基于信号到达时间(Time of Arrival, TOA)、到达时间差(Time Difference of Arrival, TDOA)和基于接收信号强度指示(Received Signal Strength Indicator, RSSI)的定位方法。TOA和TDOA 测距技术利用信号的传播速度和传输时间作为输入来计算距离,其定位准确度高,要求高精度的时钟实现同步,成本较高;RSSI测距技术利用理论或经验模型,将信号传播损耗映射为传播距离,从而实现定位,具有低功耗、低成本等优点[2]。RSSI信号易受反射、多径、障碍物等因素的影响,易于产生信号强度的波动[3],在非视距环境下会出现较大的定位误差[4-5],因此该定位方法目前多应用在区域级别的定位领域,定位精度相对较低。为了提高定位精度,文献[6]提出了基于RSSI信号强度的质心定位方法,该方法根据参考节点对盲节点的不同影响力来确定加权因子,存在将非线性问题转换为线性问题后定位的值域未能完整地覆盖原始定位问题模型值域的问题。文献[7]提出了改进的极大似然估计定位方法,该方法使用最速下降算法对极大似然估计算法所得的节点定位值进行优化,存在将非线性模型转换为线性模型的误差问题。
遗传算法是借鉴生物界“适者生存”原則的优化算法[8],其目标函数的定义域可以为任意集合且不会受到连续可微的约束,这种特点使得遗传算法非常适合求解定位问题,避免了典型定位算法中值域转换及从非线性模型转换为线性模型时产生的定位误差[9]。
基于RSSI和遗传算法的无线定位算法采用考虑参考节点RSSI信号波动误差的质心算法进行种群初始化,具有记忆搜索方向和自适应调整搜索半径的特点,能为下一代种群的搜索方向及搜索半径提供有效的指导信息,可以有效地提高无线定位的精度。将WSN中需要定位的节点称为盲节点,而将已知坐标位置并能协助盲节点进行定位的节点称为参考节点。
2 典型的定位算法存在的问题
典型的定位应用通常使用改进的质心法或极大似然估计法来确定坐标位置,通过对这两种定位算法进行分析后发现以下问题。
使用典型或改进的质心算法进行定位坐标计算时,最终计算的定位坐标位置必然限定在由几个顶点所围成的凸多边形内部,这是由质心算法的几何性质所决定的。当仅有3个顶点时,凸多边形即为三角形区域,其中一种情况如图1所示。
虽然根据算法的不同可以选择不同的顶点作为凸多边形的顶点,但在使用RSSI信号强度方法进行定位时,由于RSSI信号测距误差的大小与距离成正比,且经过实测后发现测距误差是非线性的,因此无论选择哪些点作为凸多边形的顶点,其所围成的凸多边形区域均不能覆盖最终定位坐标的全部值域。而由多个参考节点的RSSI信号测距误差圆环所组成的不规则扇形区域覆盖了定位坐标的全部值域,如图2所示。图中箭头所指处为在给定的测距误差条件下定位误差值最小的坐标点,而该点并不在图1所示的凸多边形区域内部。使用质心算法进行定位计算,实际上是将非线性问题转换为线性问题进行求解,虽然降低了问题求解的难度,但未能完整地覆盖原始问题模型的值域,因此定位结果的误差较大。
使用典型的极大似然估计法进行定位坐标计算时,由于未考虑RSSI信号强度波动引起的测距误差,会将各参考节点置为相同的可信度,忽略不同参考节点的测距误差值,从而降低了定位的精度。即便使用改进的考虑RSSI测距误差的极大似然估计法,也存在从非线性模型转换为线性模型的误差问题[10]。
使用遗传算法求解定位问题可以避免上述问题。首先,遗传算法的目标函数的定义域可以为任意集合且不会受到连续可微的约束,能够完整地覆盖原始问题模型的值域,可以通过对待解决的问题进行分析并设计合理的适应度函数对其值域进行有效控制;其次,使用遗传算法可以避免典型定位算法中从非线性模型转换为线性模型时产生的定位误差[9]。上述特点使得遗传算法非常适合求解定位问题,将使用遗传算法对定位结果进行全局优化。
3 基于遗传算法的定位算法
采用RSSI方法进行定位需要获取盲节点与多个参考节点之间的实测距离,由于RSSI信号在实际传播过程中受环境影响会造成信号衰减,与理论或经验模型有一定偏差,导致以各参考节点为圆心、以各自测距为半径的圆,并未相交于同一交点。为了降低定位误差,需要对已获得的多个带有误差的RSSI距离值进行全局优化计算,再计算出定位结果。因此,基于RSSI测距的无线定位方法是多约束条件下的优化问题。
由于遗传算法在求解多约束条件下的组合优化问题有其独特优势,具有文章前面所述的诸多优点,将使用改进的遗传算法来求解待定位结点的坐标。
3.1 种群初始化
先使用考虑参考节点RSSI信号波动误差的加权质心算法对种群进行初始化,再使用记忆搜索方向并自适应调整搜索半径的向量交叉机制进行交叉操作。
在室内办公环境下使用基于CC2500无线通信模块的收发设备经过多次实测后,使用极大似然估计法计算出RSSI信号波动引起的测距误差与实测距离的关系为:
其中efi(error of fluctuation)为参考节点i的RSSI信号波动引起的测距误差,disti为未知位点与参考节点i的实测距离,reliabilityi为参考节点i的测距可信度,可信度越高表明该参考节点的测距精度越高。
优秀的初始种群可以加快整个群体向最优解的进化速度,这就需要在考虑算法关键因素的情况下使用较小的时间复杂度进行计算。此处采用考虑参考节点RSSI信号波动误差的质心算法来初始化种群。种群初始化的步骤如下:
(1)从多个参考节点中按测距可信度从高至低选出不在同一直线上的3个参考节点。
(2)以3个参考节点坐标为圆心,以各自的实测距离为半径获得各圆之间的交点。当有两个交点时,选择与另一个参考节点距离较近的交点作为待加权坐标点,3个参考节点共可获得3个待加权坐标点。此时可能会出现两种两圆无交点的情况:
其中ri为参考节点i的实测距离。此时需要对两个参考节点的RSSI信号波动误差按可信度进行等比缩放,以使两圆有唯一交点,将该交点作为待加权坐标点。缩放率rate按公式(3)计算获得:
经过上述操作后已获得3个待加权坐标点,再按公式(4)计算其权值:
其中i,j表示不同的参考节点,weightij表示由参考节点i和参考节点j的测距值为半径所得到的待加权坐标点的权重。
(3)按公式(5)和(6)计算考虑参考节点RSSI信号波动误差的质心点坐标:
其中Δv为对质心坐标增加的微幅随机扰动参数,以此来保证初始种群的多样性。accurate为用户要求的定位精度,nodeSize为参考节点的数量。重复上述步骤popSize次,即完成了个体数量为popSize的种群初始化。还需计算出公式(5)和(6)中的不包含Δv参数时的一组基准质心坐标,用于保存对后续的向量交叉操作进行指导的初始化信息。
3.2 适应度函数
适应度函数是用来衡量群体中的个体优秀与否的标准,它必须能够反映出个体的优秀程度:优秀的个体其适应度值较大,而性能差的个体则适应度值较小。此处采用基于信标可信度的加权质心原理,将适应度函数按如下公式进行定义:
在种群的每一代进化过程中,先使用公式(8)计算个体的适应度值,再将种群中的个体按照适应度值由高到低进行排序。当两个不同个体的适应度值相同时,再通过公式(9)计算附加适应度值并进行比较。公式(8)是坐标点在测距误差区域外部时的适应度值,公式(9)是坐标点在测距误差区域内部时的适应度值。
3.3 选择、交叉、变异
首先从群体中选出Nbest个适应度最高的个体,将这些个体直接遗传到下一代群体中,以此来保证进化过程中某一代的最优解不被交叉和变异操作所破坏。其余的个体则由交叉操作生成。考虑到适应度较高的两个个体交叉后生成优秀个体的概率较大,此处先以个体适应度占种群适应度的百分比为概率选出两个父个体Ta,Tb,再进行交叉操作。个体Ti被选中的概率Pi按公式(10)计算。
其中概率Pi反映了个体i的适应度在整个群体的个体适应度总和中所占的比例,即第i个个体被选中的概率与其适应度的值成正比。
在二维空间条件下,为了增加个体搜索到适应度更高的坐标点的概率,文章采用了记忆搜索方向的向量交叉机制。每一个个体都包含一个记忆搜索方向的向量,该向量始终由某个父个体的坐标点指向当前个体的坐标点,用于记录当前个体在进化过程中的搜索方向及步长信息。在种群初始化时将该向量设为由基准质心坐标点指向当前个体的坐标点。对于父个体Ta,Tb,交叉操作的主要步骤如下:
将两个父个体的记忆搜索方向的向量,分别以自身向量为基准,以与另一向量的最小角度差为限制范围,按与旋转度数成反比的概率对自身向量进行旋转,以此增大在记忆搜索方向上搜索的概率,再将向量的模型以两个向量的差为限制范围进行随机缩放,以此对搜索半径进行自适应调整,如图3所示。此时将两个父个体的坐标与新生成的两个向量进行累加产生两个新的子个体,然后计算这两个子个体的适应度值并与两个父个体进行比较,将适应度较大的两个个体复制到新的种群中去,以确保整个群体的平均适应度呈非递减状态。变异采用与交叉类似的机制,通过对个体自身的记忆搜索方向的向量进行偏角旋转来实现。
可以采用以下3种方式中的一种来决定算法何时停止运行。
(1)最優个体的适应度值连续指定代数未更新。此时说明种群的进化已趋于稳定。
(2)限定算法运行指定的时间,例如限定算法只运行200 ms。该方法可通过限定算法的运行时间来为系统提供额外的休眠时间,以达到节省设备电能、延长设备使用时间的目的。
(3)指定算法中群体进化的代数。
最后,选出最优个体的坐标值作为最终的定位坐标。
4 实验结果与分析
考虑到后续功能及协议扩展的灵活性,采用可定制通信协议的CC2500芯片和STM32处理器,并自行设计并实现了相关的通信协议。
CC2500是低成本真正单片的2.4 GHz收发器,为低功耗无线应用而设计。电路设定为2 400~2 483.5 MHz的ISM(工业、科学和医学)和SRD(短距离设备)频率波段。RF收发器集成了一个数据传输率可达500 kbps的高度可配置的调制解调器。具有高灵敏度(10 kbps下-98 dBm,1%数据包误差率)、可编程控制的输出功率(可达+1 dBm)、数字RSSI 输出等特性。通过向基于CC2500芯片的无线收发设备写入不同的代码,可以在不改变硬件设备的条件下分别实现参考节点、盲节点和中心节点的各自功能。
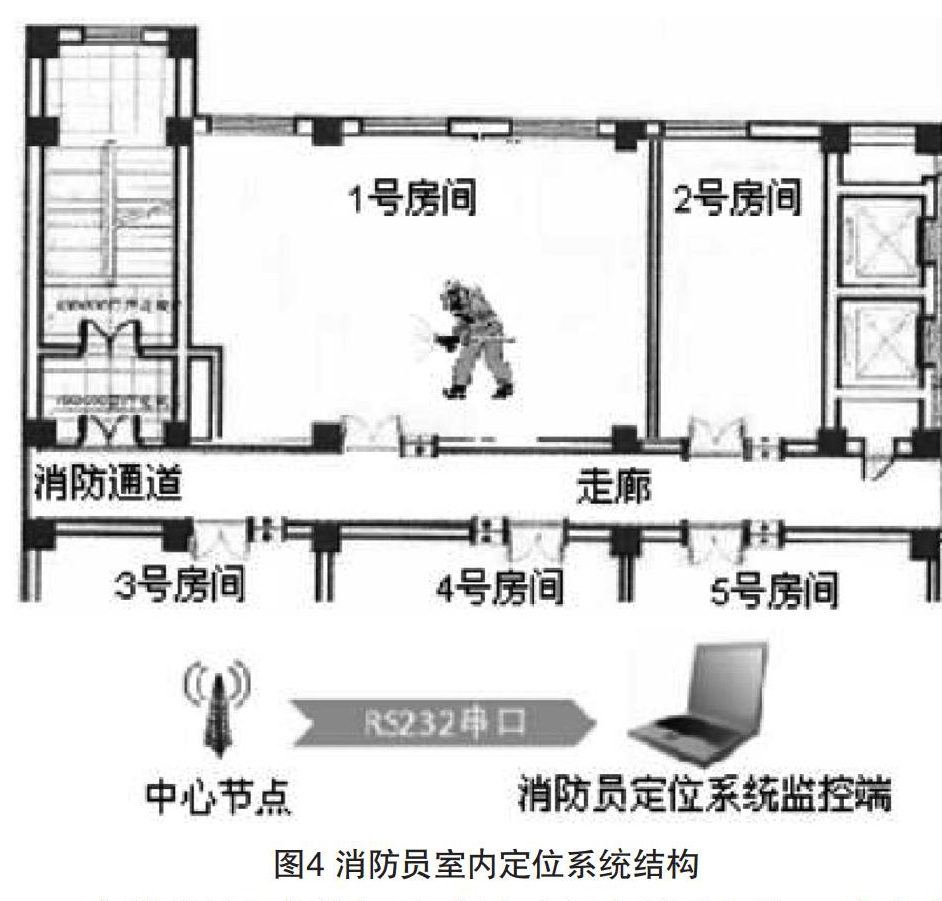
為了验证提出的无线定位算法及定位系统的实际应用效果,在本市消防中队与某公司联合举办的消防演习中,消防员配备基于CC2500芯片的定位设备后,进入已布置参考结点的办公楼内对被困人员进行搜救及疏散。基于无线传感器网络的消防员室内定位系统结构如图4所示,其中黑色方块为布置的参考节点,可以对消防员携带的接收设备发射RSSI信号。接收设备接收到多个RSSI信号后使用算法进行定位坐标计算,并将定位结果通过无线信号发送给中心节点,中心节点再将消防员的位置等信息发送至消防员定位系统监控端,指挥中心可以在监控端屏幕上实时掌握消防员的位置等信息,再进行统一指挥部署。
实验背景和参数如下:每个房间内需要布置4~8个参考节点,参考节点的具体数量视房间大小而定,走廊以5米间隔布置参考节点,办公楼内的走廊及房间内均有桌椅、电脑、柜子等物品。大厅较为空旷,可以将参考节点布置的间隔设为8~12米。中心节点布置在指挥中心,使用串口线与消防员室内定位系统监控端进行连接。在消防员随身携带的定位设备中,将遗传算法中的各参数进行如下设置:初始种群数量为30,交叉概率为0.5,变异概率为0.02。算法并未设置指定的遗传代数,而是限定算法运行的总时间为300 ms,同时将定位频率设为500 ms,为系统保留了200 ms的休眠时间,以达到节省设备电能、延长设备使用时间的目的。上述参数均可以在指挥中心的监控端软件实时进行远程设置。
为了与改进的极大似然估计定位算法进行定位精度的比较,先通过监控端的远程参数设置功能,将消防员随身携带的定位设备中的定位算法设为改进的极大似然估计定位算法,运行15分钟后,再将定位算法设为改进的遗传算法,并运行相同的时间。消防员随身携带的定位设备将每次计算出的定位结果发送给中心节点,中心节点再将每次的定位结果通过RS232串口发送给指挥中心监控端,监控端将遗传算法与改进的极大似然估计定位算法运行的结果各取平均值后进行数据对比,结果如表1和图5所示。
从实验结果可以看出,在与参考节点的最近距离为2~12米范围内时,基于遗传算法的定位算法比改进的极大似然定位算法的平均定位误差降低了约10% ~ 30%,有效地提高了定位精度。其中在4米处左右,因障碍物较多造成了在该点处的RSSI信号波动较为明显,使用改进的算法后平均定位误差仍比改进的极大似然定位算法降低了约20.55%。
5 结语
本文针对典型的极大似然定位算法、质心定位算法及改进的相关算法的不足之处进行了分析,文章提出了基于遗传算法的定位算法。该算法采用考虑参考节点RSSI信号波动误差的质心算法进行种群初始化,充分考虑了参考节点的测距可信度。在参考节点的测距误差区域内部与外部使用不同的适应度函数进行度量,既可以增加搜索初期的搜索范围,又可以在搜索后期进行更精确的优化。结合基于记忆搜索方向的交叉机制和自适应调整搜索半径的策略,为下一代种群的搜索方向及搜索半径提供了指导信息,有效地提高了种群进化的速度并提高了定位精度。
[参考文献]
[1]MUNOZ D, BOUCHEREAU F, VARGAS C, et al.Position location techniques and applications[M]. Burlington:Academic Press, 2009.
[2]MERAT S, ALMUHTADI W. Wireless network channel quality estimation inside reactor building using RSSI measurement of wireless sensor network[A].Proceeding in Electrical and Computer Engineering, 2009[C]. Canada:Canadian Conference on Electrical and Computer Engineering, 2009:339-341.
[3]WASSI G I, DESPINS C, GRENIER D, et al. Indoor location using received signal strength of IEEE 802.11b access point[C]. Canada:Canadian Conference Electrical and Computer Engineering, 2005:1371-1374.
[4]CHEN P C. A non-line-of-sight error mitigation algorithm in location estimation[J].IEEE Wireless Communication and Network, 1999(1):316-320.
[5]WYLIE M P, HOLTZMAN J. The non-line of sight problem in mobile location estimation[C].Boston:5th IEEE International Conference on Universal Personal Communications, 1996:827-831.
[6]陈维克,李文锋,首珩,等. 基于RSSI的无线传感器网络加权质心定位算法[J]. 武汉理工大学学报,2006(2):265-268.
[7]WEIKE C, WENFENG L, HENG S, et al. Weighted centroid localization algorithm based on RSSI for wireless sensor networks[J]. Journal of WuHan University of Technology, 2006(2):265-268.
[8]石琴琴,霍宏,方涛,等.使用最速下降算法提高极大似然估计算法的节点定位精度[J].计算机应用研究,2008(7):2038-2040.
[9]QINQIN S, HONG H, TAO F, et al. Using steepest descent method to improve node localization[J]. Application Research of Computers, 2008(7):2038-2040.
[9]MICHALEWICZ Z, JANIKOW C Z, KRAWCZYK J B. A modified genetic algorithm for optimal control problems[J]. Computers and Mathematics with Applications, 1992(12):83-94.
[10]GREFENSTELLE J J, GOPAL R, ROSMAITA B, et al. Genetic algorithms for the traveling salesman[C]. USA:Proceeding of International Conference of genetic algorithm and their applications, 1985(7):359-371.
[11]KUSHKI A, PLATANIOTIS K, VENETSANOPOULOS A.Intelligent dynamic radio tracking in indoor wireless local area networks[J]. IEEE Transactions on Mobile Computing, 2010(3):405-419.

