巧用转化策略提升解题能力

    杨昆

    

    

    

    摘要：小学数学涉及很多图形知识，其中求解图形面积、线段长度是重要考點。部分问题具有一定难度，不仅需要学生牢固掌握基础知识，而且需要具备灵活的思维，需要根据给出的已知条件进行巧妙的转化。为让学生掌握转化技巧，提升图形问题的解题能力，教学中应做好题型的总结，为学生逐一的剖析，为他们解答相关习题带来启发。

    关键词：小学数学 图形问题 解题能力

    小学数学中涉及的图形有三角形、平行四边形、梯形、圆形以及长方体、正方体、圆柱体、圆锥体等，相关题型复杂多变，学生仅仅掌握基础知识是不够的，还应注重学习相关的解题方法与技巧，充分挖掘题干中的隐含条件并进行巧妙的转化，才能实现顺利求解。因此，教学中，教师应结合具体例题，为学生讲解转化的相关技巧，促进其解题水平的提升。

    一、用割补法解答图形问题

    割补法是解决图形问题的重要方法之一，具有较强的灵活性，需要根据已知条件对分开的、看似无规则的图形进行割补，将之转化为规则的、易于求解的图形。教学中，教师应为学生讲解割补法的相关知识，加深其对该种方法的认识与理解，提高其应用割补法解答图形问题的意识。同时，为让学生掌握割补法在解题中的应用，教师应筛选具有代表性例题，与学生一起分析解题思路，使学生在加深印象的同时掌握割补法适宜解答的题型、积累割补法应用经验，以便再遇到类似问题时能够及时找到解题突破口，实现快速、高效解题。

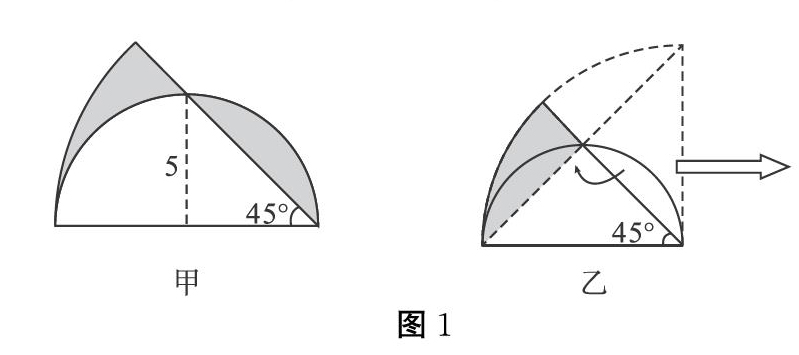
    例1，已知半圆的半径为5厘米，已知角度已在图1（甲）中标出，求图中阴影部分的面积（π取3.14）。

    分析：图1（甲）中的阴影部分是分开的，而且不规则，看似无法直接运用所学知识求解。事实上，可以将右侧的阴影部分割补到左侧与之对应的位置，然后运用扇形及三角形面积计算公式，通过作差求解。

    解答：运用割补法将图1（甲）转化为图1（乙）。由于半圆的半径为5厘米，因此直径为10厘米，对应扇形的半径也为10厘米。由图中45°角可知，扇形的面积为半径10厘米圆的1[]8，对应圆的面积S圆=10×10×π=100π平方厘米，对应扇形的面积为S扇=1[]8×100π=12.5π平方厘米，而空白三角形的面积S三角形=1[]2×10×5=25平方厘米。综上可知，阴影部分的面积S阴影=12.5×3.14-25=14.25平方厘米。

    二、用平移法解答图形问题

    平移法是通过平移一些图形，将原本看似复杂的图形转化为规则图形的一种解题方法。通过平移，能降低分析问题的难度，提高解题的成功率。教学中，为让学生掌握平移法，一方面，教师应讲解使用平移法解答的例题，帮助学生弄清平移的思路。另一方面，应鼓励学生总结适宜平移法解题的题型，尤其对于被分隔成多个部分的图形，可考虑使用平移法进行转化、解题。另外，应鼓励学生积极思考，总结使用平移法解题的技巧，即根据题目要求，平移图形时可将图形适当变形，如在保持图形面积不变的基础上可将平行四边形变形为长方形，从而降低计算复杂度。

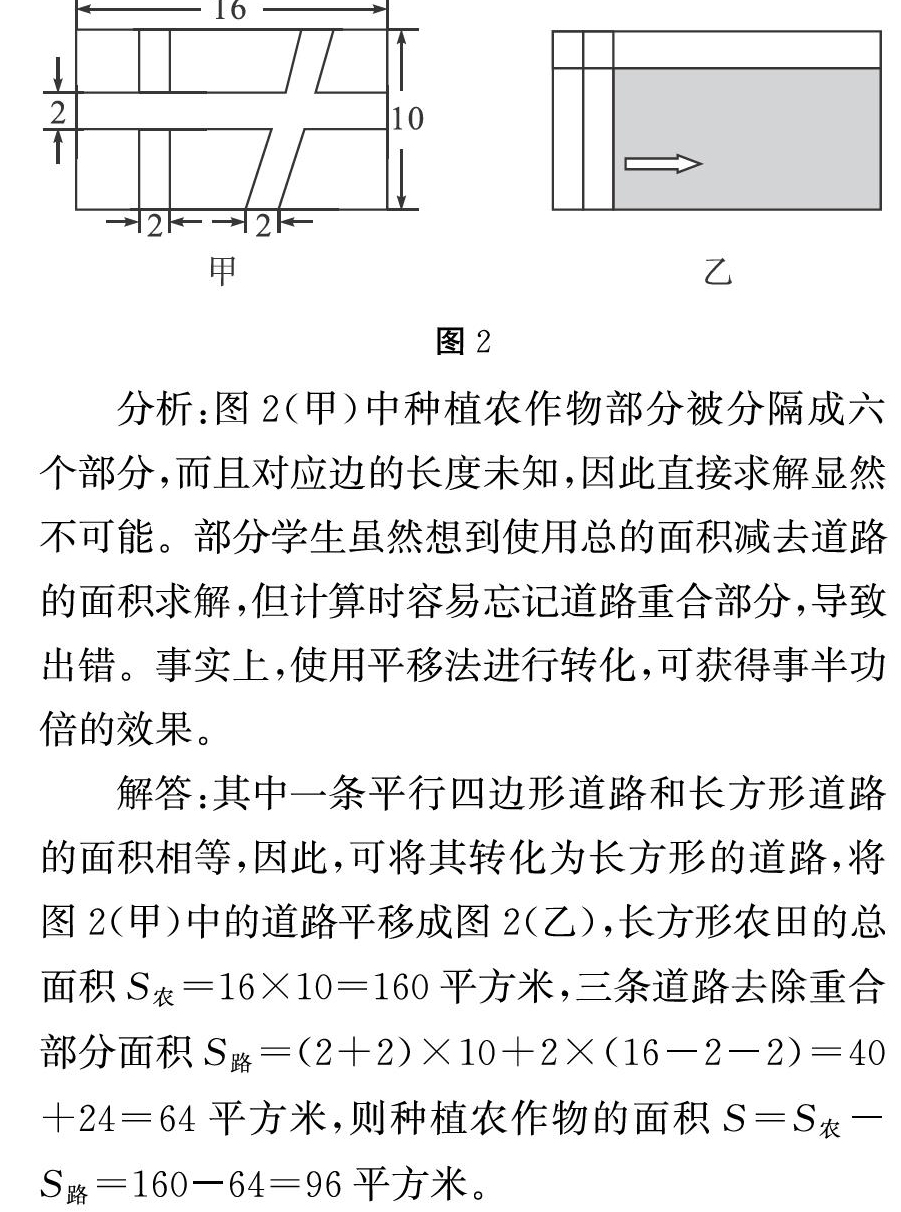
    例2，如图2（甲）为一块长16米、宽10米的长方形农田，中间分布两条长方形、一条平行四边形的道路，道路的宽均为2米。则该农田种植农作物的面积有多大？

    分析：图2（甲）中种植农作物部分被分隔成六个部分，而且对应边的长度未知，因此直接求解显然不可能。部分学生虽然想到使用总的面积减去道路的面积求解，但计算时容易忘记道路重合部分，导致出错。事实上，使用平移法进行转化，可获得事半功倍的效果。

    解答：其中一条平行四边形道路和长方形道路的面积相等，因此，可将其转化为长方形的道路，将图2（甲）中的道路平移成图2（乙），长方形农田的总面积S农=16×10=160平方米，三条道路去除重合部分面积S路=（2+2）×10+2×（16-2-2）=40+24=64平方米，则种植农作物的面积S=S农-S路=160-64=96平方米。

    三、用转换法解答图形问题

    转换法是一种间接求解图形问题的方法。当采用直接法求解图形问题的难度较大时，可转换为求解问题的反面，得出反面的结果后，用总体减去反面，便可得出要求解的结果。为使学生熟练应用转换法解答图形问题，教学中，教师应展示相关例题，引导学生从整体上把握图形，不要只盯着要求解的问题，通过转换寻找解决问题的思路。另外，要让学生多加练习，在训练中积累转换法的应用技巧，鼓励学生多与同学沟通、交流，注重借鉴他人优点，不断提升自己的解题水平。

    例3，如图3，长方形ABCD的长和宽分别为5厘米、3厘米，EF将其分成两个长方形，在边AB和CD上分布着大小不等的三角形，其顶点均落在EF上，求空白部分的面积。

    分析：题目给出的已知条件非常少，对多数学生而言直接求解空白部分的面积难度较大。解题时可采用转换法，通过求解阴影部分的面积间接的求出空白部分的面积。

    解答：长方形ABCD的面积S长=5×3=15平方厘米。求解阴影部分面积时可先分析三角形面积的表达式，从中找到规律，而后进行解答。以长方形ABFE中的三角形为研究对象，其面积表达式均为1[]2×底×高。高均相等，等于BF的长，而各底加起来正好为AB的长，则其总面积为S1=1[]2×AB×BF。同理，在长方形EFCD中也存在这一规律，其总面积S2=1[]2×CD×FC，而AB=CD=5厘米，BF+FC=3厘米，则S1+S2=1[]2×AB×BC，表明其为长方形ABCD面积的一半，则空白部分的面积S=1[]2S长=7.5平方厘米。

    四、用代换法解答图形问题

    代换法主要运用的是面积或线段相等，通过等量代换实现解题的一种方法，在解答小学数学图形问题中应用率较高。为让学生掌握这一重要方法，对题干进行巧妙的转化，实现快速解题，教学中教师应引导学生关注图形中的等量关系，如在长方形中两条长和两条宽分别相等、正方形中四条边均相等。同时，设计针对性的问题，与学生一起分析、解答，使其深入理解代换法的具体应用。

    例4，如图4，ADHE为长方形，BCGF为正方形，其中正方形两条边和长方形AD、EH边重合，其中FH=18厘米，AC=24厘米，求长方形ADHE的周长。

    分析：题目中并未直接给出长方形ADHE的长和宽，需要从已知条件中找到等量关系，通过替换解答长方形ADHE的周长。

    解答：由已知条件可知FH=18，AC=24厘米，即，FG+GH=18厘米，AB+BC=24厘米。则AC+FH=AB+BC+FG+GH=42厘米。又因为GH=CD，根据所学的长方形、正方形边的等量关系可知，BC=FG=HD。则AC+FH=AB+BC+CD+HD，而AB+BC+CD=AD，因此，AC+FH=AD+HD，因此，长方形ADHE的周长=2×（AC+FH）=2×42=84厘米。

    小学数学图形问题教学中，为提高学生的解题能力，应让学生认识到转化的重要性，尤其要结合经典例题讲解不同题型地转化方法，包括割补、平移、转换、代换等，让学生掌握这些转化方法的应用技巧以及注意事项，提高其灵活应用转化思想解决问题的能力。

    参考文献：

    [1]徐大莲.小学数学高年级“图形与几何”错题类型分析及对策研究[J].学周刊，2020（3）：20.

    [2]叶品贤.基于数形结合思想的小学数学图形与几何教学研究[J].科学咨询（教育科研），2019（9）：166.

    [3]蒋敏杰.小学数学“图形认识”教学的目标立意与实施策略[J].中小学教学研究，2019（2）：8-14.