2009年中考概率命题趋势分析
概率作为新课标新增加的内容,在近年中考试题中越来越得到重视,有些省市甚至将概率问题设计成压轴题,分值在12分左右;对概率知识的考查也从简单的概率计算到更关注对概率意义的理解,建立简单的概率模型,分析解决实际问题等.
1 概率命题趋势分析
1.1 对概率意义的理解及概念的考查
ダ1 一只不透明的布袋中有十只小球(除颜色以外没有任何区别),分别是2个红球,3个白球和5个黑球,每次只摸出一只小球,观察后放回搅匀.在连续9次摸出的都是黑球的情况下,第10次摸出红球的概率是______.
シ治 因为每次摸球都是独立的,且属于摸后放回等可能的模型,相对于每一次摸球而言,其概率都是相同的,该事件可能发生的次数与总次数的比就是所求的概率.
解答:1/5.
评注 本题以摸球背景来设计问题,着重考查学生对概率意义的“等可能”和“独立性”的理解.
例2 (泰州?2008)有下列事件:①367人中必有2人的生日相同;②抛掷一只均匀的骰子两次,朝上一面的点数之和一定大于等于2;③在标准大气压下,温度低于0℃时冰融化;④如果a、b为实数,那么a+b=b+a.其中是必然事件的有()
A.1个B.2个C.3个D.4个
分析在一定条件下必然要发生的事件是必然事件;在一定条件下可能发生也可能不发生的事件是随机事件.
解答:C.
评注 本题考查了必然事件与随机事件的区别.
1.2 对等可能事件概率的考查
例3 (连云港?2008)甲、乙两人玩“锤子、石头、剪子、布”游戏,他们在不透明的袋子中放入形状、大小均相同的15张卡片,其中写有“锤子”、“石头”、“剪子”、“布”的卡片张数分别为2,3,4,6.两人各随机摸出一张卡片(先摸者不放回)来比胜负,并约定:“锤子”胜“石头”和“剪子”,“石头”胜“剪子”,“剪子”胜“布”,“布”胜“锤子”和“石头”,同种卡片不分胜负.
(1)若甲先摸,则他摸出“石头”的概率是多少?
(2)若甲先摸出了“石头”,则乙获胜的概率是多少?
(3)若甲先摸,则他先摸出哪种卡片获胜的可能性最大?
分析 本题解法多样,可以用树状图,也可以用列表.
略解 (1)1/5;(2)4/7;(3)甲先摸出“锤子”获胜的可能性最大.
评注 本题采用了以游戏作为试题背景,重在考查学生对概率模型的理解以及对事件发生概率值的计算.
1.3 对频率与概率之间关系的考查
例4 (贵阳?2008)在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
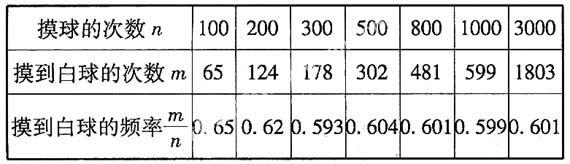
(1)请估计:当n很大时,摸到白球的频率将会接近______.(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(白球)=______.
(3)试估算盒子里黑、白两种颜色的球各有多少只?
分析 相同条件下进行多次重复试验,某一事件发生的概率稳定于事件发生的频率.
略解 (1)0.6;(2)3/5;(3)黑球16只、白球24只.
评注 本题以游戏作为试题背景,让学生经历问题情境——实验探究的过程,重在考查学生对实验频率稳定于理论概率的理解与应用.
1.4 突出概率与现实生活的联系
例5 (宜宾?2008)5月11日是“母亲节”,《×××时报》在2008年5月8日刊登了一则有奖征集活动启事:2008年5月8日起至2008年5月11日止,你可以通过拨打爱心热线电话、发送爱心短信和登陆社区文明网站三种方式参加“爱的感言”和“爱的祝福”活动,活动规则如下:
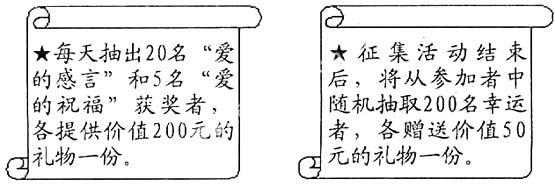
请你利用这则启事中的相关信息解决下列问题:
(1)活动主办方在这次活动中要准备的礼物总价值是多少元?
(2)若预计每天参与活动的人数是2000人,其中你也发送了一条短信,那么,请你算一算自己成为200元和50元礼物获得者的概率分别是多少?
略解 (1)30000元;(2)1/80,1/40.
评注 本题考查了学生应用概率知识分析解决实际问题的能力.
1.5 概率与其它知识相结合
例6 (芜湖?2007)阅读以下材料,并解答以下问题.
“完成一件事有两类不同的方案,在第一类方案中有m种不同的方法,在第二类方案中有n种不同的方法.那么完成这件事共有N= m + n种不同的方法,这是分类加法计数原理;完成一件事需要两个步骤,做第一步有m种不同的方法,做第二步有n种不同的方法.那么完成这件事共有N=m×n种不同的方法, 这就是分步乘法计数原理.”如完成沿图1所示的街道从A点出发向B点行进这件事(规定必须向北走,或向东走),会有多种不同的走法,其中从A点出发到某些交叉点的走法数已在图2填出.
(1) 根据以上原理和图2的提示,算出从A出发到达其余交叉点的走法数,将数字填入图2的空圆中,并回答从A点出发到B点的走法共有多少种?
(2) 运用适当的原理和方法算出从A点出发到达B点,并禁止通过交叉点C的走法有多少种?
(3) 现由于交叉点C道路施工,禁止通行. 求如任选一种走法,从A点出发能顺利开车到达B点(无返回)概率是多少?
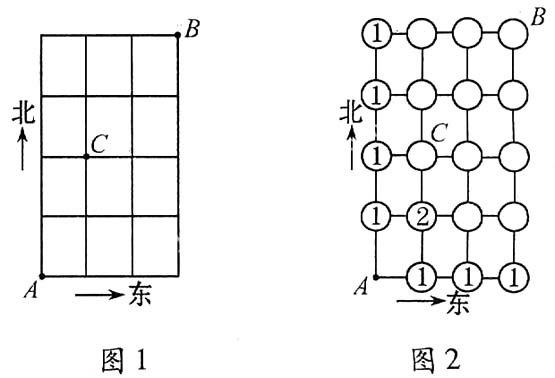
分析 从A点出发到B点必须向北或向东走,使用分类加法计数原理;从A出发经C到B可分两步:先从A到C,再从C到B;可用分类加法计数原理算出从A到C及从C到B的走法,再由分步乘法计数原理求从A出发到达B并禁止通过C的走法.
略解 (1) 填图略,35.(2)17.(3)P(顺利到达B点)=17/35 .
评析 把阅读理解与概率知识结合考查,令人耳目一新,这类试题既能考查学生的自学能力和阅读理解能力,又能考查学生接收、加工和利用信息的能力.
例7 (龙岩?2008)下表为抄录北京奥运会官方票务网公布的三种球类比赛的部分门票价格,某公司购买的门票种类、数量绘制的条形统计图如图3.

ヒ谰萆狭型肌⒈恚回答下列问题:
(1)其中观看男篮比赛的门票有______张;观看乒乓球比赛的门票占全部门票的______%;
(2)公司决定采用随机抽取的方式把门票分配给100名员工,在看不到门票的条件下,每人抽取一张(假设所有的门票形状、大小、质地等完全相同且充分洗匀),问员工小亮抽到足球门票的概率是______;
(3)若购买乒乓球门票的总款数占全部门票总款数的[SX(]1[]8[SX)],试求每张乒乓球门票的价格.
略解 (1)30,20;(2)1/2;(3)500.
评注 将概率与统计知识有机结合考查是2008年中考试题的一大特色.
例8 (安徽?2005)两人要去某风景区游玩,每天某一时段开往该风景区有三辆汽车(票价相同),但是他们不知道这些车的舒适程度,也不知道汽车开过来的顺序,两人采用了不同的乘车方案:
甲无论如何总是上开来的第一辆车,而乙则总是先观察后上车,当第一辆车开过来时,他不上车,而是仔细观察车的舒适状况.如果第二辆车的状况比第一辆好,他就上第二辆车;如果第二辆车不比第一辆好,他就上第三辆车.ト绻把这三辆车的舒适程度分为上、中、下三等,请尝试解决下列问题:
(1)三辆车按出现的先后顺序共有几种不同的可能?
(2)你认为甲、乙两人采用的方案,哪一种方案使自己乘坐上等车的可能性大?为什么?
解析 经仔细读题,发现题中隐含着概率模型.容易想到可用A、B、C分别表示三辆车的舒适程度上、中、下三等,车辆出现的先后顺序可记为:ABC、ACB、BAC、BCA、CAB、CBA,共6种可能,使甲坐上等车的概率是1/3,乙坐上等车的概率是1/2.
评注 本题创设甲、乙两人两种选车方案的生活情境,意在考查学生用概率的观点来分析问题、做出决策;本题回避了对问题解决的思路作出任何暗示,需要学生根据实际问题的分析来发现其中所隐含的数学模型,这是一种考查能力的有效做法.
2 对教与学的启示
1.概率是日常生活中的常见现象,学会用概率的观点、随机观念来观察、分析问题,常能走出凭主观臆想做出决策的误区,因此,学习概率对科学决策、提升数学素养意义很大.同时,概率是一个与确定数学有明显差异的、较难理解的数学概念,因此教学中应多让学生思考、讨论,养成一种理性思维的习惯,遇到问题,不仅凭经验、直觉决策,而应当增加理性的分析与计算.
2.在概率问题中有许多有用的基本模型如摸球、转盘试验、掷骰子、抛硬币等,它就类似于代数中的公式与几何中的基本图形,真正把这些模型理解透了,就容易发现这些模型在实际中的种种表现,就自然提高了运用水平与解决问题的能力,就能够顺利地解决一些实际问题.因此,在教学中必须加强对概率问题中的基本模型的分析与应用. 3.学生在解决一些应用性问题时往往会有这样一种感觉,尽管与解题相联系的数学概念和原理相差无几,但问题所处的情境和背景越具有现实意义、越是自己平时见过但从没有想过的、越是新颖和不熟悉的的问题通常就越难.这个“难”不是难在某个特定的解题技巧,而是难在对现实情境的思考和表征:把问题的现实情境符号化,或者建立一个与之等价的数学模型.在日常教学中要从学生已有生活经验出发,让学生亲身经历将实际问题抽象为数学模型并进行解释与应用的过程,提高对数学问题的“翻译”、“转化”能力.
4.数学教学要联系实际,让学生体会到数学的应用价值,打破纯数学知识教学与生活脱节的现象.概率本身是一门在游戏中产生的学科,因此教师要根据初中生的年龄特征,设计形式多样的概率游戏,引领学生在游戏中形成新认识,学习新概念,获得新知识,充分调动学生学习数学的积极性,在游戏中参与数学活动,在游戏中分析、归纳、合作、思考,领悟数学道理.
プ髡呒蚪:周礼寅,江苏东台人,1974年11月生,中学一级教师.东台市教学能手.主要研究中考试题及课堂教学. 多次获上级表彰,在各级报纸、杂志发表论文多篇.
1 概率命题趋势分析
1.1 对概率意义的理解及概念的考查
ダ1 一只不透明的布袋中有十只小球(除颜色以外没有任何区别),分别是2个红球,3个白球和5个黑球,每次只摸出一只小球,观察后放回搅匀.在连续9次摸出的都是黑球的情况下,第10次摸出红球的概率是______.
シ治 因为每次摸球都是独立的,且属于摸后放回等可能的模型,相对于每一次摸球而言,其概率都是相同的,该事件可能发生的次数与总次数的比就是所求的概率.
解答:1/5.
评注 本题以摸球背景来设计问题,着重考查学生对概率意义的“等可能”和“独立性”的理解.
例2 (泰州?2008)有下列事件:①367人中必有2人的生日相同;②抛掷一只均匀的骰子两次,朝上一面的点数之和一定大于等于2;③在标准大气压下,温度低于0℃时冰融化;④如果a、b为实数,那么a+b=b+a.其中是必然事件的有()
A.1个B.2个C.3个D.4个
分析在一定条件下必然要发生的事件是必然事件;在一定条件下可能发生也可能不发生的事件是随机事件.
解答:C.
评注 本题考查了必然事件与随机事件的区别.
1.2 对等可能事件概率的考查
例3 (连云港?2008)甲、乙两人玩“锤子、石头、剪子、布”游戏,他们在不透明的袋子中放入形状、大小均相同的15张卡片,其中写有“锤子”、“石头”、“剪子”、“布”的卡片张数分别为2,3,4,6.两人各随机摸出一张卡片(先摸者不放回)来比胜负,并约定:“锤子”胜“石头”和“剪子”,“石头”胜“剪子”,“剪子”胜“布”,“布”胜“锤子”和“石头”,同种卡片不分胜负.
(1)若甲先摸,则他摸出“石头”的概率是多少?
(2)若甲先摸出了“石头”,则乙获胜的概率是多少?
(3)若甲先摸,则他先摸出哪种卡片获胜的可能性最大?
分析 本题解法多样,可以用树状图,也可以用列表.
略解 (1)1/5;(2)4/7;(3)甲先摸出“锤子”获胜的可能性最大.
评注 本题采用了以游戏作为试题背景,重在考查学生对概率模型的理解以及对事件发生概率值的计算.
1.3 对频率与概率之间关系的考查
例4 (贵阳?2008)在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:

(1)请估计:当n很大时,摸到白球的频率将会接近______.(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(白球)=______.
(3)试估算盒子里黑、白两种颜色的球各有多少只?
分析 相同条件下进行多次重复试验,某一事件发生的概率稳定于事件发生的频率.
略解 (1)0.6;(2)3/5;(3)黑球16只、白球24只.
评注 本题以游戏作为试题背景,让学生经历问题情境——实验探究的过程,重在考查学生对实验频率稳定于理论概率的理解与应用.
1.4 突出概率与现实生活的联系
例5 (宜宾?2008)5月11日是“母亲节”,《×××时报》在2008年5月8日刊登了一则有奖征集活动启事:2008年5月8日起至2008年5月11日止,你可以通过拨打爱心热线电话、发送爱心短信和登陆社区文明网站三种方式参加“爱的感言”和“爱的祝福”活动,活动规则如下:

请你利用这则启事中的相关信息解决下列问题:
(1)活动主办方在这次活动中要准备的礼物总价值是多少元?
(2)若预计每天参与活动的人数是2000人,其中你也发送了一条短信,那么,请你算一算自己成为200元和50元礼物获得者的概率分别是多少?
略解 (1)30000元;(2)1/80,1/40.
评注 本题考查了学生应用概率知识分析解决实际问题的能力.
1.5 概率与其它知识相结合
例6 (芜湖?2007)阅读以下材料,并解答以下问题.
“完成一件事有两类不同的方案,在第一类方案中有m种不同的方法,在第二类方案中有n种不同的方法.那么完成这件事共有N= m + n种不同的方法,这是分类加法计数原理;完成一件事需要两个步骤,做第一步有m种不同的方法,做第二步有n种不同的方法.那么完成这件事共有N=m×n种不同的方法, 这就是分步乘法计数原理.”如完成沿图1所示的街道从A点出发向B点行进这件事(规定必须向北走,或向东走),会有多种不同的走法,其中从A点出发到某些交叉点的走法数已在图2填出.
(1) 根据以上原理和图2的提示,算出从A出发到达其余交叉点的走法数,将数字填入图2的空圆中,并回答从A点出发到B点的走法共有多少种?
(2) 运用适当的原理和方法算出从A点出发到达B点,并禁止通过交叉点C的走法有多少种?
(3) 现由于交叉点C道路施工,禁止通行. 求如任选一种走法,从A点出发能顺利开车到达B点(无返回)概率是多少?

分析 从A点出发到B点必须向北或向东走,使用分类加法计数原理;从A出发经C到B可分两步:先从A到C,再从C到B;可用分类加法计数原理算出从A到C及从C到B的走法,再由分步乘法计数原理求从A出发到达B并禁止通过C的走法.
略解 (1) 填图略,35.(2)17.(3)P(顺利到达B点)=17/35 .
评析 把阅读理解与概率知识结合考查,令人耳目一新,这类试题既能考查学生的自学能力和阅读理解能力,又能考查学生接收、加工和利用信息的能力.
例7 (龙岩?2008)下表为抄录北京奥运会官方票务网公布的三种球类比赛的部分门票价格,某公司购买的门票种类、数量绘制的条形统计图如图3.

ヒ谰萆狭型肌⒈恚回答下列问题:
(1)其中观看男篮比赛的门票有______张;观看乒乓球比赛的门票占全部门票的______%;
(2)公司决定采用随机抽取的方式把门票分配给100名员工,在看不到门票的条件下,每人抽取一张(假设所有的门票形状、大小、质地等完全相同且充分洗匀),问员工小亮抽到足球门票的概率是______;
(3)若购买乒乓球门票的总款数占全部门票总款数的[SX(]1[]8[SX)],试求每张乒乓球门票的价格.
略解 (1)30,20;(2)1/2;(3)500.
评注 将概率与统计知识有机结合考查是2008年中考试题的一大特色.
例8 (安徽?2005)两人要去某风景区游玩,每天某一时段开往该风景区有三辆汽车(票价相同),但是他们不知道这些车的舒适程度,也不知道汽车开过来的顺序,两人采用了不同的乘车方案:
甲无论如何总是上开来的第一辆车,而乙则总是先观察后上车,当第一辆车开过来时,他不上车,而是仔细观察车的舒适状况.如果第二辆车的状况比第一辆好,他就上第二辆车;如果第二辆车不比第一辆好,他就上第三辆车.ト绻把这三辆车的舒适程度分为上、中、下三等,请尝试解决下列问题:
(1)三辆车按出现的先后顺序共有几种不同的可能?
(2)你认为甲、乙两人采用的方案,哪一种方案使自己乘坐上等车的可能性大?为什么?
解析 经仔细读题,发现题中隐含着概率模型.容易想到可用A、B、C分别表示三辆车的舒适程度上、中、下三等,车辆出现的先后顺序可记为:ABC、ACB、BAC、BCA、CAB、CBA,共6种可能,使甲坐上等车的概率是1/3,乙坐上等车的概率是1/2.
评注 本题创设甲、乙两人两种选车方案的生活情境,意在考查学生用概率的观点来分析问题、做出决策;本题回避了对问题解决的思路作出任何暗示,需要学生根据实际问题的分析来发现其中所隐含的数学模型,这是一种考查能力的有效做法.
2 对教与学的启示
1.概率是日常生活中的常见现象,学会用概率的观点、随机观念来观察、分析问题,常能走出凭主观臆想做出决策的误区,因此,学习概率对科学决策、提升数学素养意义很大.同时,概率是一个与确定数学有明显差异的、较难理解的数学概念,因此教学中应多让学生思考、讨论,养成一种理性思维的习惯,遇到问题,不仅凭经验、直觉决策,而应当增加理性的分析与计算.
2.在概率问题中有许多有用的基本模型如摸球、转盘试验、掷骰子、抛硬币等,它就类似于代数中的公式与几何中的基本图形,真正把这些模型理解透了,就容易发现这些模型在实际中的种种表现,就自然提高了运用水平与解决问题的能力,就能够顺利地解决一些实际问题.因此,在教学中必须加强对概率问题中的基本模型的分析与应用. 3.学生在解决一些应用性问题时往往会有这样一种感觉,尽管与解题相联系的数学概念和原理相差无几,但问题所处的情境和背景越具有现实意义、越是自己平时见过但从没有想过的、越是新颖和不熟悉的的问题通常就越难.这个“难”不是难在某个特定的解题技巧,而是难在对现实情境的思考和表征:把问题的现实情境符号化,或者建立一个与之等价的数学模型.在日常教学中要从学生已有生活经验出发,让学生亲身经历将实际问题抽象为数学模型并进行解释与应用的过程,提高对数学问题的“翻译”、“转化”能力.
4.数学教学要联系实际,让学生体会到数学的应用价值,打破纯数学知识教学与生活脱节的现象.概率本身是一门在游戏中产生的学科,因此教师要根据初中生的年龄特征,设计形式多样的概率游戏,引领学生在游戏中形成新认识,学习新概念,获得新知识,充分调动学生学习数学的积极性,在游戏中参与数学活动,在游戏中分析、归纳、合作、思考,领悟数学道理.
プ髡呒蚪:周礼寅,江苏东台人,1974年11月生,中学一级教师.东台市教学能手.主要研究中考试题及课堂教学. 多次获上级表彰,在各级报纸、杂志发表论文多篇.

