应用模型拓展思维 构建相遇问题知识网络

    徐艳

    

    

    

    摘? 要 通过观摩威海恒山实验学校刘永强老师执教的关于相遇问题的优质课，发现相遇问题成为教学难点，不是因为学生的理解力差，而是教师的教学策略有问题，引发笔者对相遇问题教学策略的再思考。

    关键词 小学数学;相遇问题;数学模型;数形结合;学具

    中图分类号：G623.5? ? 文献标识码：B

    文章编号：1671-489X（2020）03-0070-03

    1 引言

    相遇问题是青岛版小学数学三年级下册第九单元“快捷的物流运输：解决问题”的内容，这一内容一直被公认是应用题教学中的难点。但在观摩威海恒山实验学校刘永强老师执教的关于相遇问题的优质课后，笔者发现导致相遇问题成为教学难点的原因，不是学生的理解力差，而是教师的教学策略有问题。刘老师的教学设计轻易把相遇问题的难点一一化解，引发了笔者对相遇问题教学策略的再思考。

    学生对于相遇问题并不陌生，能从已有的生活经验中通过语言描述、情景演示等方式表述相遇问题的基本特征。但是相遇问题涉及两个物体的运动情况，其中的数量关系比较复杂，学习起来有一定的难度。所以要运用学生已有的知识基础和生活经验进行相遇问题的探究，通过对相遇问题进行探究，形成数学模型，进而分析与解决问题。这部分内容的学习有两个方面的难点：

    1）借助摆学具和画图的方式，直观展示数量关系，让学生明确相遇现象所存在的数量关系，通过直观演示建立数学模型;

    2）通过数量关系及相遇问题的特点，理解其中的要素，即速度、时间、总路程等，建立速度与时间相乘等于总路程的数学模型。

    2 借助具体问题情境，提炼题中关键词，明确相遇问题应具备的特征

    【片段一】

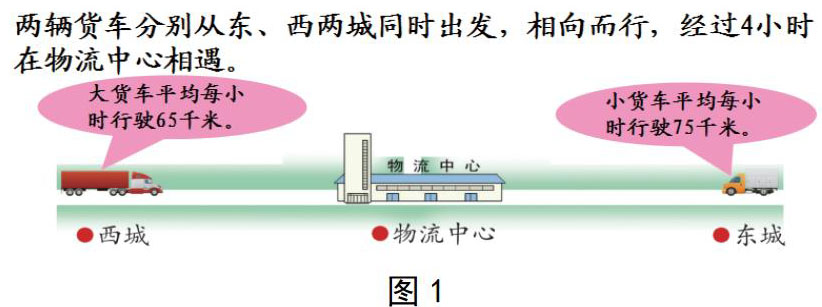
    师：生活中相遇的例子有很多（课件出示图1所示信息），这个问题是不是我们刚才说的相遇问题？

    学生从两个物体、两个地方、相向而行、最终相遇几个方面解释。

    师：那这个相遇问题还告诉了我们什么？

    解释相遇问题的另一特征——同时出发。师生互动演示两辆货车的运动过程。

    师：我们刚才的演示过程还有没有不足的地方？

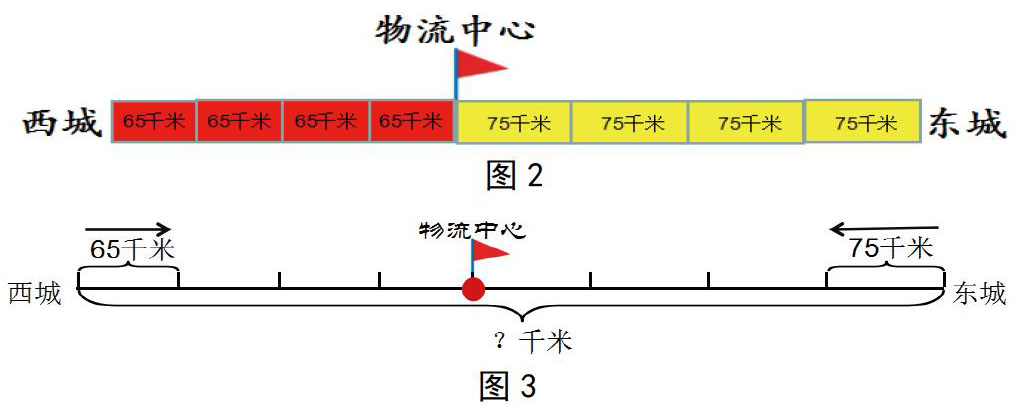
    利用学具演示两辆货车相遇过程，确定相遇点靠近西城（图2）。

    师：看来我们之前模拟的过程确实不够严谨，没有看清具体的数量和它们之间的关系，今后我们要注意全面地考虑问题。

    从课例中看出，刘老师通过一步步追问，让學生更加明确相遇问题应具备的特征——两个物体、两个地方、相向而行、最终相遇;同时在一问一答中引导学生提炼题中的关键词，学会读懂、读透问题。学生在摆学具，理清数量及数量之间的关系中，培养思维严谨的学习品质。

    3 借助线段图，整理信息和问题——构建相遇问题模型

    【片段二】

    师：在解决行程问题的时候，我们经常借助线段图帮助我们整理信息和问题。如果没有学具，我们能不能用画线段图的方式，将信息和问题表示出来呢？

    学生尝试画线段图整理信息和问题——构建相遇问题线段图模型，如图3所示。对错对比，总结画线段图需要注意的地方。

    1）学生独立列式计算，自主解决问题——构建相遇问题的算式模型。

    2）分析比较解法，抽象出数量关系——构建相遇问题的本质模型。

    师：我们一起来回顾一下这两种方法。

    ①学生自主思考，找出解决问题的方法，弄清总路程、时间、速度三者之间的关系，建立计算模型。

    ②分析与比较，弄清相遇问题的特点，抽象出数量关系——构建相遇问题的本质模型。

    师：我们一起来回顾以上解决问题的两个方法。

    课件显示两种解法对比图，如图4所示。

    一种方法是求出大货车与小货车分别在四小时内行驶的路程是多少。因为大货车与小货车是相向而行的，那么四小时内它们相遇，也就是它们行驶的路程正好是总路程，所以说大货车行驶的路程与小货车行驶的路程之和等于总路程。

    另一种方法是先求出大货车与小货车1小时行驶的路程，这里的65是大货车的速度，75是小货车的速度，它们加在一起也就是大货车和小货车的速度和。行驶4小时也就是有4个这样的速度和，因此，速度和×时间=总路程。

    师：下面同桌两人各选择一种方法，对照着线段图向你的同桌说一说先求什么，再求什么。

    经过三个步骤的教学，刘老师引导学生构建出数学模型。

    第一步是直观性探究，让学生通过画图，明确相遇问题的特点、数量关系，初步建立数学图形模型，帮助学生积累数学活动经验，感受数形结合的数学方法美。

    第二步是让学生在建立图形模型的基础上，尝试用列式的形式来解决问题，在学生中开展了互动交流，目的是让学生总结算式模型。交流过程中多处设计了质疑环节，在相互质疑解疑的过程中，培养学生敢于探索、敢于质疑、敢于创新的理性精神。

    第三步采取比较与分析的方式，对相遇问题中存在的数量关系进行抽象处理，使学生弄清相遇问题各数量之间的关系，从而构建本质模型，使学生能够把握整体、系统思考，培养学生有理有据说理的良好思维习惯。

    4 应用模型拓展思维，构建相遇问题知识网络

    【片段三】

    基本练习，巩固新知

    师：这道题（图5）是相遇问题吗？为什么？

    师：根据已知的信息，你认为小方和小丽最有可能在A点还是B点相遇？为什么？

    师：先画线段图整理条件和问题，然后列算式解答这个问题。

    学生在答题纸上做，并集体订正。

    师：看来走路的相遇问题我们也可以用路程1+路程2=总路程和速度和×时间=总路程这两种思路来解决。

    拓展与强化，抓住本质

    师：在日常生活中，车辆有相遇的情况，但是只有车辆有相遇的情况吗？你能举出其他相遇的例子吗？我们一起来看课件（图6）。

    师：能看成相遇问题吗？为什么？

    学生列式解决，全班交流。

    师：生活中还有没有开隧道这样的问题？两个人做什么事情可以看成是相遇问题？

    思维拓展，灵活运用

    师：两个工程队开隧道可以看成相遇问题，那同学们打开思路想一想，生活中两个队或者是两个人一起做了什么别的事情也能看成是相遇问题？

    师：（展示图7）它能不能也看作相遇问题？为什么？

    学生畅言……

    师：刚才两个工程队开隧道、两个人打字，我们都可以看成相遇问题。数学就是这么奇妙，我们只要掌握了相遇问题的特征，就可以拥有一双火眼金睛透过现象看到问题的本质。

    探究交流，构建知识体系

    师：通过本课的学习，大家能不能总结一下，这节课你的主要收获有哪些？

    从三层练习设计的片段可以看出，刘老师的练习设计由浅入深，有坡度，多层次：基本练习引导学生巩固建立的数学模型，实现知识、技能、方法的迁移，促使知识内化;拓展练习引导学生从行程问题拓展到工程问题，沟通知识间的联系，初步尝试用相遇问题模型解释生活中的问题;发展练习，再次引导学生突破固定的思维框架，将录入稿件等更多的问题用相遇问题的模型进行解释应用。引导学生透过现象看本质，学会用数学的眼光观察世界和分析问题，用数学的思维方式分析解决实际问题，用数学的语言表达实际问题;培养学生勇于探索、敢于质疑的理性精神，发展学生的应用意识。

    回顾学习过程的环节，刘老师以具体的问题引领学生从“现实情景—建立模型—运用模型”（图8）进行回顾与整理，让学生互动探讨解决问题的经验，养成善于总结的好习惯，领略数学思想方法的魅力，提高数学核心素养。

    5 结语

    综上所述，相遇问题教学与其他类型应用题教学一样，都要经历分析问题、解决问题、建立模型、运用模型的过程。注重数形结合思想方法的渗透是一种重要的教学策略，在理清相遇问题的多种解題思路中发挥了独特的作用。“教无定法，贵在得法。”广大小学数学教师要做教学研究的有心人，为小学数学教学改革贡献自己的力量。

    参考文献

    [1]罗萍萍.小学数学教学中数学模型的建构策略[J].教书育人，2015（4）：65.

    [2]魏瑞霞.建构数学模型 凸显应用意识[J].基础教育参考，2012（2）：51-53.

    [3]明师.利用数学知识 解决实际问题[J].初中生学习：中考与作文，2008（10）：18-19.