巧用图象分析问题,培养迁移能力
张亚云

物理图象是指借助数学函数的动态变化规律,把物理中需要研究的物理量定位为坐标轴的函数与变量,使两者间的内在关系直观、形象地显现出来,是形象描述物理状态、物理过程和物理规律的常用工具。
一、正确识别图象,激发思维方法
迁移的兴趣
在高中物理功能问题这个章节的学习中,也常用函数图象来描述物理量间的变化规律,如图象、F-s图象、Ek-t图象、EP-x图象、E-x图象、Q-x图象等等。在学习中要正确识别图象、准确把握图象所表达的物理意义,并从图象中获取其中蕴藏的对解题有用信息,从而激发灵活运用图象分析物理问题的方法迁移的兴趣。
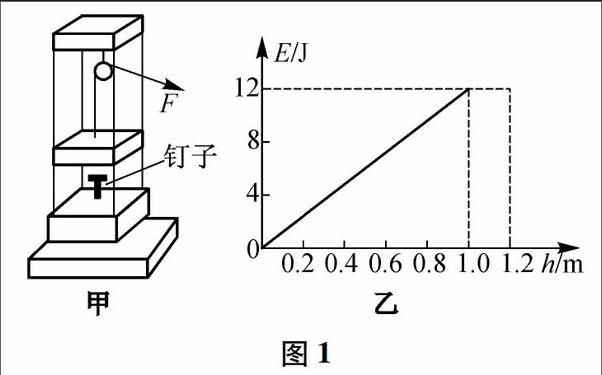
例1 某打桩机的简易模型如图1甲所示。质量m=lkg的物体在拉力F作用下从与钉子接触处由静止开始运动,上升一段高度后撤去F,到最高点后自由下落,最后撞击钉子并将钉子打入一定深度。物体上升过程中,它的机械能与上升高度h的关系图象如图1乙所示。不计所有摩擦,取g=10m/s2.求:
(1)拉力F的大小;
(2)物体上升1m后再经过多长时间才撞击钉子。(结果可保留根号)
(3)物体上升过程中拉力F的最大功率。
仔细观察图1乙,我们首先看到纵轴是机械能E、横轴是物体上升的高度h,且图象从坐标原点开始,马上获得信息:物体在h=0处的机械能为0,则说明此情境中,是以钉子处为零势能参考面。同时,还能获得信息:物体上升A高度时的机械能也是物体增加的机械能。另外,由阁还能直接获得信息,物体上升高度h=1m时,物体的机械能为12J,由此可求得蕴藏的对解题有用信息,即此时物体的速度。
二、学会分析图象,培养思维方法
迁移的意识
图象一般都是描述的两个物理量之间的关系,在正确识别和初步理解图象后,右目巨建立相关的物理情境,充分运用已经学习和掌握的有关物理知识、物理规律列出这两个物理量之间的函数关系式,结合表达式搞清图象所揭示的物理规律或物理量间的函数关系,便能全面系统地看懂图象中的“轴”、“线”、“点”、“斜率”、“面积,,、“截距,,等所表示的物理意义。同时,培养思维方法迁移的意识,遇到图象问题、特别一次函数图象或正比例函数图象的问题时,都可以采用类似方法。
根据机械能守恒的条件可知,若物体上升过程只有重力做功,机械能应当守恒的。但刚才例1中,根据图象知,物体在0?l.0m上升过程中,机械能发生变化,是因为该过程中,除重力做功外,还有拉力做功,且物体增加的机械能E等于拉力F所做的功,即:E=Fh,则图象E—h的斜率k为拉力F的大小。由于该过程中,物体的机械能正比于高度,则说明拉力大小恒定,且F=k=12N,物体做匀加速运动。
物体在1.0m?1.2m上升过程中,机械能E=12J不变,只有重力做功,即物体只受重力作用,刚说明物体上升h=1.0m时,撤去外力。前面已求得撤去F时物体的速度,且方向竖直向上,接下来,物体仅在重力作用下,将做竖直上拋运动。由图可知,刚才在拉力F作用下上升的高度1.0m,则从开始做竖直上拋运动到落到钉子处,物体的位移为-1.0m,根据竖直上拋运动位移公式即可求得时间。
另外,在图象问题中,图线与坐标轴包围的面积在纵轴和横轴代表的量合适时能代表一定的物理意义,即能代表另外某一个物理量,例如功能问题中有图线P-t的面积、F-x图线的面积均表示功。因此,在利用图象分析问题时,有效利用各种图象中的面积可以将复杂问题简化。
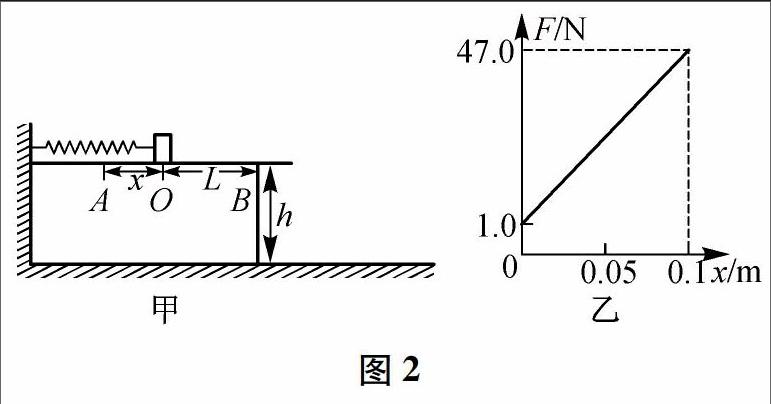
例2 如图2甲所示,一条轻质弹簧左端固定在竖直墙面上,右端放一个可视为质点的小物块,小物块的质量为m=1.0kg,当弹簧处于原长时,小物块静止于0点。现对小物块施加一个外力F,使它缓慢移动,将弹簧压缩至A点,压缩量为x=0.1m,在这一过程中,所用外力F与压缩量的关系如图2乙所示。然后撤去F释放小物块,让小物块沿桌面运动,已知0点至桌边B点的距离为L=2x,水平桌面的高为h=5.0m,计算时,可用滑动摩擦力近似等于最大静摩擦力。(g取10m/s2)求:在压缩弹簧过程中,弹簧存贮的最大弹性势能。
由F-x图象纵轴截距可以获悉,小物块与桌面间的滑动摩擦力大小为Ff=1.0N,在压缩过程中,由于摩擦力是恒力,其做的功可直接根据公式求解。同时,由图象可知,外力F是变力,则不可以直接用公式,但从纵坐标、横坐标的物理单位可看出,该图线与坐标轴包围的面积即为外力F所做的功。则弹簧存贮的弹性势能为
三、努力构造图象,培养思维方法
迁移的习惯
物理规律用数学表达出来后,实质是一个函数关系式,如果这个函数式仅有两个变量,就可用图象来描述物理规律。这样就将代数关系转变为几何关系,而几何关系往往具有直观、形象、简明的特点,可达到化难为易、化繁为简的目的,有利于提高解决物理问题的能力。在物理学习中,要善于运用图象分析问题,培养思维方法迁移的习惯。 例3 如图3所示,有一内壁光滑的闭合椭圆形管道,置于竖直平面内,MN是通过猶圆中心0点的水平线。已知一小球从M点出发,初速率为ν0,沿管道MPN运动,到N点的速率为ν1,所需时间为t1;若该小球仍由M点以初速率ν0出发,而沿管道MQN运动,到N点的速率为ν2,所需时间为t2,则( )
有人遇到这样问题时,看到“光滑”二字,根据机械能守恒定律可知ν1=ν2,再看到两段圆弧长度相同,就不加思考地认为两种情况时间相等。其实,根据小球运动过程中重力做功情况,不难分析,小球由M到P再到N,速率先减小至最小,再增大到原速率。小球由M到Q再到/V,速率先增大至最大,再减小到原速率。由两球运动速率特点以及两条路径的路程相等可画出如图4所示的图象,根据图象就很容易看出小球沿MQN路径运动的平均速率大,所以t1>t2,故选项A正确。
四、善于寻找关系,提升思维迁移的能力
遇到图象问题,特别是一次函数或正比例函数图象时,为了能快速利用截距、斜率等进行正确分析问题,应根据物理情境、物理规律找出两个物理量间的变化关系,寻求两物理量之间的函数关系。而后结合表达式和图象的对应关系列出方程求解题中所有分析的物理量。不行时再进行定性分析,得到两个量之间的正确关系。分析图象问题一定要综合使用各种方法同时进行、灵活处理,提升学生思维迁移的能力。
例4 如图5甲所示,竖直平面内的光滑轨道由倾斜直轨道AB和圆轨道BCD组成,AB和BCD相切于B点,CD连线是圆轨道竖直方向的直径(C、D为圆轨道的最低点和最高点),已知∠BOC=30°。可视为质点的小滑块从轨道上高H处的某点由静止滑下,用力传感器测出小滑块经过圆轨道最高点D时对轨道的压力为F,并得到如图5乙所示的压力F与高度H的关系图象,取g=10m/s2.求:小滑块的质量和圆轨道的半径。
不少学生碰到此题时,受课堂所讲的“F-x图象包围的面积表示F所做的功”的影响,一下子进入思维误区。要注意审题,这里的图象反映的是小滑块经过圆轨道最高点D时对轨道的压力为F,随释放高度H变化的关系图象,且为一次函数图象。因此,课堂教学中,点拨学生根据题中所建立的物理情境,利用动能定理、圆周运动向心力表达式尋找F与H的关系表达式。
解析 设小滑块的质量为m,圆轨道的半径为R
总之,物理图象是数与形结合的产物,是具体与抽象相结合的体现,能够直观地反映物理过程,形象、简洁、生动地展现两个物理量之间的关系,清楚地表达物理过程和物理规律,是分析物理问题的一个重要方法。在解决图象问题时,要注重图象学习,从功能问题的图象分析中,学会将其思维方法运用到其他物理问题的学习之中,培养思维方法迁移能力,从而有力助推高中物理课堂教学系统、快速、协调、长效地延伸、拓展。



物理图象是指借助数学函数的动态变化规律,把物理中需要研究的物理量定位为坐标轴的函数与变量,使两者间的内在关系直观、形象地显现出来,是形象描述物理状态、物理过程和物理规律的常用工具。
一、正确识别图象,激发思维方法
迁移的兴趣
在高中物理功能问题这个章节的学习中,也常用函数图象来描述物理量间的变化规律,如图象、F-s图象、Ek-t图象、EP-x图象、E-x图象、Q-x图象等等。在学习中要正确识别图象、准确把握图象所表达的物理意义,并从图象中获取其中蕴藏的对解题有用信息,从而激发灵活运用图象分析物理问题的方法迁移的兴趣。
例1 某打桩机的简易模型如图1甲所示。质量m=lkg的物体在拉力F作用下从与钉子接触处由静止开始运动,上升一段高度后撤去F,到最高点后自由下落,最后撞击钉子并将钉子打入一定深度。物体上升过程中,它的机械能与上升高度h的关系图象如图1乙所示。不计所有摩擦,取g=10m/s2.求:
(1)拉力F的大小;
(2)物体上升1m后再经过多长时间才撞击钉子。(结果可保留根号)
(3)物体上升过程中拉力F的最大功率。
仔细观察图1乙,我们首先看到纵轴是机械能E、横轴是物体上升的高度h,且图象从坐标原点开始,马上获得信息:物体在h=0处的机械能为0,则说明此情境中,是以钉子处为零势能参考面。同时,还能获得信息:物体上升A高度时的机械能也是物体增加的机械能。另外,由阁还能直接获得信息,物体上升高度h=1m时,物体的机械能为12J,由此可求得蕴藏的对解题有用信息,即此时物体的速度。
二、学会分析图象,培养思维方法
迁移的意识
图象一般都是描述的两个物理量之间的关系,在正确识别和初步理解图象后,右目巨建立相关的物理情境,充分运用已经学习和掌握的有关物理知识、物理规律列出这两个物理量之间的函数关系式,结合表达式搞清图象所揭示的物理规律或物理量间的函数关系,便能全面系统地看懂图象中的“轴”、“线”、“点”、“斜率”、“面积,,、“截距,,等所表示的物理意义。同时,培养思维方法迁移的意识,遇到图象问题、特别一次函数图象或正比例函数图象的问题时,都可以采用类似方法。
根据机械能守恒的条件可知,若物体上升过程只有重力做功,机械能应当守恒的。但刚才例1中,根据图象知,物体在0?l.0m上升过程中,机械能发生变化,是因为该过程中,除重力做功外,还有拉力做功,且物体增加的机械能E等于拉力F所做的功,即:E=Fh,则图象E—h的斜率k为拉力F的大小。由于该过程中,物体的机械能正比于高度,则说明拉力大小恒定,且F=k=12N,物体做匀加速运动。
物体在1.0m?1.2m上升过程中,机械能E=12J不变,只有重力做功,即物体只受重力作用,刚说明物体上升h=1.0m时,撤去外力。前面已求得撤去F时物体的速度,且方向竖直向上,接下来,物体仅在重力作用下,将做竖直上拋运动。由图可知,刚才在拉力F作用下上升的高度1.0m,则从开始做竖直上拋运动到落到钉子处,物体的位移为-1.0m,根据竖直上拋运动位移公式即可求得时间。
另外,在图象问题中,图线与坐标轴包围的面积在纵轴和横轴代表的量合适时能代表一定的物理意义,即能代表另外某一个物理量,例如功能问题中有图线P-t的面积、F-x图线的面积均表示功。因此,在利用图象分析问题时,有效利用各种图象中的面积可以将复杂问题简化。
例2 如图2甲所示,一条轻质弹簧左端固定在竖直墙面上,右端放一个可视为质点的小物块,小物块的质量为m=1.0kg,当弹簧处于原长时,小物块静止于0点。现对小物块施加一个外力F,使它缓慢移动,将弹簧压缩至A点,压缩量为x=0.1m,在这一过程中,所用外力F与压缩量的关系如图2乙所示。然后撤去F释放小物块,让小物块沿桌面运动,已知0点至桌边B点的距离为L=2x,水平桌面的高为h=5.0m,计算时,可用滑动摩擦力近似等于最大静摩擦力。(g取10m/s2)求:在压缩弹簧过程中,弹簧存贮的最大弹性势能。
由F-x图象纵轴截距可以获悉,小物块与桌面间的滑动摩擦力大小为Ff=1.0N,在压缩过程中,由于摩擦力是恒力,其做的功可直接根据公式求解。同时,由图象可知,外力F是变力,则不可以直接用公式,但从纵坐标、横坐标的物理单位可看出,该图线与坐标轴包围的面积即为外力F所做的功。则弹簧存贮的弹性势能为
三、努力构造图象,培养思维方法
迁移的习惯
物理规律用数学表达出来后,实质是一个函数关系式,如果这个函数式仅有两个变量,就可用图象来描述物理规律。这样就将代数关系转变为几何关系,而几何关系往往具有直观、形象、简明的特点,可达到化难为易、化繁为简的目的,有利于提高解决物理问题的能力。在物理学习中,要善于运用图象分析问题,培养思维方法迁移的习惯。 例3 如图3所示,有一内壁光滑的闭合椭圆形管道,置于竖直平面内,MN是通过猶圆中心0点的水平线。已知一小球从M点出发,初速率为ν0,沿管道MPN运动,到N点的速率为ν1,所需时间为t1;若该小球仍由M点以初速率ν0出发,而沿管道MQN运动,到N点的速率为ν2,所需时间为t2,则( )
有人遇到这样问题时,看到“光滑”二字,根据机械能守恒定律可知ν1=ν2,再看到两段圆弧长度相同,就不加思考地认为两种情况时间相等。其实,根据小球运动过程中重力做功情况,不难分析,小球由M到P再到N,速率先减小至最小,再增大到原速率。小球由M到Q再到/V,速率先增大至最大,再减小到原速率。由两球运动速率特点以及两条路径的路程相等可画出如图4所示的图象,根据图象就很容易看出小球沿MQN路径运动的平均速率大,所以t1>t2,故选项A正确。
四、善于寻找关系,提升思维迁移的能力
遇到图象问题,特别是一次函数或正比例函数图象时,为了能快速利用截距、斜率等进行正确分析问题,应根据物理情境、物理规律找出两个物理量间的变化关系,寻求两物理量之间的函数关系。而后结合表达式和图象的对应关系列出方程求解题中所有分析的物理量。不行时再进行定性分析,得到两个量之间的正确关系。分析图象问题一定要综合使用各种方法同时进行、灵活处理,提升学生思维迁移的能力。
例4 如图5甲所示,竖直平面内的光滑轨道由倾斜直轨道AB和圆轨道BCD组成,AB和BCD相切于B点,CD连线是圆轨道竖直方向的直径(C、D为圆轨道的最低点和最高点),已知∠BOC=30°。可视为质点的小滑块从轨道上高H处的某点由静止滑下,用力传感器测出小滑块经过圆轨道最高点D时对轨道的压力为F,并得到如图5乙所示的压力F与高度H的关系图象,取g=10m/s2.求:小滑块的质量和圆轨道的半径。
不少学生碰到此题时,受课堂所讲的“F-x图象包围的面积表示F所做的功”的影响,一下子进入思维误区。要注意审题,这里的图象反映的是小滑块经过圆轨道最高点D时对轨道的压力为F,随释放高度H变化的关系图象,且为一次函数图象。因此,课堂教学中,点拨学生根据题中所建立的物理情境,利用动能定理、圆周运动向心力表达式尋找F与H的关系表达式。
解析 设小滑块的质量为m,圆轨道的半径为R
总之,物理图象是数与形结合的产物,是具体与抽象相结合的体现,能够直观地反映物理过程,形象、简洁、生动地展现两个物理量之间的关系,清楚地表达物理过程和物理规律,是分析物理问题的一个重要方法。在解决图象问题时,要注重图象学习,从功能问题的图象分析中,学会将其思维方法运用到其他物理问题的学习之中,培养思维方法迁移能力,从而有力助推高中物理课堂教学系统、快速、协调、长效地延伸、拓展。

