在一题多解中渗透初中数学核心素养的培养

    苏明海 王兴成

    

    

    

    [摘? 要] 文章对一道经典几何题目证法进行剖析与总结，增强学生对中点问题的理解，并在证法中融入初中数学核心素养的培养，不断提升学生的模型思想与推理能力，切实提升学生的数学学科素养.

    [关键词] 一题多解;初中数学核心素养;几何证明

    《义务教育数学课程标准（2011年版）》（下面简称《课程标准》）是基础教育和课程改革的方向，其明确规定了义务教育阶段的课程目标与考试内容. 《课程标准》中明确要求，数学课应当注重发展学生的数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力和模型思想. 在初中学习阶段，几何证明题能培养学生的几何直观、推理能力和模型思想. 其中，推理主要包含两类：一类是从特殊到一般的推理，主要形式是归纳类比;另一类是从一般到特殊的推理，主要形式是演绎. 剖析经典题目的多种证法，能使学生的图形感更强，能进一步增强学生的结构意识，提升他们的演绎推理能力. 在讲解中对典型结构进行多方向思考，依据已有经验寻找突破口，这是合情推理，能使学生对一类题目的理解更深刻. 提炼结构，形成较强的模型意识，关注几何证明的通性通法，这是培养优秀学生的重要途径.

    ■ 经典题目

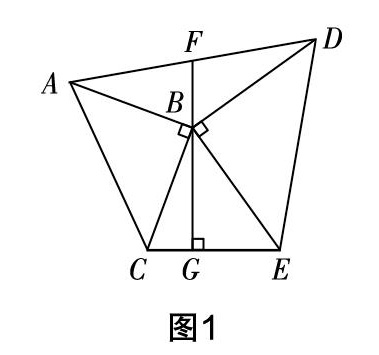
    试题？摇 如图1，△ABC和△BDE都是等腰直角三角形，连接AD，CE，过点B作BG⊥CE，垂足为G，GB的延长线交AD于点F，求证：AF=FD.

    ■

    ■ 结构分析

    对于几何证明题，解题开始时需要具备结构意识与角度意识. 具备结构意识，能快速理清图形结构，对于常规结构，便可快速得到辅助线;具备角度意识，能使学生在初始状态下尽可能地找到隐藏条件，于是可能得到线段相等的结论.

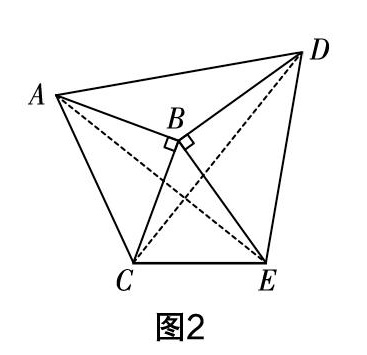
    由已知，图形由两个共直角顶点的等腰直角三角形构成，已构成常见的旋转全等结构，如图2，由此本题可考虑连接AE，CD，构造出△ABE≌△CBD.

    ■

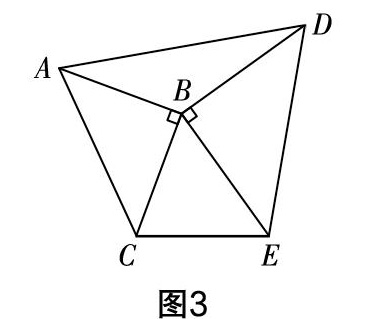
    从角度出发，如图3，∠ABD+∠CBE=180°，这是周角背景下典型的互补结构;如图4，可由三角形外角和定理推得∠ABF=∠BCG. 推导角度时重点考虑这两种结构.

    ■

    由结论，本题要证明两条线段相等，通常可以转化为证明线段所在的两个三角形全等，因此构造全等三角形，所以联系条件证明全等是解题关键. 除此之外，对于中点问题，经常还会考虑中位线、斜中半、三线合一等.

    ■ 题目解析

    1. 推理辅助线，找准基准三角形

    证法1：如图5，过点A作AN∥BD交BF的延长线于点N. 因为AN∥BD，所以∠NAB+∠ABD=180°，∠N=∠NBD. 因为∠ABC=∠EBD=90°，所以∠ABD+∠CBE=180°. 所以∠NAB=∠CBE. 因为BG⊥CE，所以∠BGC=90°. 因为∠BCG+∠BGC=∠CBF，∠ABC=∠BGC=90°，所以∠BCG=∠ABN. 因为△ABC是等腰直角三角形，所以AB=BC. 所以△ABN≌△BCE（ASA）. 所以AN=BE. 因为△BDE是等腰直角三角形，所以BD=BE. 所以AN=BE=BD. 所以△AFN≌△DFB（AAS）. 所以AF=DF.

    ■

    分析？搖 要证明线段相等，优先考虑转化为证明三角形全等，再思考能否利用已知条件或转化已知条件，其目的是为证明全等提供条件. 在本题中，FD所处的基准三角形为△FBD，但AF所处的基准三角形△ABF与△FBD不全等，于是不妨依托△FBD构造全等.

    此法的核心在于转化结论后全等的构造，构造△AFN所需要的辅助线需要选择与对比，而培养学生推理能力的关键也在于此. 一般而言，辅助线应尽可能提供证明全等所需要的条件，其次，构造平行后产生了互补结构，这与已知的互补结构产生联系，从而得到了核心角之间的等量关系. 若选择倍长BF，辅助线就与已知条件无法关联，已知的互补结构就无法给后续全等的证明提供角的等量关系. 教师在讲解时，一定要融入对比，通过推理产生最优的解题路径.

    2. 推理线段角色，巧用旋转背景

    证法2：如图6，延长AB至点M，使得AB=BM，连接DM. 因为∠ABC=∠EBD=90°，所以∠ABD+∠CBE=180°. 因为∠ABD+∠DBM=180°，所以∠DBM=∠CBE. 因为△ABC是等腰直角三角形，所以AB=BC=BM. 因为△BDE是等腰直角三角形，所以BD=BE. 所以△BCE≌△BMD（SAS）. 所以∠BCE=∠M. 因为BG⊥CE，所以∠BGC=90°. 因为∠BCE+∠BGC=∠CBF，∠ABC=∠BGC=90°，所以∠BCE=∠ABF=∠M. 所以BF∥DM. 又AB=BM，所以BF为△AMD的中位线. 所以F为AD的中点，即AF=FD.

    ■

    分析？摇 此证法的核心在于理解线段BF的角色，由结论要证明F是中点，因此BF可理解为中位线. 中位线的构造一定由倍长AB产生，此刻问题转化为证明BF∥DM. 证明平行的本质是证明角相等，即∠ABF=∠M. 由∠BCE=∠ABF，问题转化为证明∠BCE=∠M. 通过角去寻找三角形，可推理出需要证明△BCE≌△BMD. 这是一组旋转全等，旋转中心为点B，由辅助线的构造得两组对边相等，此时可推理出只要证得两组对应边的夹角相等即可. 此处，由两个互补结构完成角相等的证明、全等三角形的证明后，结论得证. 教师在讲解时，一定要深度挖掘结论所包含的隐藏信息，构造以BF为中位线的三角形. 其中，结构意识能帮助学生快速推导角相等，从而完成证明.

    3. 找准核心角以转化问题

    证法3：如图7，在CE上取一点H，使得CH=BF，连接BH. 因为△ABC为等腰直角三角形，所以AB=BC. 因为BG⊥CE，所以∠BGC=90°. 因为∠BCE+∠BGC=∠CBF，∠ABC=∠BGC=90°，所以∠BCE=∠ABF. 所以△ABF≌△BCH（SAS）. 所以AF=BH，∠AFB=∠BHC. 又∠AFB+∠BFD=180°，∠BHC+∠BHE=180°，所以∠BFD=∠BHE. 容易证得∠DBF=∠BEC，又△BDE是等腰直角三角形，所以BD=BE. 所以△BFD≌△EHB（AAS）. 所以BH=FD. 所以AF=FD.

    分析? 此证法的核心在于转移核心线段AF的位置. 由结构分析可得到∠BCE=∠ABF，AB=BC，由此推理出通过构造全等转移AF的位置是可行的. 接下来的辅助线可直接构造出证明全等所需要的第三个条件，此时问题变为证明BH=FD. 同理，可得到BD=BE，∠DBF=∠BEC，这两个等量关系使得BH，FD所处的三角形可能全等，最后由互补结构完成证明. 教师在讲解时，应重点分析转移核心线段AF位置的可能性以及此法最终能够证明的可行性.

    4. 找准核心比例来转化问题

    证法4：如图8，过点F作FQ∥BD交AB于点Q. 因为FQ∥BD，所以∠AFQ=∠ADB，∠AQF=∠ABD，∠QFB=∠FBD. 所以△AQF∽△ABD. 因为BG⊥CE，所以∠BGC=90°. 因为∠BCE+∠BGC=∠CBF，∠ABC=∠BGC=90°，所以∠BCE=∠ABF. 同理，∠FBD=∠BEC，因此∠QFB=∠BEC. 所以△BCE∽△QBF. 因为△BDE和△ABC都是等腰直角三角形，所以BD=BE，AB=BC. 设BD=x，AB=y，QF=a，QB=b，由△AQF∽△ABD，得■=■①，由△BCE∽△QBF，可得■=■②，将②代入①可得y=2b，因此■=■. 又FQ∥BD，所以■=■. 所以AF=FD.

    分析?此证法的核心在于通过平行线转化AF=FD，将线段相等理解为1 ∶ 1. 相似所得的比例式含有4个字母，而最终的结论需要证明AF和AD的2倍关系或AQ与AB的2倍关系，即x与a的数量关系或y与b的数量关系，因此推理出需要利用基本结构进行代数消元. 依托互补结构定位相等角的位置，由此定位△BCE，△BQF，由相似得到等量关系，代入消去x，a后结论得证. 由此法，教师还可将平行线转化比例进行一般化推广.

    基于几何一题多解与核心素养

    培养的思考

    1. 回归基础，强化基本概念，确定解题方向

    几何图形的基本定义、基本性质、基本定理和判定，是学习几何的基础. 对于本题，学生要对等腰直角三角形的基本概念十分清楚，等腰直角三角形可提供角相等与边相等. 从对称性来看，等腰直角三角形是轴对称图形，对称轴是斜边的中垂线;从旋转性来看，在等腰直角三角形BDE中，直角边BD绕直角顶点B顺时针旋转90°后可与BE重合. 一般而言，邊的旋转实则是三角形的旋转. 本题的证法2就可以从旋转的角度来理解，通过旋转做等线段转化. 教师在讲解时，融入这些内容，可使学生对基本几何图形形成一个完整的思维体系. 学生对图形的认识越深刻，解题时的方向感就越强.

    2. 找准核心，提炼基本结构，形成模型意识

    本题的核心在于理解中点，利用中点，转化中点，通过转化中点来转化问题，这是本题的第一个推理点，与中点相关联的基本结构有中位线、倍长中线、三线合一、斜中半. 解题的成功要靠正确思路的选择，要靠从可以接近它的方向去攻击堡垒（G·波利亚语），因此选择构造何种基本结构来解题，依据是能否与已知条件相关联. 本题的第二个推理点是全等或相似的证明，本题中出现的互补结构能够提供角相等，等腰直角三角形可提供边相等，因此可通过等角与等边的位置定位两个三角形，完成全等与相似的证明后即可证明结论.

    对细节结构的推理可精准定位解决问题的方向，从而切实提高学生的解题能力. 因此，教师在讲解时，一定要融入细节结构分析，这是解题方法的指导. 没有对细节结构的理解，解题时学生是盲目的，缺乏方向感. 学生在完成多种解法的梳理时，对中点条件的理解能更加深刻，对基本结构的应用会更加熟练. 我们的目的是让中点问题模型化，让学生以通解通法应对题目万变.

    3. 在过程中提升能力，让能力内化为核心素养

    在学生逻辑推理能力的培养中，几何证明的演绎推理扮演着重要的角色，因此《课程标准》中要求从小学的实验几何要逐步过渡到初中的推理几何. 在几何教学中，教师应引导学生掌握几何基本模型结构，提炼几何证明的通法通性，让学生具备模型意识，从而增强学生的演绎推理能力. 通过对解题方向的归纳与思考，即本题中对中点的理解，能增强学生的合情推理能力.

    几何中一题多解的过程就是合情推理与演绎推理的最好体现，“多”字的内核是合情推理，它提供证明的起点，“解”字的内核是演绎推理，它提供证明的动力，两者相辅相成，辩证统一. 归纳和演绎，正如分析和综合一样，是相互联系着的. 我们不应当牺牲一个而把另一个捧到天上去，应当把每一个都用到该用的地方. 要做到这一点，就只有注意它们的相互联系、它们的相互补充（恩格斯语）. 这里的归纳就是合情推理的一种形式. 因此，在几何教学中，以一题多解为载体，重视学生推理能力的培养，可切实提升学生的学科核心素养.