《曲线运动》之难点巧学
李恒林

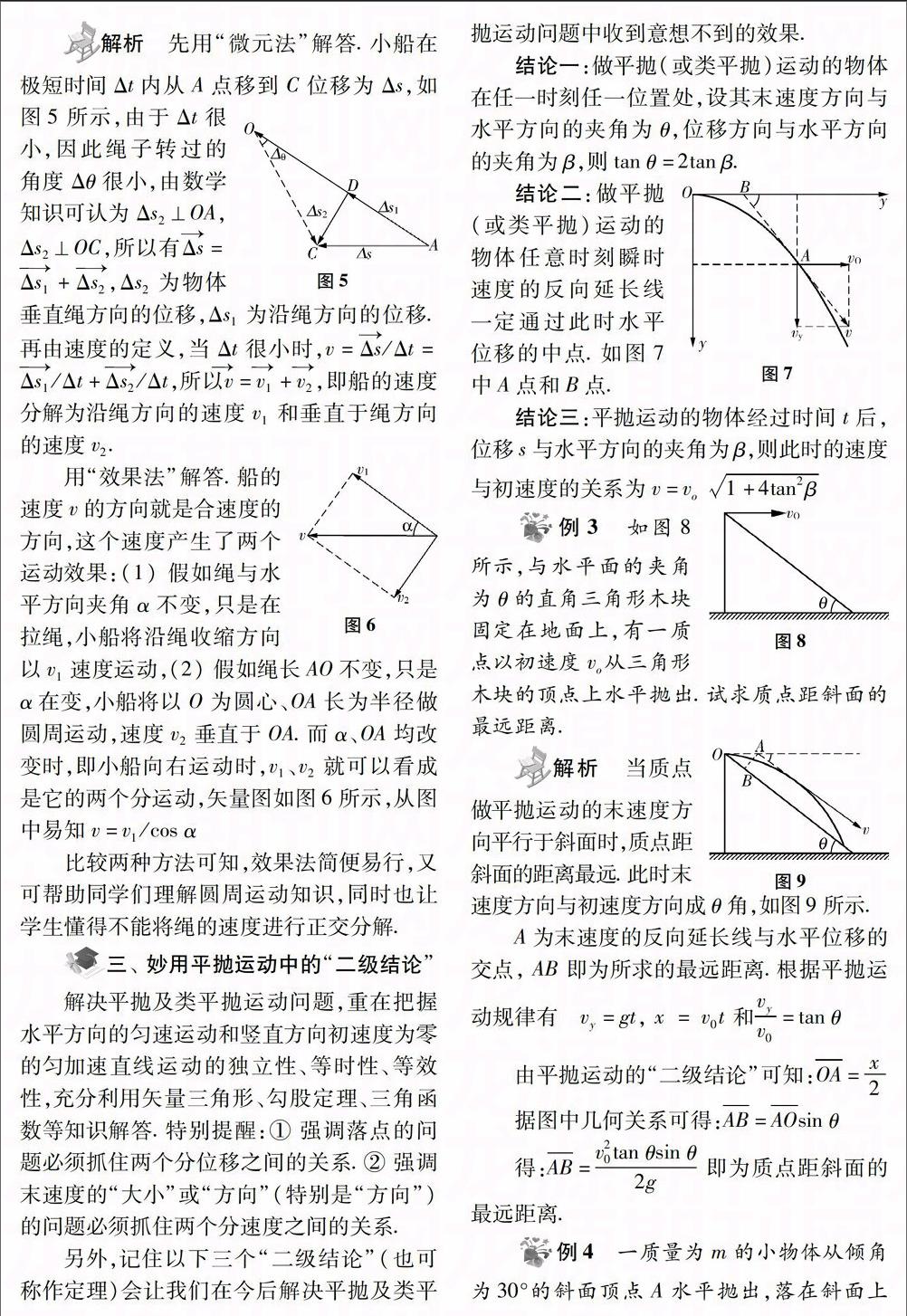

一、巧用“两边夹”确定物体的曲线运动情况
曲线运动是变速运动,从运动学的角度可以确定物体加速度与速度、轨迹之间的关系,也可以从动力学的角度确定合外力F与速度、轨迹之间的关系.
物体做曲线运动的轨迹不外乎以下三种情况:物体的加速度a与其速度υ之间的夹角为锐角、直角或钝角.所谓“两边夹”就是加速度(或合外力)与速度把轨迹夹在中间,即:物体做曲线运动的轨迹总在a与υ两方向的夹角中,且和υ的方向相切,向加速度一侧弯曲.如图1所示中的三种情况.
例1 一质点在某恒力F作用下做曲线运动,图2中的曲线AB是该质点运动轨迹的一段,质点经过A、B两点时的速率分别为υA、υB.
(1)用作图法找出该恒力方向的可能范围.
(2)该恒力的方向能否在过A点或B点的切线上?
(3)该质点从4点到B点的过程中其速度大小如何变化?
(4)若速率有变化,且υA=υB,则速率最大或最小时在什么位置?
解析(1)过A、B两点分别作曲线的切线①和③、法线②和④,如图3所示,从4点看,恒力F应在①线的右侧;从B点看F应在③线的左侧;因恒力的方向是不变的,故应同时满足上述两条件.若平移③线过A点,则①、③两线之间箭头所指的区域即为F在A点的方向可能的范围.
(2)若F在①线上,则它与υA在同一直线上,由于F为恒力,故质点不可能再做曲线运动,这说明F不可能在①线上.若F在③线上,则在A点时υA在垂直于F的方向上有分量,而到B点时垂直于③线的运动分量没有了,这与该方向上没有F分量相矛盾,故F不可能在③线上.
(3)由于F在A点时与υA夹角大于90。,而在B点时与υB夹角小于90。,故质点的速率应该是先减小后增大.
(4)由于已经判定速率为先减小后增大,且υA=υB,则运动过程中速率有最小值,且发生在F与υ垂直的位置.
二、效果法——运动的合成与分解的法宝
力的分解如果不考虑该力产生的效果,对求解往往影响不大,但运动的分解如果不考虑实际效果,就有可能得出错误的结论.反之,若根据运动效果进行分解,会有意想不到的收获.下面以一个曲线运动中常见的题型——“绳连物”模型为例进行说明,
例2如图4所示,用绳牵引小船靠岸,收绳的速度为υ1,在绳子与水平方向夹角为α的时刻,船的速度υ有多大?
解析先用“微元法”解答.小船在
极短时间At内从A点移到C位移为△s,如图5所示,由于△t很小,因此绳子转过的角度△β很小,由数学知识可认为△s2⊥OA,△s2⊥OC,所以有△s=△s1+△s2,△s2为物体垂直绳方向的位移,△s.为沿绳方向的位移.再由速度的定义,当△t很小时,υ=△s/△t=△s1/△t+△s2/△t,所以υ=υ1+υ2,即船的速度分解为沿绳方向的速度υ1和垂直于绳方向的速度υ2.
用“效果法”解答.船的速度υ的方向就是合速度的方向,这个速度产生了两个运动效果:(1)假如绳与水平方向夹角α不变,只是在拉绳,小船将沿绳收缩方向以υ1速度运动,(2)假如绳长AO不变,只是α在变,小船将以O为圆心、OA长为半径做圆周运动,速度υ2垂直于OA而α、OA均改变时,即小船向右运动时,υ1、υ2就可以看成是它的两个分运动,矢量图如图6所示,从图中易知υ = υ1/cos α
比较两种方法可知,效果法简便易行,又可帮助同学们理解网周运动知识,同时也让学生懂得不能将绳的速度进行正交分解.
三、妙用平抛运动中的“二级结论”
解决平抛及类平抛运动问题,重在把握水平方向的匀速运动和竖直方向初速度为零的匀加速直线运动的独立性、等时性、等效性,充分利用矢量三角形、勾股定理、三角函数等知识解答.特别提醒:①强调落点的问题必须抓住两个分位移之间的关系.②强调末速度的“大小”或“方向”(特别是“方向”)的问题必须抓住两个分速度之间的关系.
另外,记住以下三个“二级结论”(也可称作定理)会让我们在今后解决平抛及类平抛运动问题中收到意想不到的效果.
结论一:做平抛(或类平抛)运动的物体在任一时刻任一位置处,设其末速度方向与水平方向的夹角为θ,位移方向与水平方向的夹角为β,则tanθ=2tanβ.
结论二:做平抛(或类平抛)运动的物体任意时刻瞬时速度的反向延长线一定通过此时水平位移的中点,如图7中A点和B点.
结论三:平抛运动的物体经过时间t后,位移s与水平方向的夹角为β,则此时的速度与初速度的关系为υ=
例3如图8所示,与水平面的夹角为θ的直角三角形木块固定在地面上,有一质点以初速度υ。从三角形木块的顶点上水平抛出.试求质点距斜面的最远距离.
解析 当质点
做平抛运动的末速度方向平行于斜面时,质点距斜面的距离最远.此时末速度方向与初速度方向成θ角,如图9所示.
A为末速度的反向延长线与水平位移的交点,AB即为所求的最远距离.根据平抛运动规律有
由平抛运动的“二级结论”可知:OA=
据图中几何关系可得:AB =AOsin θ
得:AB=
即为质点距斜面的最远距离.
例4一质量为m的小物体从倾角为30。的斜面顶点A水平抛出,落在斜面上碗内壁上做圆周运动的小球,其轨道平面为水平面,网心在轨道网平面上,而不是在球心.
②向心力不是与重力、弹力、摩擦力等并列的“性质力”,而是据效果命名的“效果力”,故在分析做圆周运动的质点受力时,切不可在性质力上再添加一个向心力.
③坐标系的建立:应用牛顿第二定律解答圆周运动问题时,常用正交分解法,其坐标原点是做圆周运动的物体(视为质点)所在的位置,相互垂直的两个坐标轴中,其中一个坐标轴的方向一定沿半径指向圆心.
六、现代科技和社会热点问题——STS问题
这类试题往往利用物理新模型将教材中难度不大、要求不高,但属重点内容的基础知识及与其相关的例题、习题加以有效拼接,演变成各种立意新颖、设计科学的题目,从更高层次上考查学生对所学基础知识的掌握程度和迁移能力、综合能力、创新能力.这类题具有“高起点、低落点”的特点,起点高是指科技成果新,题型新颖、独特,为题海所无法包容;落点低是指完成这些题目所需的基础知识不超纲.
例6 从空间同一点O,同时向各个方向以相同的速率抛出许多小球,不计空气阻力,试证明在这些球都未落地之前,它们在任一时刻的位置可构成一个球面.
解析 假设在O点另有一个小球A,当所有小球被抛出的那一瞬间,让O点处的这个假设小球做自由落体运动.
因为做抛体运动的所有小球与假设做自由落体运动的小球A的加速度都相等(都等于重力加速度),所以,做抛体运动的各小球相对于A球都做匀速直线运动,其位移(注意:是相对于做自由落体运动的小球A的位移)的大小都是.s= vot(v0为各小球抛出时的初速率,t为小球运动的时间),也就是说,在同一时刻,各小球与A的距离都相等,因各小球在同一时刻在空中的位置可构成一个球面,这个球面的半径为R= vot.可见,不同时刻,这些小球的位置构成不同球面,当然,这些球面的球心就是假设做自由落体运动的小球A.
这可解释节日的夜晚燃放的烟花在空中为什么是球形的.
例7 早在19世纪,匈牙利物理学家厄缶就明确指出:“沿水平地面向东运动的物体,其重量,即:列车的视重或列车对水平轨道的压力一定要减轻.”后来,人们常把这类物理现象称之为“厄缶效应”,
我们设想,在地球赤道附近的地平线上,有一列车质量是m,正在以速度v沿水平轨道向东匀速行驶.已知地球的半径R及地球自转周期T.今天我们像厄缶一样,如果仅仅考虑地球自转的影响,火车随地球做线速度为
的圆周运动时,火车对轨道的压力为FN;在此基础上,又考虑到这列火车相对地面附加了一个线速度更快的匀速圆周运动,并设此时火车对轨道的压力为F'N,那么,单纯地由于该火车向东行驶而引起火车对轨道压力减轻的数量FN一F'N为(
)
解析把火车看作一个质点在向东绕地心做匀速圆周运动,向心力由地球对火车的引力F引和地面对火车支持力的合力提供,根据牛顿第二定律得



一、巧用“两边夹”确定物体的曲线运动情况
曲线运动是变速运动,从运动学的角度可以确定物体加速度与速度、轨迹之间的关系,也可以从动力学的角度确定合外力F与速度、轨迹之间的关系.
物体做曲线运动的轨迹不外乎以下三种情况:物体的加速度a与其速度υ之间的夹角为锐角、直角或钝角.所谓“两边夹”就是加速度(或合外力)与速度把轨迹夹在中间,即:物体做曲线运动的轨迹总在a与υ两方向的夹角中,且和υ的方向相切,向加速度一侧弯曲.如图1所示中的三种情况.
例1 一质点在某恒力F作用下做曲线运动,图2中的曲线AB是该质点运动轨迹的一段,质点经过A、B两点时的速率分别为υA、υB.
(1)用作图法找出该恒力方向的可能范围.
(2)该恒力的方向能否在过A点或B点的切线上?
(3)该质点从4点到B点的过程中其速度大小如何变化?
(4)若速率有变化,且υA=υB,则速率最大或最小时在什么位置?
解析(1)过A、B两点分别作曲线的切线①和③、法线②和④,如图3所示,从4点看,恒力F应在①线的右侧;从B点看F应在③线的左侧;因恒力的方向是不变的,故应同时满足上述两条件.若平移③线过A点,则①、③两线之间箭头所指的区域即为F在A点的方向可能的范围.
(2)若F在①线上,则它与υA在同一直线上,由于F为恒力,故质点不可能再做曲线运动,这说明F不可能在①线上.若F在③线上,则在A点时υA在垂直于F的方向上有分量,而到B点时垂直于③线的运动分量没有了,这与该方向上没有F分量相矛盾,故F不可能在③线上.
(3)由于F在A点时与υA夹角大于90。,而在B点时与υB夹角小于90。,故质点的速率应该是先减小后增大.
(4)由于已经判定速率为先减小后增大,且υA=υB,则运动过程中速率有最小值,且发生在F与υ垂直的位置.
二、效果法——运动的合成与分解的法宝
力的分解如果不考虑该力产生的效果,对求解往往影响不大,但运动的分解如果不考虑实际效果,就有可能得出错误的结论.反之,若根据运动效果进行分解,会有意想不到的收获.下面以一个曲线运动中常见的题型——“绳连物”模型为例进行说明,
例2如图4所示,用绳牵引小船靠岸,收绳的速度为υ1,在绳子与水平方向夹角为α的时刻,船的速度υ有多大?
解析先用“微元法”解答.小船在
极短时间At内从A点移到C位移为△s,如图5所示,由于△t很小,因此绳子转过的角度△β很小,由数学知识可认为△s2⊥OA,△s2⊥OC,所以有△s=△s1+△s2,△s2为物体垂直绳方向的位移,△s.为沿绳方向的位移.再由速度的定义,当△t很小时,υ=△s/△t=△s1/△t+△s2/△t,所以υ=υ1+υ2,即船的速度分解为沿绳方向的速度υ1和垂直于绳方向的速度υ2.
用“效果法”解答.船的速度υ的方向就是合速度的方向,这个速度产生了两个运动效果:(1)假如绳与水平方向夹角α不变,只是在拉绳,小船将沿绳收缩方向以υ1速度运动,(2)假如绳长AO不变,只是α在变,小船将以O为圆心、OA长为半径做圆周运动,速度υ2垂直于OA而α、OA均改变时,即小船向右运动时,υ1、υ2就可以看成是它的两个分运动,矢量图如图6所示,从图中易知υ = υ1/cos α
比较两种方法可知,效果法简便易行,又可帮助同学们理解网周运动知识,同时也让学生懂得不能将绳的速度进行正交分解.
三、妙用平抛运动中的“二级结论”
解决平抛及类平抛运动问题,重在把握水平方向的匀速运动和竖直方向初速度为零的匀加速直线运动的独立性、等时性、等效性,充分利用矢量三角形、勾股定理、三角函数等知识解答.特别提醒:①强调落点的问题必须抓住两个分位移之间的关系.②强调末速度的“大小”或“方向”(特别是“方向”)的问题必须抓住两个分速度之间的关系.
另外,记住以下三个“二级结论”(也可称作定理)会让我们在今后解决平抛及类平抛运动问题中收到意想不到的效果.
结论一:做平抛(或类平抛)运动的物体在任一时刻任一位置处,设其末速度方向与水平方向的夹角为θ,位移方向与水平方向的夹角为β,则tanθ=2tanβ.
结论二:做平抛(或类平抛)运动的物体任意时刻瞬时速度的反向延长线一定通过此时水平位移的中点,如图7中A点和B点.
结论三:平抛运动的物体经过时间t后,位移s与水平方向的夹角为β,则此时的速度与初速度的关系为υ=
例3如图8所示,与水平面的夹角为θ的直角三角形木块固定在地面上,有一质点以初速度υ。从三角形木块的顶点上水平抛出.试求质点距斜面的最远距离.
解析 当质点
做平抛运动的末速度方向平行于斜面时,质点距斜面的距离最远.此时末速度方向与初速度方向成θ角,如图9所示.
A为末速度的反向延长线与水平位移的交点,AB即为所求的最远距离.根据平抛运动规律有
由平抛运动的“二级结论”可知:OA=
据图中几何关系可得:AB =AOsin θ
得:AB=
即为质点距斜面的最远距离.
例4一质量为m的小物体从倾角为30。的斜面顶点A水平抛出,落在斜面上碗内壁上做圆周运动的小球,其轨道平面为水平面,网心在轨道网平面上,而不是在球心.
②向心力不是与重力、弹力、摩擦力等并列的“性质力”,而是据效果命名的“效果力”,故在分析做圆周运动的质点受力时,切不可在性质力上再添加一个向心力.
③坐标系的建立:应用牛顿第二定律解答圆周运动问题时,常用正交分解法,其坐标原点是做圆周运动的物体(视为质点)所在的位置,相互垂直的两个坐标轴中,其中一个坐标轴的方向一定沿半径指向圆心.
六、现代科技和社会热点问题——STS问题
这类试题往往利用物理新模型将教材中难度不大、要求不高,但属重点内容的基础知识及与其相关的例题、习题加以有效拼接,演变成各种立意新颖、设计科学的题目,从更高层次上考查学生对所学基础知识的掌握程度和迁移能力、综合能力、创新能力.这类题具有“高起点、低落点”的特点,起点高是指科技成果新,题型新颖、独特,为题海所无法包容;落点低是指完成这些题目所需的基础知识不超纲.
例6 从空间同一点O,同时向各个方向以相同的速率抛出许多小球,不计空气阻力,试证明在这些球都未落地之前,它们在任一时刻的位置可构成一个球面.
解析 假设在O点另有一个小球A,当所有小球被抛出的那一瞬间,让O点处的这个假设小球做自由落体运动.
因为做抛体运动的所有小球与假设做自由落体运动的小球A的加速度都相等(都等于重力加速度),所以,做抛体运动的各小球相对于A球都做匀速直线运动,其位移(注意:是相对于做自由落体运动的小球A的位移)的大小都是.s= vot(v0为各小球抛出时的初速率,t为小球运动的时间),也就是说,在同一时刻,各小球与A的距离都相等,因各小球在同一时刻在空中的位置可构成一个球面,这个球面的半径为R= vot.可见,不同时刻,这些小球的位置构成不同球面,当然,这些球面的球心就是假设做自由落体运动的小球A.
这可解释节日的夜晚燃放的烟花在空中为什么是球形的.
例7 早在19世纪,匈牙利物理学家厄缶就明确指出:“沿水平地面向东运动的物体,其重量,即:列车的视重或列车对水平轨道的压力一定要减轻.”后来,人们常把这类物理现象称之为“厄缶效应”,
我们设想,在地球赤道附近的地平线上,有一列车质量是m,正在以速度v沿水平轨道向东匀速行驶.已知地球的半径R及地球自转周期T.今天我们像厄缶一样,如果仅仅考虑地球自转的影响,火车随地球做线速度为
的圆周运动时,火车对轨道的压力为FN;在此基础上,又考虑到这列火车相对地面附加了一个线速度更快的匀速圆周运动,并设此时火车对轨道的压力为F'N,那么,单纯地由于该火车向东行驶而引起火车对轨道压力减轻的数量FN一F'N为(
)
解析把火车看作一个质点在向东绕地心做匀速圆周运动,向心力由地球对火车的引力F引和地面对火车支持力的合力提供,根据牛顿第二定律得

