把握教学“四点”，知识能力并重

    袁媛

    

    

    

    [摘? 要] 三角形的内角和是三角形的重要性质，其对几何内容的学习极为重要. “三角形的内角和”的课堂教学需要处理好起点、生成点、发展点和提升点四个关键点，文章将结合新课标理念对其加以探究，提出相应的教学建议.

    [关键词] 三角形内角和;理性认知;探究;证明;例题

    “三角形的内角和”是苏教版七年级下册的重要教学内容，该内容探讨的是三角形的一个重要性质，对三角形内角之间的关系有着深刻的揭示，也是后续多边形内角、三角形外角性质和相关角度计算与证明的基础，因此属于基础性极强的内容，下面对其展开教学探讨.

    以学生的认知基础作为教学的

    起点

    教学的起点设定关系到整个教学过程的成功与否，因此应该慎重选取教学起点，帮助学生顺利完成课堂过渡. 一般教师应该以学生的认知水平和已有知识经验作为教学的基础，采用“温故知新”的方式开展课堂引入教学.

    学生在小学阶段通过直观感受已经了解到三角形的内角和为180°，而初中阶段学习的关键是帮助学生完成感性认识到理性认知的过渡，因此使学生掌握演绎推理的思路和方法才是教学的重点. 教师在教学伊始就需要理清几个重要的问题，然后基于问题来设计教学，即学生已经掌握的知识，本节课的教学重点，如何引导学生递进思考.

    而在实际教学中可以采用设问的方式引导学生进行思考，从而联系旧知探索新知，可设置如下问题串.

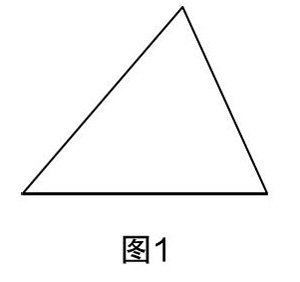
    [图1]

    问题1：图1所示是一个一般的三角形，大家知道它的内角和是多少度吗？

    问题2：大家是如何知道的，可以采用哪些方法说明？

    问题3：大家小组讨论，是否有更为直观的方式来证明？

    在设问引入阶段需要给学生充分的时间，让学生独立思考，交流探讨，充分调动知识经验来探索三角形内角和，激发学生的学习兴趣，使课堂教学向着积极有利的方向发展.

    以多样的探究活动作为教学的

    生成点

    “三角形的内角和”教学的难点和重点是性质定理的论证过程，该过程中所渗透的方法和思路对于整个几何内容的教学有着重要的启示作用. 一般对于几何性质定理的教学采用探究式的教学方式，一般探究的过程中需要借助多样的探究活动，让学生通过体验探究的过程来完成知识生成，这也是教学的生成点.

    对于三角形的内角和的探究论证，一般采用拼图的方式，该方式的优势在于直观简洁，容易操作，因此在教学中可以设计多样的拼图活动，使学生充分参与，自我感知. 例如可以设置如下拼图活动：请大家准备一个三角形纸板，将三角形的三个内角撕下来，尝试采用拼图的方式来证明三角形的内角和等于180°. 拼图的过程学生在小学阶段已经体验过，而中学教学中需要使学生关注几个问题点：①学生拼合的方式可能略有不同，拼图的总体思路是什么？（使三个内角拼接在同一点上，形成一条直线）②拼图过程的本质是什么，主要目的是什么？（拼图过程的本质就是图形变换，主要目的就是用三个内角组成一个平角，实现未知角度的整合）

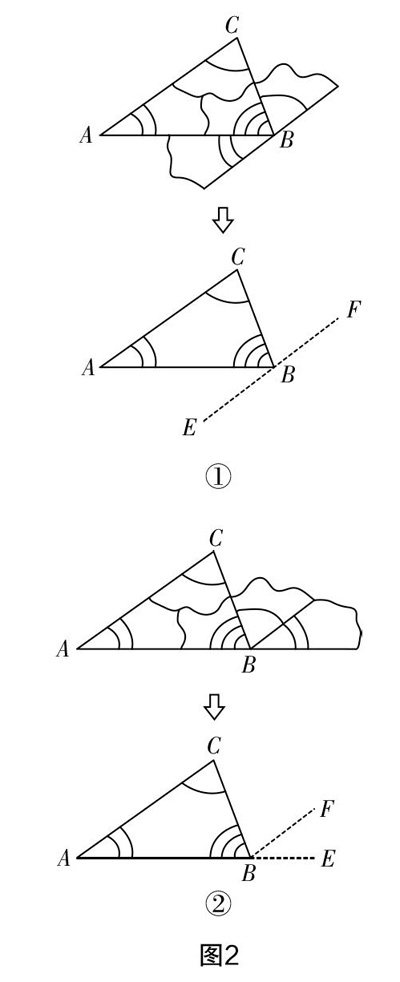
    拼图过程是相对直观的教学活动，为引导学生进一步理解，有必要结合拼图活动来理解整个过程，完成感性思维向理性思维的初步过渡，为后续的几何证明打基础. 如设置如下活动：将△ABC的三个内角撕下来后，可以采用如图2的两种方式将三角形的三个顶点拼接在同一处，请大家根据角的边线绘制虚线，并思考虚线与∠B形成的几个角分别对应原三角形中的哪个内角，进一步思考所绘制的虚线是否与原三角形的边存在平行关系.

    学生通过观察很容易发现拼图过程中角的对应关系，以及所绘制虚线BF与三角形的边AC之间是平行关系，从而深刻理解拼图的过程实际上就是等角转化的过程，即实现三个内角平移到三角形所在平面的同一顶点处，从而得到平角. 上述活动中主要涉及两大内容：一是移动拼图，二是作辅助线. 前者是后续图形变换的教学基础，后者让学生初步体验了构造辅助线的过程，体会到辅助线参与的转化策略.

    以严密的几何证明作为教学的

    发展点

    数学课堂的教学目的是培养学生的逻辑思维，让学生形成严密的数学思维，因此教学中需要设置相应的环节使学生完成感性认识到理性思考的过渡. 在知识的发展阶段需要衔接之前的拼图活动，从拼图中抽象出几何模型，通过严密的几何证明来强化学生认知，形成具有科学性的结论，这是教学的发展点.

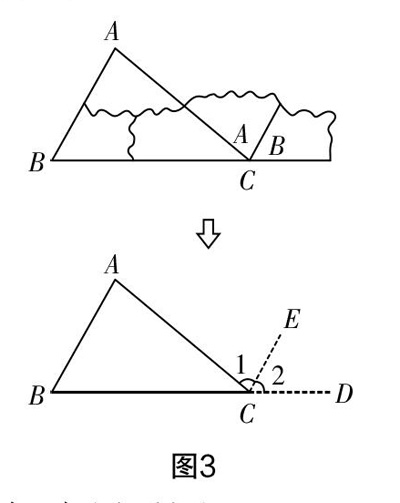
    实际教学中利用拼图模型来抽象出几何模型，让学生思考证明思路，可以设置如下活动：图3所示是某位学生将三角形三个内角拼接在一起的过程，请根据该过程的证明思路完成几何说理证明. 在实际教学中需要教师引导学生严格按照几何构造、说理的方式来进行，具体如下.

    [图3]

    已知：如图3所示，∠A、∠B、∠C是△ABC的三個内角. 求证：∠A+∠B+∠C=180°.

    证明：延长BC至点D，过△ABC的顶点C作边AB的平行线EC，因为EC∥AB，所以∠1=∠A（两直线平行，同旁内角相等），∠2=∠B（两直线平行，同位角相等）. 因为∠C+∠1+∠2=180°，所以∠A+∠B+∠C=180°，证毕.

    根据上述几何证明过程，教学引导需要分三步进行：第一步引导学生按照拼图思路绘制辅助线，即绘制与边AB相平行的直线;第二步引导学生观察分析图中的∠1和∠A，∠2和∠B分别是同旁内角和同位角中的哪种关系;第三步引导学生利用两线平行的性质定理来构建相应的等角关系，逐步完成等角代换证明.

    为培养学生思维的灵活性和多样性，在完成上述引导证明后，还可以让学生从不同的角度、不同的方位思考证明三角形的内角和为180°的方法. 如给出图4所示的拼图示意图，让学生通过自我思考，小组讨论的方式来完成图中的说理证明，教师要适时对学生的说理进行纠正，提升学生的语言表述能力.

    [图4]

    上述是从几何证明角度来完成知识发展，在该过程中完成了文字语言和几何语言之间转化，这是需要学生在初中阶段掌握的基本技能，对于学生今后的推理证明学习有着极大的帮助，因此在教学中教师需要关注学生的思维发展，有效把握学生的思维冲突来推进课堂教学.

    以开放的例题变式作为能力

    的提升点

    “三角形的内角和”的教学中主要有两大任务：一是使学生掌握相应的性质，学习证明过程，二是使学生掌握性质的应用方法. 对于后者需要以开放的例题来培养，这也是教学的能力提升点. 教学中需要适应学生的个性需要设置多变的例题，充分调动学生思维的变通性和创造性来加以解决.

    问题设置需要从两个角度进行：一是引导学生直接利用三角形的内角和性质来完成未知角的求解;二是从知识联系性出发，引导学生结合相关知识，应用性质定理分析问题. 基于上述设计原则，设计如下两道例题.

    例1如图5所示，在△ABC中，已知∠BAC=60°，∠C=45°，若AD是△ABC的角平分线，试求∠ADB的大小.

    [图5]

    例题涉及三角形的内角和性质和角平分线性质，教学时首先需要引导学生根据角平分线的性质得出∠DAC的的大小，然后引导学生利用三角形的内角和性质推理出∠ADC的大小，最后由平角的意义来获得答案. 在例题求解结束后，还可以引导学生进一步思考整个问题突破的思路，帮助学生形成新的解题策略.

    例2已知△ABC中∠A ∶ ∠B ∶ ∠C=1 ∶ 2 ∶ 3，试求∠A、∠B、∠C的大小，并判断△ABC的形状.

    对于该例题，教学中首先需要教师引导学生思考比例分配问题的求法，即通过设元的方法将三个角的大小表示出来，然后引导学生利用三角形的内角和性质构建相应的方程来求解. 該例题很好地体现了方程思想的应用，因此教学结束后可以引导学生总结方程思想解析问题的策略，即“设未知量→分析数量关系→建立方程→解方程求答案”.

    考虑到方程思想解析问题的过程较为抽象，教学时需要教师结合具体的问题，例如对于上述试题，设∠A=x，则对应的有∠B=2x，∠C=3x;分析数量关系阶段引导学生调用三角形的内角和性质，即三个内角之和为180°;建立方程阶段只需要引导学生将三个内角之间的数量关系方程化即可，即x+2x+3x=180°;最后引导学生严格按照解方程的步骤求解.

    利用开放的例题可以有效培养学生的思维能力，在例题教学时需要注重分析方法的渗透，引导学生掌握文字语言提炼、分段说理推断、逐条演绎说理的方法，逐步使学生掌握相应的解题策略，形成良好的解析思维.

    总之，“三角形的内角和”的教学需要在《数学课程标准》的基本理念指导下进行，准确把握课堂教学的起点、生成点、发展点和提升点，做好课堂教学引导，尊重学生的主体地位，使学生充分参与探究过程，使学生掌握相应知识的同时获得能力的提升.