舟山群岛某高桩码头岸坡稳定性分析
潘兴标 高华喜
摘要:本文通过采用有限元强度折减法,结合有限元分析软件,建立有限元模型,得出天然岸坡和舟山群岛某高桩码头岸坡的安全系数、塑性屈服区、位移场等,表明有限元强度折减法能够模拟出岸坡逐渐失稳的情况,桩基的存在大大加强岸坡稳定,使得岸坡潜在的滑裂面下移,在计算岸坡稳定时,要考虑桩基的抗滑作用。
关键词:高桩码头 岸坡稳定 有限元強度折减法 安全系数
中图分类号:U656 文献标识码:A
近年来,随着“海有上丝绸之路”、“江海联运”的实施和发展,我国对水路运输的要求越来越高。其中,港口是具有水陆联运设备和条件,供船舶安全进出和停泊的运输枢纽,是船舶停泊、装卸货物、上下旅客、补充给养的场所。而码头作为港口重要的一个部分,它的安全受到极大的重视。在近岸港口建设中,高桩码头[1]因其结构轻、减弱波浪效果好且适用软土地基等诸多优点成为舟山地区广泛使用的码头结构形式,而高桩码头岸坡的稳定关系到码头是否可以正常作业。
目前,对边坡稳定相关研究较多,对码头岸坡稳定研究相对较少。岸坡稳定问题直到现在一直是工程界和学术界非常关注的研究方向。自圆弧滑动法诞生以来,已经出现了许多分析土坡稳定的方法,目前根据静力平衡原理的极限平衡法,[2]由于能近似求出岸坡的安全系数而被广为采用。但是,传统的极限平衡法需要将岸坡土体假设为刚体,无法获得土体自身的应力和变形,这显然不符合实际,而且极限平衡法对存在桩基等有支护的岸坡也无法计算,极限平衡法显然不能满足岸坡稳定的计算要求。随着计算机水平的进步和有限元计算软件的发展,强度折减法由于能克服极限平衡法的缺点,被应用到有限元计算中。王元战等[3]首次用有限元强度折减法对国内某突堤码头建立有限元模型,杨熙[4]用ABAQUS有限元软件建立高桩码头桩土间相互作用的模型,证明有限元法的可行性。朱向荣[5]在研究 ABAQUS土的本构模型中探讨了MohrCoulomb模型和扩展Drucker-Prager模型的适用性,张宝华等[6]模拟天津港某岸坡模型得出岸坡失稳的判断标准。
1 有限元强度折减法
1.1有限元强度折减法的原理
1975年,Zienkiewicz等首次在有限元数值分析中提出了抗减强度折减系数的概念。抗减强度折减系数即为:外荷载保持不变,边坡坡体所发挥的最大抗减切强度与外荷载在边坡内所产生的实际剪应力之比。原理简单概括为:计算中通过不断降低边坡抗减强度参数(粘聚力、内摩擦角、折减系数),折减后的参数不断代入模型进行重复计算,直到模型达到极限破坏状态,此时的折减系数即为边坡的安全系数。用如下公式表示: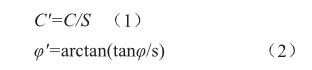
1.2有限元强度折减法的优点
与传统的极限平衡法相比,有限元强度折减法不需要事先假定滑裂面的形状和位置;可以得出岸坡的应力和位移情况;可以模拟类似桩基等支护结构与土体之间的协同作用;可以模拟出土体的塑性本构关系,且不需要假设土体为刚体。
1.3土体本构模型的选用
土体的物理力学性质非常复杂,兼具非线性、弹塑性、剪胀性各种特性且有各项异性等特点。为了更好地反映出土体在受力情况下的变形情况,国内外学者根据无数实验结果分析,得出一种土体变形特性可以用数学公式表达的模型:土体的本构模型。为了更加精确地得出岸坡土体的变形特性,选择土体本构的模型非常重要,由于理想弹塑性模型可以反映出破坏前和破坏后的土体,可以同时考虑弹性跟塑性,比较能够真实反映土体受力破坏的机理,再根据魏凯[7]的研究,本文选择弹塑性模型进行建模分析。
1.4岸坡失稳的判断依据
岸坡稳定问题作为当前岩土工程研究的三大问题之一,目前国内评价岸坡稳定的标准主要分为以下三种。
一是,通过有限元数值计算无数次的迭代,直到计算结果不收敛,计算结束,此时岸坡失稳,这是种数值计算方法,方便简单,适用于很多情况。
二是,在有限元计算中,由于受到重力作用,岸坡初始状态下土体塑性区存在于岸坡坡脚位置,随着强度参数不断折减逐渐到达坡顶,中间形成一个圆弧状的滑裂面,岸坡土体沿着此滑裂面滑动,此时岸坡失稳。
三是,最直观的岸坡失稳判断方法,在有限元计算中,通常岸坡各部分土体的位移变形是逐渐推移的,如果其中岸坡特征部位某个节点上的土体位移发生突变,那么岸坡失稳,此时的折减系数即为岸坡安全系数。
根据赵尚毅等[8]的研究,岸坡坡脚到坡顶形成的塑性贯通区为岸坡失稳的必要条件而非充分条件,结合实际条件,本文选择第一种计算结果不收敛作为评价岸坡稳定的标准。
2 工程实例分析
2.1工程简介
舟山群岛位于我国东南部,背靠经济发达的长江三角洲,是长江流域诸省的海上门户。港口具有丰富的深水岸线资源和优越的建港自然条件。舟山港作为上海国际航运中心和上海—宁波—舟山组合港的主要组成部分,港口开发是舟山未来最具潜力和竞争力的产业。
本文选取高桩码头岸坡所在岛屿位于舟山群岛东南部,与中国最大的渔港沈家门渔港相距约7.5公里。岛屿陆地整体上近似长方形,以南北走向延伸,南边陆地长为3公里,宽为1.5公里,北面陆地宽为1.2公里。此岛屿岙门较多,海岸线曲折,湾岬相间,海湾口门窄,纵深大,呈楔状,此处风浪影响较小,是良好的港口锚地。虽然原码头经过多次改造扩建,但仍不能满足本岛渔船的生产与作业需求。所以,该工程新建1座高桩码头,增加2个靠船泊位。为了作业时的人身和财产安全,本文对此新建高桩码头岸坡进行稳定性分析。
2.2模型建立
为有限元计算不那么复杂,便于数值模拟,将岸坡土体简化为单层均质弹塑性材料,服从Mohr-Coulomb[9]准则。桩基简化为线弹性材料,模型中码头岸坡设置为40m,后方桩台长13.5m,厚度0.5m,桩基全部采用50×50cm预应力混凝土方桩,其中桩长18m,其他材料参数(见表1),得出天然岸坡和高桩码头岸坡的有限元网格模型,见图1、图2。
高桩码头岸坡在建立模型时,要定义桩土接触面,[10]本文根据已有文献,选择桩底与土采用绑定(tie)约束,桩侧面与土的接触采用面对面(surface to surface)离散方法。对于桩土类问题,软件引入了“弹性滑移变形”的概念,软件会根据接触面上的单元长度确定滑移变形,计算公式采用罚(Penalty)摩擦公式,如公式所示: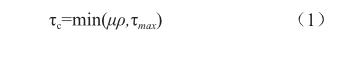
式中τc为临界剪应力,μ为滑动摩擦因数,p为法向接触压强,τmax为摩擦应力极限。
本次模型采用自由网格划分技术(Free),[11]为了使生成的单元精确地匹配种子,网格划分算法中采用进阶算法(Advancing Front)。本次模拟共分为三个分析步,第一步为软件的初始分析步,为模型添加限制两侧的水平位移和限制底部水平和竖直方向位移的约束;第二步为重力分析,为模型添加重力,方程的求解器中设为非对称分析;第三步为强度折减分析步,岸坡强度的折减将在此步完成,同样设为非对称分析。天然岸坡和高桩码头岸坡计算结果,见图3、图4。
2.3结果分析
2.3.1 天然岸坡稳定分析
由软件计算结果可知,天然岸坡随着土体强度的折减,一开始岸坡坡脚首先出现屈服,塑性区逐渐向坡顶延伸,直到折减系数达到1.47时出现(如图3)所示坡脚至坡顶的塑性贯通区。图3可以看出,滑动面大致成圆弧形状,这与传统极限平衡法分析结果一样。当折减系数超过安全系数(1.47)时,有限元软件计算不再收敛,从坡底至坡顶形成了明显的塑性贯通区,此时天然岸坡达到临界破坏状态,如再增大折减系数,岸坡土体会出现无限制的塑性流动状态,岸坡失稳。
2.3.1 高桩码头岸坡稳定分析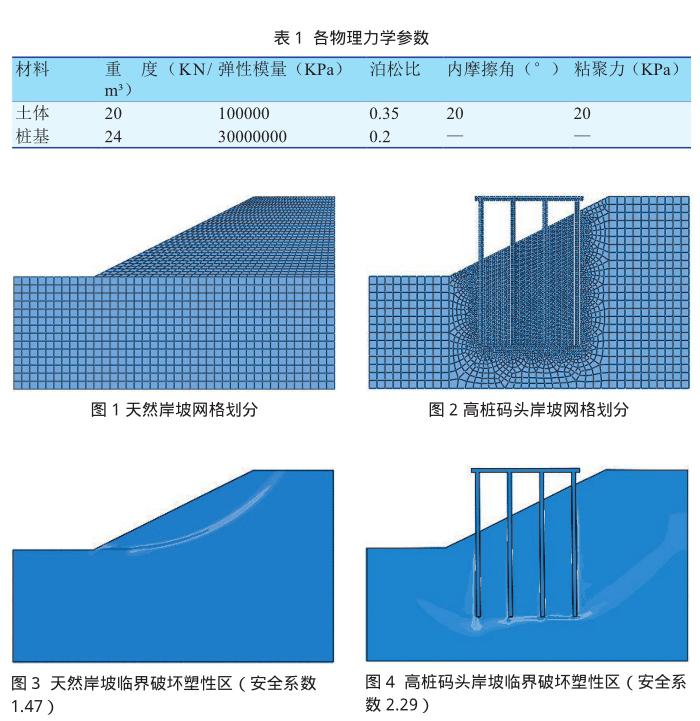
由(图4)可知,有桩基的岸坡稳定情况明显优于天然岸坡,当折减系数超过2.29时,计算才不再收敛。此时的岸坡塑性区集中在桩基底部的深层土中,桩基的存在阻碍了岸坡土体的滑动,对岸坡土体形成“遮帘作用”。进一步可以看出,此时临界状态的高桩码头岸坡并没有出现塑性贯通区,由位移矢量图可知位移最大的地方出现在桩端土层中,坡脚处土体有滑出的趋势,所以认为潜在的滑动面是由桩端土向坡顶延伸,并非圆弧滑动面,而是不规则滑动面。当折减系数继续增大时,岸坡土体才会进入无限流动状态,此时的岸坡失稳。
3 结论
通过对舟山群岛天然岸坡和某高桩码头岸坡有限元计算分析,得出以下结论:
有限元强度折减法可以较为准确地模拟出天然岸坡和有桩基岸坡逐渐失稳的状态,不需要事先假定滑裂面,不需要假设岸坡土体为刚体,并可以得出岸坡土体应力、位移、塑性区和安全系数等参数。
从塑性区的发展情况来看,塑性贯通区的形成并非岸坡失稳的充分条件,而是必要条件,有限元计算不收敛作为判断岸坡稳定标准是合理的;存在桩基的岸坡由于阻碍了土体滑动,岸坡临界破坏状态下出现的是由桩端土向坡顶延伸的不规则滑裂面,而非圆弧滑裂面。
对比天然岸坡和高桩码头岸坡破坏的临界状态,高桩码头岸坡安全系数明显得到提升,土体和桩基协同变形,桩基的存在使得岸坡潜在滑裂面下移,阻碍了土体的滑动,在以后计算岸坡稳定时,不可忽视桩基的抗滑作用。
综上所述,有限元强度折减法有着极限平衡法无法比拟的优点,但是由于有限元强度折减法的计算精度受有限元软件、网格划分方式等的影响,是否能彻底取代传统的极限平衡法还有待进一步研究。
参考文献:
[1] 韩理安.港口水工建筑物[M]. 北京:人民交通出版社, 2000.
[2] 杨明成, 郑颖人.基于极限平衡理论析局部最小安全系数法[J]. 岩土工程学报, 2002, 24(3):600- 604.
[3] 王元战, 祝振宇,张宝华,等.高桩码头岸坡稳定有限元分析[J]. 海洋工程, 2006, 24(4):27- 31.
[4] 杨熙. 基于ABAQUS软件建立高桩码头桩土相互作用有限元模型的方法[J]. 中国水运, 2012, 12(4):74- 74.
[5] 朱向荣, 王金昌. ABAQUS软件中部分土模型简介及其工程应用[J]. 岩土力学, 2004, 25(z2):144- 148.
[6] 张宝华, 黄宏宝. 强度折减有限元法分析码头岸坡稳定[J]. 水道港口,2006, 27(3):185- 187.
[7] 魏凯.武汉地铁二号线小龟山站和汉口火车站站深基坑施工仿真分析[D].华中科技大学,2007.
[8] 赵尚毅, 郑颖人, 时卫民等.用有限元强度折减法求边坡稳定安全系数[J]. 巖土工程学报,2002,24(3):343- 346.
[9] 祝振宇, 王元战, 李越松等. 高桩码头-岸坡相互作用有限元数值模拟[J]. 中国港湾建设, 2006(2):1- 4.
[10]费康, 张建伟. ABAQUS在岩土工程中的应用[M]. 北京:中国水利水电出版社, 2013.
[11]王玉镯, 傅传国. ABAQUS结构工程分析及实例详解[M]. 北京:中国建筑工业出版社, 2010.
摘要:本文通过采用有限元强度折减法,结合有限元分析软件,建立有限元模型,得出天然岸坡和舟山群岛某高桩码头岸坡的安全系数、塑性屈服区、位移场等,表明有限元强度折减法能够模拟出岸坡逐渐失稳的情况,桩基的存在大大加强岸坡稳定,使得岸坡潜在的滑裂面下移,在计算岸坡稳定时,要考虑桩基的抗滑作用。
关键词:高桩码头 岸坡稳定 有限元強度折减法 安全系数
中图分类号:U656 文献标识码:A
近年来,随着“海有上丝绸之路”、“江海联运”的实施和发展,我国对水路运输的要求越来越高。其中,港口是具有水陆联运设备和条件,供船舶安全进出和停泊的运输枢纽,是船舶停泊、装卸货物、上下旅客、补充给养的场所。而码头作为港口重要的一个部分,它的安全受到极大的重视。在近岸港口建设中,高桩码头[1]因其结构轻、减弱波浪效果好且适用软土地基等诸多优点成为舟山地区广泛使用的码头结构形式,而高桩码头岸坡的稳定关系到码头是否可以正常作业。
目前,对边坡稳定相关研究较多,对码头岸坡稳定研究相对较少。岸坡稳定问题直到现在一直是工程界和学术界非常关注的研究方向。自圆弧滑动法诞生以来,已经出现了许多分析土坡稳定的方法,目前根据静力平衡原理的极限平衡法,[2]由于能近似求出岸坡的安全系数而被广为采用。但是,传统的极限平衡法需要将岸坡土体假设为刚体,无法获得土体自身的应力和变形,这显然不符合实际,而且极限平衡法对存在桩基等有支护的岸坡也无法计算,极限平衡法显然不能满足岸坡稳定的计算要求。随着计算机水平的进步和有限元计算软件的发展,强度折减法由于能克服极限平衡法的缺点,被应用到有限元计算中。王元战等[3]首次用有限元强度折减法对国内某突堤码头建立有限元模型,杨熙[4]用ABAQUS有限元软件建立高桩码头桩土间相互作用的模型,证明有限元法的可行性。朱向荣[5]在研究 ABAQUS土的本构模型中探讨了MohrCoulomb模型和扩展Drucker-Prager模型的适用性,张宝华等[6]模拟天津港某岸坡模型得出岸坡失稳的判断标准。
1 有限元强度折减法
1.1有限元强度折减法的原理
1975年,Zienkiewicz等首次在有限元数值分析中提出了抗减强度折减系数的概念。抗减强度折减系数即为:外荷载保持不变,边坡坡体所发挥的最大抗减切强度与外荷载在边坡内所产生的实际剪应力之比。原理简单概括为:计算中通过不断降低边坡抗减强度参数(粘聚力、内摩擦角、折减系数),折减后的参数不断代入模型进行重复计算,直到模型达到极限破坏状态,此时的折减系数即为边坡的安全系数。用如下公式表示:
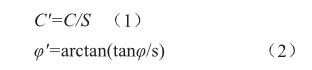
1.2有限元强度折减法的优点
与传统的极限平衡法相比,有限元强度折减法不需要事先假定滑裂面的形状和位置;可以得出岸坡的应力和位移情况;可以模拟类似桩基等支护结构与土体之间的协同作用;可以模拟出土体的塑性本构关系,且不需要假设土体为刚体。
1.3土体本构模型的选用
土体的物理力学性质非常复杂,兼具非线性、弹塑性、剪胀性各种特性且有各项异性等特点。为了更好地反映出土体在受力情况下的变形情况,国内外学者根据无数实验结果分析,得出一种土体变形特性可以用数学公式表达的模型:土体的本构模型。为了更加精确地得出岸坡土体的变形特性,选择土体本构的模型非常重要,由于理想弹塑性模型可以反映出破坏前和破坏后的土体,可以同时考虑弹性跟塑性,比较能够真实反映土体受力破坏的机理,再根据魏凯[7]的研究,本文选择弹塑性模型进行建模分析。
1.4岸坡失稳的判断依据
岸坡稳定问题作为当前岩土工程研究的三大问题之一,目前国内评价岸坡稳定的标准主要分为以下三种。
一是,通过有限元数值计算无数次的迭代,直到计算结果不收敛,计算结束,此时岸坡失稳,这是种数值计算方法,方便简单,适用于很多情况。
二是,在有限元计算中,由于受到重力作用,岸坡初始状态下土体塑性区存在于岸坡坡脚位置,随着强度参数不断折减逐渐到达坡顶,中间形成一个圆弧状的滑裂面,岸坡土体沿着此滑裂面滑动,此时岸坡失稳。
三是,最直观的岸坡失稳判断方法,在有限元计算中,通常岸坡各部分土体的位移变形是逐渐推移的,如果其中岸坡特征部位某个节点上的土体位移发生突变,那么岸坡失稳,此时的折减系数即为岸坡安全系数。
根据赵尚毅等[8]的研究,岸坡坡脚到坡顶形成的塑性贯通区为岸坡失稳的必要条件而非充分条件,结合实际条件,本文选择第一种计算结果不收敛作为评价岸坡稳定的标准。
2 工程实例分析
2.1工程简介
舟山群岛位于我国东南部,背靠经济发达的长江三角洲,是长江流域诸省的海上门户。港口具有丰富的深水岸线资源和优越的建港自然条件。舟山港作为上海国际航运中心和上海—宁波—舟山组合港的主要组成部分,港口开发是舟山未来最具潜力和竞争力的产业。
本文选取高桩码头岸坡所在岛屿位于舟山群岛东南部,与中国最大的渔港沈家门渔港相距约7.5公里。岛屿陆地整体上近似长方形,以南北走向延伸,南边陆地长为3公里,宽为1.5公里,北面陆地宽为1.2公里。此岛屿岙门较多,海岸线曲折,湾岬相间,海湾口门窄,纵深大,呈楔状,此处风浪影响较小,是良好的港口锚地。虽然原码头经过多次改造扩建,但仍不能满足本岛渔船的生产与作业需求。所以,该工程新建1座高桩码头,增加2个靠船泊位。为了作业时的人身和财产安全,本文对此新建高桩码头岸坡进行稳定性分析。
2.2模型建立
为有限元计算不那么复杂,便于数值模拟,将岸坡土体简化为单层均质弹塑性材料,服从Mohr-Coulomb[9]准则。桩基简化为线弹性材料,模型中码头岸坡设置为40m,后方桩台长13.5m,厚度0.5m,桩基全部采用50×50cm预应力混凝土方桩,其中桩长18m,其他材料参数(见表1),得出天然岸坡和高桩码头岸坡的有限元网格模型,见图1、图2。
高桩码头岸坡在建立模型时,要定义桩土接触面,[10]本文根据已有文献,选择桩底与土采用绑定(tie)约束,桩侧面与土的接触采用面对面(surface to surface)离散方法。对于桩土类问题,软件引入了“弹性滑移变形”的概念,软件会根据接触面上的单元长度确定滑移变形,计算公式采用罚(Penalty)摩擦公式,如公式所示:
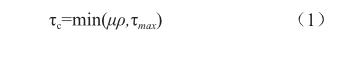
式中τc为临界剪应力,μ为滑动摩擦因数,p为法向接触压强,τmax为摩擦应力极限。
本次模型采用自由网格划分技术(Free),[11]为了使生成的单元精确地匹配种子,网格划分算法中采用进阶算法(Advancing Front)。本次模拟共分为三个分析步,第一步为软件的初始分析步,为模型添加限制两侧的水平位移和限制底部水平和竖直方向位移的约束;第二步为重力分析,为模型添加重力,方程的求解器中设为非对称分析;第三步为强度折减分析步,岸坡强度的折减将在此步完成,同样设为非对称分析。天然岸坡和高桩码头岸坡计算结果,见图3、图4。
2.3结果分析
2.3.1 天然岸坡稳定分析
由软件计算结果可知,天然岸坡随着土体强度的折减,一开始岸坡坡脚首先出现屈服,塑性区逐渐向坡顶延伸,直到折减系数达到1.47时出现(如图3)所示坡脚至坡顶的塑性贯通区。图3可以看出,滑动面大致成圆弧形状,这与传统极限平衡法分析结果一样。当折减系数超过安全系数(1.47)时,有限元软件计算不再收敛,从坡底至坡顶形成了明显的塑性贯通区,此时天然岸坡达到临界破坏状态,如再增大折减系数,岸坡土体会出现无限制的塑性流动状态,岸坡失稳。
2.3.1 高桩码头岸坡稳定分析

由(图4)可知,有桩基的岸坡稳定情况明显优于天然岸坡,当折减系数超过2.29时,计算才不再收敛。此时的岸坡塑性区集中在桩基底部的深层土中,桩基的存在阻碍了岸坡土体的滑动,对岸坡土体形成“遮帘作用”。进一步可以看出,此时临界状态的高桩码头岸坡并没有出现塑性贯通区,由位移矢量图可知位移最大的地方出现在桩端土层中,坡脚处土体有滑出的趋势,所以认为潜在的滑动面是由桩端土向坡顶延伸,并非圆弧滑动面,而是不规则滑动面。当折减系数继续增大时,岸坡土体才会进入无限流动状态,此时的岸坡失稳。
3 结论
通过对舟山群岛天然岸坡和某高桩码头岸坡有限元计算分析,得出以下结论:
有限元强度折减法可以较为准确地模拟出天然岸坡和有桩基岸坡逐渐失稳的状态,不需要事先假定滑裂面,不需要假设岸坡土体为刚体,并可以得出岸坡土体应力、位移、塑性区和安全系数等参数。
从塑性区的发展情况来看,塑性贯通区的形成并非岸坡失稳的充分条件,而是必要条件,有限元计算不收敛作为判断岸坡稳定标准是合理的;存在桩基的岸坡由于阻碍了土体滑动,岸坡临界破坏状态下出现的是由桩端土向坡顶延伸的不规则滑裂面,而非圆弧滑裂面。
对比天然岸坡和高桩码头岸坡破坏的临界状态,高桩码头岸坡安全系数明显得到提升,土体和桩基协同变形,桩基的存在使得岸坡潜在滑裂面下移,阻碍了土体的滑动,在以后计算岸坡稳定时,不可忽视桩基的抗滑作用。
综上所述,有限元强度折减法有着极限平衡法无法比拟的优点,但是由于有限元强度折减法的计算精度受有限元软件、网格划分方式等的影响,是否能彻底取代传统的极限平衡法还有待进一步研究。
参考文献:
[1] 韩理安.港口水工建筑物[M]. 北京:人民交通出版社, 2000.
[2] 杨明成, 郑颖人.基于极限平衡理论析局部最小安全系数法[J]. 岩土工程学报, 2002, 24(3):600- 604.
[3] 王元战, 祝振宇,张宝华,等.高桩码头岸坡稳定有限元分析[J]. 海洋工程, 2006, 24(4):27- 31.
[4] 杨熙. 基于ABAQUS软件建立高桩码头桩土相互作用有限元模型的方法[J]. 中国水运, 2012, 12(4):74- 74.
[5] 朱向荣, 王金昌. ABAQUS软件中部分土模型简介及其工程应用[J]. 岩土力学, 2004, 25(z2):144- 148.
[6] 张宝华, 黄宏宝. 强度折减有限元法分析码头岸坡稳定[J]. 水道港口,2006, 27(3):185- 187.
[7] 魏凯.武汉地铁二号线小龟山站和汉口火车站站深基坑施工仿真分析[D].华中科技大学,2007.
[8] 赵尚毅, 郑颖人, 时卫民等.用有限元强度折减法求边坡稳定安全系数[J]. 巖土工程学报,2002,24(3):343- 346.
[9] 祝振宇, 王元战, 李越松等. 高桩码头-岸坡相互作用有限元数值模拟[J]. 中国港湾建设, 2006(2):1- 4.
[10]费康, 张建伟. ABAQUS在岩土工程中的应用[M]. 北京:中国水利水电出版社, 2013.
[11]王玉镯, 傅传国. ABAQUS结构工程分析及实例详解[M]. 北京:中国建筑工业出版社, 2010.

