IASPEI宽频带面波震级与传统面波震级的对比
杨晶琼 杨周胜 蔡明军 许亚吉 梁勇


摘要:应用IASPEI新推荐的宽频带面波震级MS(BB)标准,选取云南数字地震台网记录到的2000~2011年云南及周边地区4.0级以上的433个地震事件为研究对象,测定其宽频带面波震级MS(BB),同时也重新测定面波震级MS,并采用线性回归和正交回归方法,对MS(BB)与MS进行对比分析研究,得到了它们之间的回归关系式。结果表明:MS比MS(BB)系统偏高,当震级较大时,二者之间差别也偏大。
关键词:宽频带面波震级MS(BB);面波震级MS;震级测定;震级转换
中图分类号:P315.6 文献标识码:A 文章编号:1000-0666(2016)02-0303-05
0 引言
震级是对地震大小的相对度量,是地震的基本参数之一,是地震预测和其它有关地震的研究中的一个重要参数。
自从Guterberg(1945)将测定近震震级ML的方法推广到远震,提出面波震级MS以来,世界各地的地震学家根据各自区域的特点相继提出了一些面波震级的计算方法。21世纪以来,全球地震台网基本实现了数字化,数字地震仪器具有频带宽、动态范围大等特点,在推动地球科学研究方面发挥了重要的作用,但其在震级测定方面还存在问题,具体表现为:近震震级、体波震级和面波震级的测定都是基于传统短周期地震仪器以及长周期地震仪器的量规函数,如果使用宽频带数字地震资料测定震级,就不能再使用传统短周期地震仪器及长周期地震仪器量规函数。数字地震仪器测定震级存在的这一问题,引起了国际地震学与地球内部物理学联合会(IASPEI)和各个国家的高度重视。为此,IASPEI于2001年在越南河内召开的大会上,成立了专门的震级工作组,开展宽频带数字地震资料震级测定的研究工作。经过几年努力,IASPEI震级工作组完成了大量的基础性研究工作,积累了大量的实际观测资料,并于2003年提出了新的震级标度和测量方法。2005年10月,在智利圣地亚哥召开的IASPEI会议上,IASPEI地震观测与资料解释委员会(CoSOI)审议通过了震级工作组提出的新的宽频带面波震级MS(BB)标准及其测量方法(IASPEI,2013)。本文将对这一标准做出说明和论述,并将其应用到云南地震台网宽频带数字记录的分析工作中,与传统面波震级MS比较,进行分析研究,以期为宽频带面波震级的广泛应用提供基础支持。
1 MS和MS(BB)震级的测定
在目前数字台网已取代模拟台网的情况下,考虑到模拟与数字记录的差异,为了统一标准,本文将全部采用数字记录资料。
笔者收集整理了云南地区数字地震台站记录到的2000~2011年云南及周边地区4.0级以上可同时测定面波震级Ms和宽频带面波震级MS(BB)的地震波形数据共433个,其中,4.0~4.9级377个,5.0~5.9级48个,6.0~6.9级7个,7.0级1个。为了能够详细研究两种震级的基本特性,本文使用同一套软件,人工测定了每个地震的两种震级测定所需要的地震波的振幅相应的周期、台站的震中距离、方位角等基础数据,然后计算两种震级值,并做相关的对比工作,拟合它们之间的关系。图1为所挑选的地震震中分布图。
1.1 面波震级MS的测定
面波震级MS是用面波测定的震级,简称“面波震级”,也就是震级国标中规定的地震震级M。它是采用中长周期地震仪SK记录的地震面波质点运动最大值(A/T)max进行测定的。
在1966年1月以后,我国开始采用郭履灿和庞明虎(1981)提出的以北京白家疃地震台为基准的面波震级公式测定面波震级,并一直使用至今。由于我国地震台网孔径的限制,在测定面波震级时都是使用震中距为130。以内的资料,计算公式为
MS=lg(A/T)max+σ(△),(1°<△<130°). (1)式中,σ(△)=1.661g(△)+3.5(1°<△<130°),A是两水平分向面波地动位移的矢量和,A=(AE2+AN2)1/2,单位μm;T是相应的周期,单位是s;σ(△)是量规函数:△是震中距离,以(°)为单位。震中距在1°<△<130°内,不同震中距选用地震面波周期值为3s
MS(BB)为宽频带面波震级,其计算方法是在垂直向速度型宽频带上直接量取面波速度的最大值,计算公式如下:
MS(BB)=lg(A/T)max+1.661g(△)+3.3,(3smax
从我国目前使用的式(1)和IASPEI新的宽频带面波震级公式(2)和(3)来看,除了测量方法差别外,从计算公式的形式看,二者数值上相差0.2。
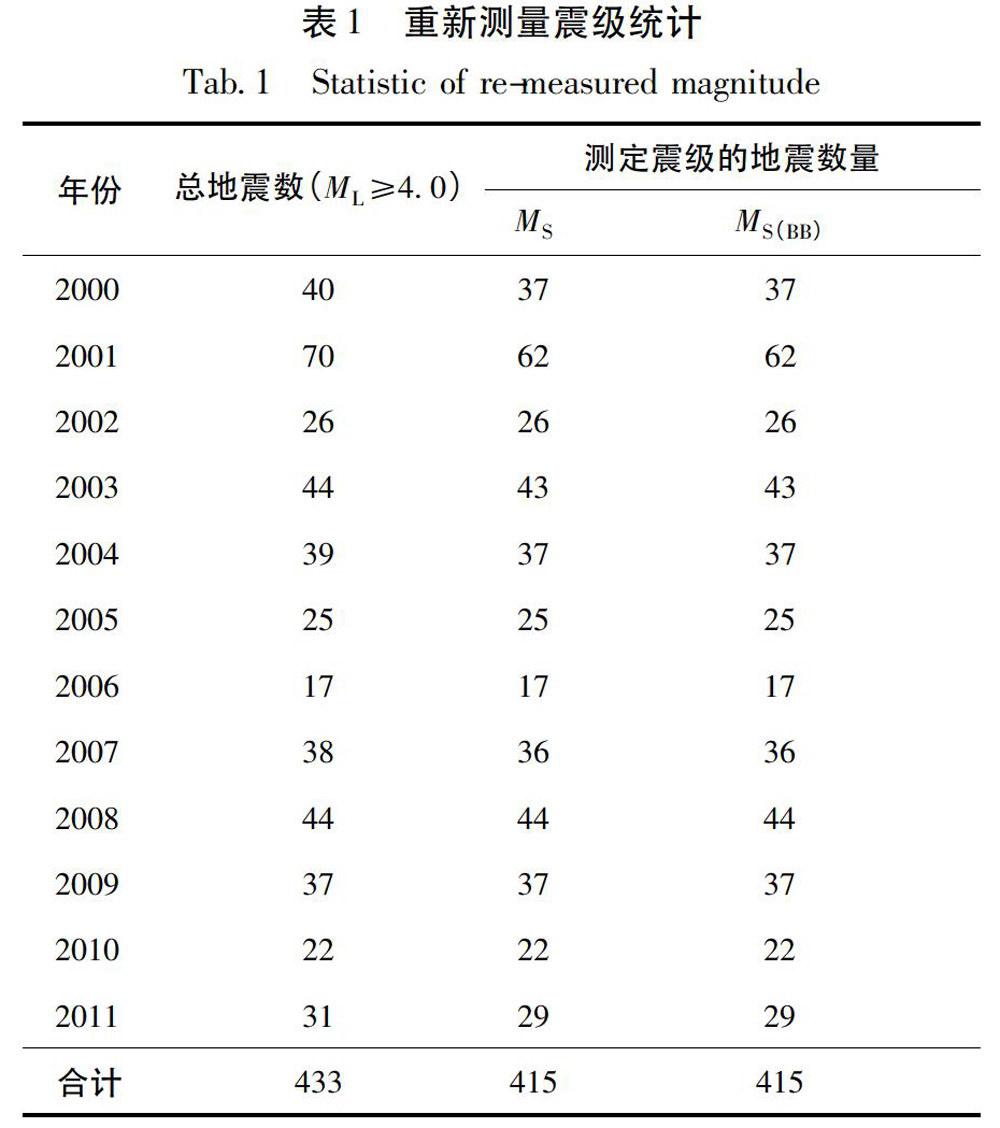
经重新测定后,获得MS和MS(BB)各415个,共830个震级。表1为重新测量震级统计。
2 回归方法
回归分析是研究事物间相关变量的数量关系的一种重要方法,本文采用线性回归和正交回归方法对云南地震台网测定得出的MS和MS(BB)值之间的关系进行全面分析。
2.1 线性回归方法
对于两个或多个存在着统计相关的随机变量,可以根据大量的观测数据来确定它们之间统计的定量关系,即推导出一定的数学公式来表达这些关系,这种公式称作回归方程。考虑将Ⅳ个数据点(xi,yi),i=1,2,3,…,N,拟合成如下直线模型的问题:
Y=AX+B. (4)
通常利用线性最小二乘回归(SR)方法就可以确定系数A和B。
SR回归方法适用于一个变量产生的偏差比另一个变量产生的偏差大的情况。确定系数A和B拟合线性公式(4)有以下两种可能(Draper,Smith,1998)。
第一种可能的情况是
SR1 Y←A1X+B1. (5)
该情况适用的条件是σ2xx→0和σ2yy>0,其中σ2xx和σ2yy分别是x和y的方差。
第二种可能的情况是
SR2 Y→A2X+B2. (6)
这种情况又称为反标准回归(carrole,Rup-pert,1996),它适用的条件是σ2xx>0和σ2yy→0。
线性回归方法只考虑一个变量产生的偏差比另一个变量产生的偏差大这种情况,因此对于线性回归关系不能使用等号,这就是在式(5)、(6)中不使用等号而使用箭头符号的原因。
2.2 正交回归方法
经典回归分析(最小二乘法)在不同领域已获得广泛应用,其应用有一重要前提,即假设自变量的值完全准确,或其观测误差与因变量的观测误差相比可忽略不计。然而本文研究的是不同测定标准下震级之间的关系,震级的测定本身存在一定误差,这导致自变量和因变量会同时存在误差,故这一重要前提往往难以实现。此时,经典的最小二乘法就难以满足数据处理的需要了,而正交回归方法则能够克服由于固定单方向最优带来的拟合稳定性差的弊端。因此,利用正交回归方法分析震级之间的关系能获得更好的结果。
采用正交回归的方法拟合式(4),以OR表示正交回归方法,则
OR Y=A3X+B3. (7)
通常采用Hesse表示方法来表示正交回归(carroll,Ruppert,1996),即把两个变量都放在等号的右边,表示右边的两个变量都在变化,即
P=nxX+nyY. (8)式中,P=B3/g,nx=-A3/g,ny=1/q,g=(1+A31/2)1/2,-nx/ny=A3。
如果把上述关系应用于震级标度Mx和My,则SR1适用于研究在Mx测量偏差较大的情况下Mx对My产生的影响,而SR2适用于研究在My测量偏差较大的情况下My对Mx产生的影响。然而,我们知道所有的震级在测量时都有可能存在一定的误差,无论是SR1还是SR2都与实际的震级测定情况有一定的差别,因此理论上用正交回归方法研究各种震级标度之间的关系应当更能接近实际的震级测定情况(Madansky,1959;Fulier,1987;刘瑞丰等,2007)。作为比较,本文分别给出了用SR1、SR2和OR方法得到的不同震级标度之间的关系式,但在对结果的分析和结论中则主要是依据OR方法来得出拟合关系式。
3 MS和MS(BB)震级的转换关系
用一般线性回归方法(SR1和SR2)和正交回归方法(OR)分别对MS和MS(BB)之间的关系进行了回归分析与对比,所得到的回归关系如表2所示。表2中RMS表示均方根,相应的回归直线如图2所示,图中直线1为SR1线性回归结果;直线2为SR2线性回归结果:直线3为OR正文回归结果;N为地震数;Rxy为正交回归的相关系数,RMSn是正交回归的均方根。
用作回归分析的资料是云南地区数字地震台站记录的2000~2011年云南及周边地区的415次地震,重新测定震级范围是3.3≤MS≤7.1。由图2可以看出,由正交回归(OR)得到的MS(BB)与MS关系直线3位于线性回归(SR1和SR2)得到的直线1和2中间。
由正交回归方法(OR)得到的结果为
MS=1.04MS(BB)-0.15. (9)
MS(BB)与MS之间有一差值,差值分布见图3。由图3看出,绝大多数地震的MS(BB)与Ms差值为-0.2~0.2,以差值为0.0的地震数量最多。
由式(9)得到的MS(BB)与Ms对照见表3。从式(9)和表3可以看出,如果以MS(BB)为基准,MS比MS(BB)系统偏高,而且当震级越大时,二者之间的差别也越大,但总体在0.2级之内。
MS平均偏高的主要原因可归结为:式(2)使用垂直向记录,而式(1)使用两个水平向记录,垂直向只包含了独立的瑞利波,而水平向却包含了叠加在一起的瑞利波和勒夫波(刘瑞丰等,2015)。除此之外,两者使用的量规函数不一样,从式(1)、(2)可以看出,两者使用的量规函数相差0.2,而这一点应该是Ms平均偏高最主要的原因。
4 讨论与结论
从理论上讲,使用垂直向测定面波震级得到的结果更稳定,因为垂直向只包含了独立的瑞利波,而水平向却包含了叠加在一起的瑞利波和勒夫波,从而导致面波震级测定结果不稳定。
传统的面波震级MS的测定,是基于一定频带宽度的模拟记录,测定它的量规函数与所使用地震仪器的频带宽度、仪器特性相关联。数字地震台网投入实际运行以后,原来的地震仪器,都已经不再使用,取而代之的是速度平坦型的宽频带数字地震仪器。因此,基于宽频带数字地震仪器的MS(BB)震级测定方法是未来发展的必然方向。
本文利用云南地区数字地震台站记录到的2000~2011年云南及周边地区4.0级以上、可同时测定宽频带面波震级MS(BB)和面波震级MS的地震波形数据,利用同一套软件,重新人工测定,并分别用线性回归(SR1和SR2)和正交回归(OR)3种方法,对MS(BB)和MS之间的关系进行回归对比分析,得到了两者之间的经验关系式,为云南地震台网开展宽频带面波震级MS(BB)的测定奠定了基础。通过对正交回归结果的分析,得到以下结论:
(1)MS(BB)与MS之间有一差值,绝大多数地震的MS(BB)与MS差值为-0.2~0.2,以差值为0.0的地震数量最多。
(2)MS(BB)与Ms之间的转换关系为:MS=1.04MS(BB)-0.15,如果以MS(BB)为基准,MS比MS(BB)系统偏高,当震级越大时,二者之间的差别也越大,但总体在0.2级之内。
衷心感谢中国地震局地球物理研究所刘瑞丰研究员对本研究给予的指导和帮助。



摘要:应用IASPEI新推荐的宽频带面波震级MS(BB)标准,选取云南数字地震台网记录到的2000~2011年云南及周边地区4.0级以上的433个地震事件为研究对象,测定其宽频带面波震级MS(BB),同时也重新测定面波震级MS,并采用线性回归和正交回归方法,对MS(BB)与MS进行对比分析研究,得到了它们之间的回归关系式。结果表明:MS比MS(BB)系统偏高,当震级较大时,二者之间差别也偏大。
关键词:宽频带面波震级MS(BB);面波震级MS;震级测定;震级转换
中图分类号:P315.6 文献标识码:A 文章编号:1000-0666(2016)02-0303-05
0 引言
震级是对地震大小的相对度量,是地震的基本参数之一,是地震预测和其它有关地震的研究中的一个重要参数。
自从Guterberg(1945)将测定近震震级ML的方法推广到远震,提出面波震级MS以来,世界各地的地震学家根据各自区域的特点相继提出了一些面波震级的计算方法。21世纪以来,全球地震台网基本实现了数字化,数字地震仪器具有频带宽、动态范围大等特点,在推动地球科学研究方面发挥了重要的作用,但其在震级测定方面还存在问题,具体表现为:近震震级、体波震级和面波震级的测定都是基于传统短周期地震仪器以及长周期地震仪器的量规函数,如果使用宽频带数字地震资料测定震级,就不能再使用传统短周期地震仪器及长周期地震仪器量规函数。数字地震仪器测定震级存在的这一问题,引起了国际地震学与地球内部物理学联合会(IASPEI)和各个国家的高度重视。为此,IASPEI于2001年在越南河内召开的大会上,成立了专门的震级工作组,开展宽频带数字地震资料震级测定的研究工作。经过几年努力,IASPEI震级工作组完成了大量的基础性研究工作,积累了大量的实际观测资料,并于2003年提出了新的震级标度和测量方法。2005年10月,在智利圣地亚哥召开的IASPEI会议上,IASPEI地震观测与资料解释委员会(CoSOI)审议通过了震级工作组提出的新的宽频带面波震级MS(BB)标准及其测量方法(IASPEI,2013)。本文将对这一标准做出说明和论述,并将其应用到云南地震台网宽频带数字记录的分析工作中,与传统面波震级MS比较,进行分析研究,以期为宽频带面波震级的广泛应用提供基础支持。
1 MS和MS(BB)震级的测定
在目前数字台网已取代模拟台网的情况下,考虑到模拟与数字记录的差异,为了统一标准,本文将全部采用数字记录资料。
笔者收集整理了云南地区数字地震台站记录到的2000~2011年云南及周边地区4.0级以上可同时测定面波震级Ms和宽频带面波震级MS(BB)的地震波形数据共433个,其中,4.0~4.9级377个,5.0~5.9级48个,6.0~6.9级7个,7.0级1个。为了能够详细研究两种震级的基本特性,本文使用同一套软件,人工测定了每个地震的两种震级测定所需要的地震波的振幅相应的周期、台站的震中距离、方位角等基础数据,然后计算两种震级值,并做相关的对比工作,拟合它们之间的关系。图1为所挑选的地震震中分布图。
1.1 面波震级MS的测定
面波震级MS是用面波测定的震级,简称“面波震级”,也就是震级国标中规定的地震震级M。它是采用中长周期地震仪SK记录的地震面波质点运动最大值(A/T)max进行测定的。
在1966年1月以后,我国开始采用郭履灿和庞明虎(1981)提出的以北京白家疃地震台为基准的面波震级公式测定面波震级,并一直使用至今。由于我国地震台网孔径的限制,在测定面波震级时都是使用震中距为130。以内的资料,计算公式为
MS=lg(A/T)max+σ(△),(1°<△<130°). (1)式中,σ(△)=1.661g(△)+3.5(1°<△<130°),A是两水平分向面波地动位移的矢量和,A=(AE2+AN2)1/2,单位μm;T是相应的周期,单位是s;σ(△)是量规函数:△是震中距离,以(°)为单位。震中距在1°<△<130°内,不同震中距选用地震面波周期值为3s
MS(BB)为宽频带面波震级,其计算方法是在垂直向速度型宽频带上直接量取面波速度的最大值,计算公式如下:
MS(BB)=lg(A/T)max+1.661g(△)+3.3,(3s
从我国目前使用的式(1)和IASPEI新的宽频带面波震级公式(2)和(3)来看,除了测量方法差别外,从计算公式的形式看,二者数值上相差0.2。
经重新测定后,获得MS和MS(BB)各415个,共830个震级。表1为重新测量震级统计。
2 回归方法
回归分析是研究事物间相关变量的数量关系的一种重要方法,本文采用线性回归和正交回归方法对云南地震台网测定得出的MS和MS(BB)值之间的关系进行全面分析。
2.1 线性回归方法
对于两个或多个存在着统计相关的随机变量,可以根据大量的观测数据来确定它们之间统计的定量关系,即推导出一定的数学公式来表达这些关系,这种公式称作回归方程。考虑将Ⅳ个数据点(xi,yi),i=1,2,3,…,N,拟合成如下直线模型的问题:
Y=AX+B. (4)
通常利用线性最小二乘回归(SR)方法就可以确定系数A和B。
SR回归方法适用于一个变量产生的偏差比另一个变量产生的偏差大的情况。确定系数A和B拟合线性公式(4)有以下两种可能(Draper,Smith,1998)。
第一种可能的情况是
SR1 Y←A1X+B1. (5)
该情况适用的条件是σ2xx→0和σ2yy>0,其中σ2xx和σ2yy分别是x和y的方差。
第二种可能的情况是
SR2 Y→A2X+B2. (6)
这种情况又称为反标准回归(carrole,Rup-pert,1996),它适用的条件是σ2xx>0和σ2yy→0。
线性回归方法只考虑一个变量产生的偏差比另一个变量产生的偏差大这种情况,因此对于线性回归关系不能使用等号,这就是在式(5)、(6)中不使用等号而使用箭头符号的原因。
2.2 正交回归方法
经典回归分析(最小二乘法)在不同领域已获得广泛应用,其应用有一重要前提,即假设自变量的值完全准确,或其观测误差与因变量的观测误差相比可忽略不计。然而本文研究的是不同测定标准下震级之间的关系,震级的测定本身存在一定误差,这导致自变量和因变量会同时存在误差,故这一重要前提往往难以实现。此时,经典的最小二乘法就难以满足数据处理的需要了,而正交回归方法则能够克服由于固定单方向最优带来的拟合稳定性差的弊端。因此,利用正交回归方法分析震级之间的关系能获得更好的结果。
采用正交回归的方法拟合式(4),以OR表示正交回归方法,则
OR Y=A3X+B3. (7)
通常采用Hesse表示方法来表示正交回归(carroll,Ruppert,1996),即把两个变量都放在等号的右边,表示右边的两个变量都在变化,即
P=nxX+nyY. (8)式中,P=B3/g,nx=-A3/g,ny=1/q,g=(1+A31/2)1/2,-nx/ny=A3。
如果把上述关系应用于震级标度Mx和My,则SR1适用于研究在Mx测量偏差较大的情况下Mx对My产生的影响,而SR2适用于研究在My测量偏差较大的情况下My对Mx产生的影响。然而,我们知道所有的震级在测量时都有可能存在一定的误差,无论是SR1还是SR2都与实际的震级测定情况有一定的差别,因此理论上用正交回归方法研究各种震级标度之间的关系应当更能接近实际的震级测定情况(Madansky,1959;Fulier,1987;刘瑞丰等,2007)。作为比较,本文分别给出了用SR1、SR2和OR方法得到的不同震级标度之间的关系式,但在对结果的分析和结论中则主要是依据OR方法来得出拟合关系式。
3 MS和MS(BB)震级的转换关系
用一般线性回归方法(SR1和SR2)和正交回归方法(OR)分别对MS和MS(BB)之间的关系进行了回归分析与对比,所得到的回归关系如表2所示。表2中RMS表示均方根,相应的回归直线如图2所示,图中直线1为SR1线性回归结果;直线2为SR2线性回归结果:直线3为OR正文回归结果;N为地震数;Rxy为正交回归的相关系数,RMSn是正交回归的均方根。
用作回归分析的资料是云南地区数字地震台站记录的2000~2011年云南及周边地区的415次地震,重新测定震级范围是3.3≤MS≤7.1。由图2可以看出,由正交回归(OR)得到的MS(BB)与MS关系直线3位于线性回归(SR1和SR2)得到的直线1和2中间。
由正交回归方法(OR)得到的结果为
MS=1.04MS(BB)-0.15. (9)
MS(BB)与MS之间有一差值,差值分布见图3。由图3看出,绝大多数地震的MS(BB)与Ms差值为-0.2~0.2,以差值为0.0的地震数量最多。
由式(9)得到的MS(BB)与Ms对照见表3。从式(9)和表3可以看出,如果以MS(BB)为基准,MS比MS(BB)系统偏高,而且当震级越大时,二者之间的差别也越大,但总体在0.2级之内。
MS平均偏高的主要原因可归结为:式(2)使用垂直向记录,而式(1)使用两个水平向记录,垂直向只包含了独立的瑞利波,而水平向却包含了叠加在一起的瑞利波和勒夫波(刘瑞丰等,2015)。除此之外,两者使用的量规函数不一样,从式(1)、(2)可以看出,两者使用的量规函数相差0.2,而这一点应该是Ms平均偏高最主要的原因。
4 讨论与结论
从理论上讲,使用垂直向测定面波震级得到的结果更稳定,因为垂直向只包含了独立的瑞利波,而水平向却包含了叠加在一起的瑞利波和勒夫波,从而导致面波震级测定结果不稳定。
传统的面波震级MS的测定,是基于一定频带宽度的模拟记录,测定它的量规函数与所使用地震仪器的频带宽度、仪器特性相关联。数字地震台网投入实际运行以后,原来的地震仪器,都已经不再使用,取而代之的是速度平坦型的宽频带数字地震仪器。因此,基于宽频带数字地震仪器的MS(BB)震级测定方法是未来发展的必然方向。
本文利用云南地区数字地震台站记录到的2000~2011年云南及周边地区4.0级以上、可同时测定宽频带面波震级MS(BB)和面波震级MS的地震波形数据,利用同一套软件,重新人工测定,并分别用线性回归(SR1和SR2)和正交回归(OR)3种方法,对MS(BB)和MS之间的关系进行回归对比分析,得到了两者之间的经验关系式,为云南地震台网开展宽频带面波震级MS(BB)的测定奠定了基础。通过对正交回归结果的分析,得到以下结论:
(1)MS(BB)与MS之间有一差值,绝大多数地震的MS(BB)与MS差值为-0.2~0.2,以差值为0.0的地震数量最多。
(2)MS(BB)与Ms之间的转换关系为:MS=1.04MS(BB)-0.15,如果以MS(BB)为基准,MS比MS(BB)系统偏高,当震级越大时,二者之间的差别也越大,但总体在0.2级之内。
衷心感谢中国地震局地球物理研究所刘瑞丰研究员对本研究给予的指导和帮助。

