一题两翼,“形”“理”兼得
陈纪韦华 陈秀娟


纵观近几何压轴题一般出现在数学试卷的最后一两题,分值大,综合性强.考查几何模块的核心知识:图形的性质与图形的变化,其结论证明或几何量计算重视考查学生的学科核心素养,具有很好的选拔性.纵观近几年各地市的几何压轴题,以发展学生的空间观念、几何直观、推理能力、运算能力为核心展开,命题趋势上大致形成两类:一是通过算证“确定性图形”,考查学生推理发现单一图形的性质;二是通过观察探究图形的“几何变换”,计算(证明)多个图形运动过程中变与不变的关系.这也与《课标》第三学段中图形与几何的内容相吻合,体现了中考命题的一致性原则.下面以2019年莆田市九年级中考质检数学卷第24题为例,探讨对几何压轴题中的“几何变换”与“解确定性图形”的思考,从战略的层面加深对试题的把握.
1 试题呈现
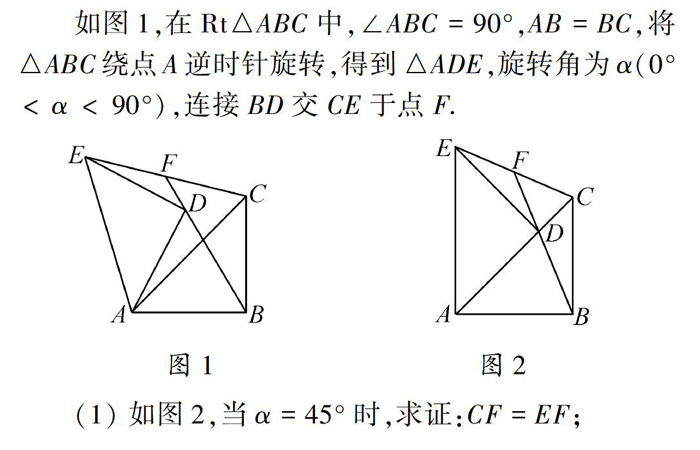
如图1,在Rt△ABC中,∠ABC=90°,AB=BC,将△ABC绕点A逆时针旋转,得到△ADE,旋转角为α(0°<α<90°),连接BD交CE于点F图1 图2
(1)如图2,当α=45°时,求证:CF=EF;
(2)在旋转过程中,
①问(1)中的结论是否仍然成立?证明你的结论;
②连接CD,当△CDF为等腰直角三角形时,求tanα2的值
本题以常见的等腰直角三角形绕点旋转为载体,第1题从一般到特殊,当旋转角为45°时,探究CF与EF的数量关系,难度小,入口宽;第2题在第1题基础上,第①题利用角与角的转化,三角形的性质等,让学生经历观察、操作、试验,探究等腰Rt△ABC在旋转过程中的不变量,动中窥静,体现了从特殊到一般,有一定的区分度;第②小题当△CDF形状确定时,通过问题设计,让学生推理计算几何量,体现了从一般回归特殊的命题设计思路,问题的解决需要学生体会“解三角形”的思想,这在某种程度上与高中的“解三角形”相衔接.三小题层层推进,题与题之间和谐共生,考查效度高.从知识维度看,考查了等腰三角形的性质和判定、直角三角形斜边中点的性质、全等三角形(相似三角形)的性质和判定,三角函数等几何核心知识;从思想方法维度看,考查了特殊与一般思想、化归与转化思想、分类与整合等;从能力维度看,分层次分水平考查了运算能力、推理能力、创新意识、空间观念等,在解答过程中注重引导学生获取信息,对图形不断提炼,重新加工,通过深入思考、分析,從而有效培养直观想象、数学抽象、数学建模、逻辑推理、数学运算等核心素养.
2 解法简析
对于第1题笔者不做分析;
(1)对于第2题第①题,研究Rt△ABC在旋转过程中的不变量,EF=CF且∠CFD=45°.有如下解法:
思路1 立足于证中点的畅想,可通过作平行构造中心对称三角形来证中点
解法1:如图3,过点E作EG∥CB交BF延长线于点G.依题∠ADB=∠ABD,故∠EDG=∠CBF,又EG∥CB,则∠G=∠CBF=∠EDG,故EG=ED,EG=BC,因此△FEG≌△FCB,得EF=CF
解法2:如图4,分别过点A,C,E,作AP⊥BF于点P,CN⊥BF于点N,EM⊥BF交BF延长线于点M.证△EMD≌△DPA,得EM=PD,证△APB≌BNC,得CN=BP,又等腰△ABD中,AP⊥BD,得PD=PB,故EM=CN,故△EMF≌△CNF,因此EF=CF图3 图4 图5
思路2 利用分割点或端点构造位似三角形证中点
解法3:如图5,过点C作CP∥DF交ED延长线于点P,EP交BC于点Q.∠EDF=∠DBC,得∠BDQ=∠DBQ,则DQ=BQ,又CP∥BD,得∠QCP=∠QBD,∠QPC=∠QDB,则∠QCP=∠QPC,可得CQ=PQ,故PD=BC=DE,因此EFCF=EDDP=1,即EF=CF
思路3:进一步分析图形旋转过程,有AEAD=ACAB=2,∠EAC=∠DAB,则△AEC∽△ADB,可得∠ACE=∠ABD,则有∠CFB=∠CAB=45°.可利用45°角构造等腰直角三角形,结合用全等三角形证线段相等来解决问题
解法4:如图6,过点D作DG⊥BF交CE于点G,连接AF.可得Rt△DFG为等腰三角形,故DF=DG,则△GED≌△FAD,可得∠AFD=∠EGD=45°,故AF⊥CE,则EF=CF图6 图7
解法5:如图7,过点B作BG⊥BF交FC延长线于点G,连接AF.可得Rt△FBG为等腰三角形,故BF=BG,故△ABF≌△CBG,可得∠AFB=∠G=45°,故AF⊥CE,则EF=CF
解法6:如图8,过点E作EG⊥CE交DF延长线于点G.可得Rt△EGF为等腰三角形,故∠G=∠CFB=45°,又DE=BC,故△GED≌FCB,可得EG=CF,又EG=EF,因此EF=CF
解法7:如图9,过点C作CG⊥CF交BF于点G.可得Rt△CFG为等腰三角形,故∠EFD=∠CGB,△EFD≌△CGB,可得EF=CG,又CG=CF,因此EF=CF图8 图9 图10
思路4 利用“三线合一”来证明EF=CF
解法8:如图10,∠BFC=∠EAD=45°,故点E,F,D,A四点共圆,则∠EFA=∠EDA=90°,又EA=AC,故EF=FC
(2)对于第2题第②题,过点A作AP⊥BD于点P.又AB=AD,故∠PAB=12∠DAB=α2,则∠CBF=α2
用“确定性三角形”的思路审视,即需要研究三角形是否确定?如何确定?三角形中的角边中哪些元素是确定的?根据这些条件如何求出来其他的元素?也即是说三角形是确定的,必是可解的,可求的.因此,依题△CDF为等腰直角三角形,故CF与DF的比值确定.又CE=2BD,CF=12CE,故CF=22BD,因此CF与BF的比值固定.即在△CFB中,∠CFB=45°,CF与BF的比值固定,因此△CFB可解,即tan∠CBF可求
第1种情况,当∠CDF=90°时,如图11,△CDF为等腰直角三角形,则CF=2DF,又CF=22BD,则DF=12BD,故CD=12BD,可得tanα2=tan∠CBD=CDBD=12;图11 图12
第2种情况,当∠FCD=90°时,如图12,△CDF为等腰直角三角形,则CF=22DF,过点C作CG⊥DF于点G.又CF=22BD,故DF=BD,CG=12DF,故CG=13BG,可得tanα2=tan∠CBG=CGBG=13综上,tanα2=12或13.
3 试题推广
(1)几何变换既是学习的对象,也是认识图形的思想与方法.几何变换是“让图形在头脑中动起来”,来认识图形变化的内在联系和本质,是培养学生看到了什么,思考到了什么,想象到了什么?通过思考想象,猜想出一些可能的结论和论证思路,这也是合情推理,也为演绎证明奠定了基础.讲清几何变换思想,能更大限度地培养学生的直观想象和逻辑推理素养.对于上述试题的第①题,探究由等腰Rt△ABC绕点A旋转中的不变量,这让笔者进一步联想到,能否对等腰Rt△ABC进一步一般化推广
思考1 将等腰Rt△ABC一般化为直角三角形时,有何结论?
如图13,在Rt△ABC中,∠ABC=90°,将△ABC绕点A逆时针旋转,得到△ADE,连接BD交CE于点F.则∠CFB=∠CAB且EF=CF图13 图14
思考2 将等腰Rt△ABC一般化为一对相似的直角三角形,有何结论?
如图14,在Rt△ABC中,∠ABC=90°,Rt△ABC∽Rt△ADE,将Rt△ADE绕点A逆时针旋转,连接BD交CE于点F.则有EFCF=tan∠ACEtan∠AEC=tan∠ABDtan∠ADB
思考3 将等腰Rt△ABC弱化为等边长的直角三角形,又有何结论?
如图15,在Rt△ABC和Rt△ADE中,∠ABC=90°,∠ADE=90°,AD=AB,将Rt△ADE绕点A逆时针旋转,连接BD交CE于点F.则有EFCF=DEBC图15 图16
思考4 将等腰Rt△ABC弱化为更一般的三角形,结论又如何?
如图16,在△ABC和△ADE中,AB=AD,DE=BC,∠EDA+∠ABC=180°,將△ADE绕点A逆时针旋转,连接BD并延长交CE于点F.则有EF=CF.图17
思考5 限制的条件越少,则研究几何的性质越本质.对于试题,可转化为核心问题“BC=DE,∠EDF=∠CBF,求证EF=CF”.这是一个典型的几何模型,可调整位置,抽象图形,如图17.因此,试题的命制技术上往往找准起点,把握特征,不断地将显性关系转化为隐性关系,构造不同载体的问题
(2)确定性思想是一种数学分析问题的方式,在解决问题时,战略上先思考问题是否“确定”,若这个问题的基本量都知道(或通过转化可得该问题的基本量),那这个问题就确定了,理论上这个问题可解,尽管可能求解时有一定的难度.后续往往不急于算解,而是在明确了做什么后,思考怎么做,做做看.例如,一个三角形的基本量确定了,该三角形的形状、大小(面积、周长、中线、高、角平分线、内切圆、外接圆等)都确定,在此基础上,解三角形——已知三角形的几个元素求其他的元素,方法为作高构造直角三角形(利用勾股定理、三角函数等),能更深刻地认识三角形的图形性质
思考6 分析后发现△CFB基本量确定,是可解的,可通过赋自变量,建立线与线,线与角之间的函数关系解三角形
如图1,若DF=mCF,BD=2CF,则BF=(2+m)CF.又cos∠CFB=CF2+BF2-BC22CF·BF,化简得BC=m2+2m+1CF.且S△CFB=12CF·BF·sin∠CFD=2(2+m)4CF2
思考7 通过条件转化,分析后发现△EFD基本量确定,也可解.因此也可求△EFD的其他元素,例如边、角、面积、周长等.
4 命题思考
试题的价值在于引导教师课堂中落实数学核心素养.一道好的试题,“形”“理”兼得,因此在解题教学中,应变试题的讲评者为试题的开发者.解题教学时先应强化通性通法的回归,例如本题先应引导学生利用几何直观从复杂的图形中分解、分析、构造基本图形,归纳出“证中点”和“解三角形”的解题模式.而后,在解题的过程中,将得到的方法、策略和思想进行内化、比较、提升.,例如可让学生思考:解题分为哪几个步骤?考查了哪些知识点及数学思想方法?还有哪些方法?最优解法是哪种?解题时“卡壳”在哪里?如何突破等,建构成自己的解题体系最后,正如数学家希尔伯特指出,“一个问题的解决意味着一系列新的问题的诞生”.解题后,教师还应当引导学生思考:一般化图形,弱化图形的形状,改变图形的位置,结论是否改变?改变、对换条件和结论,试题是否成立?变更问题的表述形式,是否可以化归?拓宽拓深试题的教学价值,实现数学核心素养的课堂落实
试题的价值还在于评价学生数学核心素养达成水平.几何压轴题对数学核心素养水平的测量,应该以核心知识(几何变换和图形性质)为基础,以数学思想方法、关键能力为引领.“一题两翼”,在几何变换中重视考查直观想象素养,“让图形动起来”,来研究推导图形间的位置数量关系,对图形的对称性等本质性质进行认识;在图形的性质中重视考查逻辑推理和数学运算素养,算证前“战略性”“确定性”地去逻辑分析问题,有条理地合情推理条件、结论间的逻辑关系,然后严密的演绎论证,准确优化的计算结果.同时,注重设问之间的综合性和层次性:分水平综合考查学生的多种核心素养.进而体现出个性差异,区分出各水平学生所达到的不同阶段性要求.

