齿轮—转子—轴承系统弯扭耦合非线性振动特性研究
陆春荣 李以农 窦作成 杨阳 杜明刚


摘要: 针对存在不对中花键联轴器齿轮-转子-轴承系统,考虑齿轮啮合力和花键联轴器啮合力的影响,建立齿輪-转子-轴承系统动力学模型,推导了弯扭耦合振动的动力学微分方程。通过进行数值仿真求解,结合随参数变化的分岔图和对应的相图及庞加莱截面图,研究了啮合频率、偏心距、花键联轴器静态不对中等参数对系统振动响应特性的影响规律,为齿轮转子耦合系统参数选择、诊断和安全运行提供了理论依据。
关键词: 非线性振动; 齿轮-转子; 弯扭耦合; 啮合频率; 花键联轴器
中图分类号: O322; TH113.1 文献标志码: A 文章编号: 1004-4523(2018)02-0238-07
DOI:10.16385/j.cnki.issn.1004-4523.2018.02.006
引 言
齿轮传动系统是一个包含齿轮副、传动轴、齿轮盘、轴承等部件的复杂结构系统,由于齿轮啮合的作用,其振动特性与简单的转子系统会有较大的区别。近年来,以Kaharaman[1]建立的单自由度齿轮系统动力学模型为基础,学者们提出了各种新的改进模型[2-3]。Lin H H[4-5]在齿轮动力学模型的基础上,采用齿轮-转子系统的扭转振动模型,对齿轮啮合力、动载系数及修缘参数进行了考察研究。Farag K Omar等[6]建立一级齿轮传动系统的9自由度模型,并且研究了传递误差等因素对系统响应的影响。欧卫林等[7]针对齿轮耦合复杂转子系统,利用轴段单元法分析了系统的弯扭耦合振动特性。窦唯等[8]针对实际高速齿轮转子系统,建立了考虑齿轮啮合及扭转作用的弯扭耦合非线性振动模型,研究了齿轮啮合刚度等参数对系统振动响应的影响规律。赵广等[9]推导了花键联轴器不对中啮合力模型,基于有限元法建立考虑啮合力作用的转子系统动力学方程,研究了不对中动态啮合力对转子系统动力学特性影响规律。大多学者对齿轮传动系统的弯扭耦合振动进行了大量的研究,但是在齿轮轴中考虑齿轮啮合力、传动轴中花键不对中啮合力等因素的少有文献提及。对于齿轮传动这样复杂的转子系统,要想正确得出系统振动特性,就得建立更贴近实际的系统动力学模型。
本文在前人所做的工作的基础上,利用集中质量法,通过对某传动装置前转向结构中齿轮转子系统考虑齿轮动态啮合力和花键轴联轴器不对中啮合力的作用和传递扭矩的弯扭耦合非线性振动特性进行仿真分析,并分析啮合频率、偏心距、静态不对中量等参数对系统动力学稳定性的影响规律。
1 齿轮-转子-轴承系统动力学模型的建立1.1 建立系统动力学模型 根据某传动装置前转向机构,并且考虑输入/输出、轴承支承等因素的影响,建立了如图1(a)所示的齿轮传动转子系统弯扭耦合非线性振动模型。从图中可以知道,该系统为一级齿轮传动减速的双平行转子系统,在考虑主/从传动齿轮以及从动齿轮传动轴较长的情况下,建立9盘质量模型,每盘的质量为mi、转动惯量为Ji以及偏心量为ei(i=1~9),盘6和盘7分别代表主/从传动齿轮所在质量盘位置,e0代表花键联轴器静态位移。图1 齿轮传动转子系统动力学模型
Fig.1 Dynamic of model of gear-rotor system
图1(b)中所示齿轮啮合模型中,在主/从动齿轮的理想中心处建立固定坐标系Ai(xi,yi)(i=6,7)假设坐标轴xi垂直于系统齿轮啮合线方向;yi平行于系统齿轮啮合线方向。主/从动齿轮旋转中心坐标系Oi(xi,yi)(i=6,7),齿轮质心坐标为Gi(xgi,ygi)(i=6,7)。主动齿轮的转角为ψ6,扭转角位移为β6;从动齿轮的转角为ψ7,扭转角位移为β7。
根据前面的定义的关系可知,主从动齿轮的转角分别为ψ6=ω1t+β6, ψ7=ω2t+β7(1)式中 t为时间。
规定在t=0时,9个质量盘的初相位都是0,且从动齿轮的转角方向为正,则齿轮质心G6,G7与旋转中心O6,O7之间的关系为xg6=x6+e6cos(- ψ6)
yg6=y6+e6sin(-ψ6)
xg7=x7+e7cosψ7
yg7=y7-e7sinψ7(2) 根据扭转振动的相对性原理和主从动齿轮啮合线方向上几何关系,可以得出啮合线上的相对位移δ= y6-y7+r6β6-r7β7+e6sinψ6-e7sinψ7-e(t),因此齿轮啮合时沿啮合线方向的动态啮合力为FG=kmf(δ)+cmf()(3)式中 km为齿轮啮合的综合啮合刚度;cm为齿轮啮合的综合啮合阻尼;r6和r7为主从齿轮的基圆半径;e(t)为齿轮啮合误差,可表示为et=ep+ersin(ωet+φe)(4)式中 ep, er为啮合误差的均值和波动幅值,取ep为0,φe为相位角,其中ωe=2πn1z1/60为齿轮副的啮合频率,n1为主动齿轮的转速,z1为主动齿轮的齿数,f(…)是非线性函数,其表达式为f(δ)=δ>bc
0,-bc≤δ≤bc
δ+bc,δ<-bc(5)式中 bc为齿侧间隙的一半。
1.2 花键联轴器啮合力模型
如图1(c)为花键联轴器受力图,联轴器传递扭矩时,会使各键产生变形,即扭转使各键产生一个啮合力,同时,两个半联轴器所在节点随系统振动又使各键产生变形,即动态位移使各键产生一个啮合力。
本文参考文献[9],假定动态位移发生在x正向,可得每个键扭转产生的啮合力为:FTi=LiKLi(6)
=T/∑zi=1LiKLiR+Li(7)式中 为各键变形产生的扭转角位移,T为扭矩,z为花键联轴器的个数,Li和KLi分别为各键等效啮合距离和刚度,R为键根圆半径。
动态位移产生的啮合力为:FDi=(e′sinφi)KLi(8)
φi=2πi-1/z(9)
e′=x+e0cosα2+y+e0sinα2(10)式中 φi为各键与x轴正向夹角,e′为联轴器动态径向位移,即两个半联轴器所在节点的相对位移,α为静态位移e0与x正向的夹角,一般情况下取α=π/2。
综上分析,得到系统花键联轴器不对中故障产生的啮合力为FLi=Li+e′sinφiKLi(11)因为每一个键的啮合力均大于零,所以FLi=Li+e′sinφiKLi,Li+e′sinφi>0
0,Li+e′sinφi≤0(12) 则联轴器不对中产生的动态啮合力分解为FX=∑zi=1Li+e′sinφiKLicosθi
FY=∑zi=1Li+e′sinφiKLisinθi(13)式中 θi为每个键作用力方向与x轴正向的夹角,其中θi=φi+π/2。
当动态位移发生在任意角度ψ时,此时,联轴器啮合力为FLx=FXcosψ-FYsinψ
FLy=FXsinψ+FYcosψ(14)1.3 建立系统动力学方程
考虑不平衡力、啮合力矩、输入输出扭矩等建立齿轮转子系统弯扭耦合动力学微分方程:
m11+k1(x1-x2)+c1(1-2)+kb1x1+
cb11=m1e1(1sinψ1+ψ21cosψ1),
m11+k1(y1-y2)+c1(1-2)+kb1y1+
cb11=m1e1(-1cosψ1+ψ21sinψ1)-m1g,
(J1+m1e21)1+kt1(β1-β2)+ct1(1-2)=
m1e1[1sinψ1-(1+g)cosψ1]-T2,
mpp+kp-1(xp-xp-1)+kp(xp-xp+1)+
cp-1(p-p-1)+cp(p-p+1)=
mpep(psinψp+ψ2pcosψp),
mpp+kp-1(yp-yp-1)+kp(yp-yp+1)+
cp-1(p-p-1)+cp(p-p+1)=
mpep(-pcosψp+ψ2psinψp)-mpg,
(Jp+mpe2p)p+kt(p-1)(βp-βp-1)+ktp(βp-βp+1)+
ct(p-1)(p-p-1)+ctp(p-p+1)=
mpep[psinψp-(p+g)cosψp],
m55+k4(x5-x4)+k5(x5-x7)+c4(5-
4)+c5(5-7)=m5e5(5sinψ5+
ψ25cosψ5)+FLx,
m55+k4(y5-y4)+k5(y5-y7)+c4(5-
4)+c5(5-7)=m5e5(-5cosψ5+
ψ25sinψ5)+FLy-m5g,
(J5+m5e25)5+kt4(β5-β4)+kt5(β5-β7)+
ct4(5-4)+ct5(5-7)=m5e5[5sinψ5-
(5+g)cosψ5],
m66+k6x6+c66+kb6x6+cb66=
m6e6(6sinψ6+ψ26cosψ6),
m66+k6y6+c66+kb6y6+cb66=
m6e6(6cosψ6-ψ26sinψ6)+FG-m6g,
(J6+m6e26)6+kt6β6+ct66=m6e6[6sinψ6+
(6+g)cosψ6]+FGr6+T1,
m77+k5(x7-x5)+k7(x7-x8)+c5(7-5)+c7(7-8)=m7e7(7sinψ7+ψ27cosψ7)-FLx,
m77+k5(y7-y5)+k7(y7-y5)+c5(7-5)+c7(7-8)=m7e7(-7cosψ7+ψ27sinψ7)-
FLy-FG-m7g,
(J7+m7e27)7+kt5(β7-β5)+kt7(β7-β8)+
ct5(7-5)+ct7(7-8)=m7e7[7sinψ7-(7+g)cosψ7]-FGr7,
m99+k8(x9-x8)+c8(9-8)+kb9x9+
cb99=m9e9(9sinψ9+ψ29cosψ9),
m99+k8(y9-y8)+c8(9-8)+kb9y9+
cb99=m9e9(-9cosψ9+ψ29sinψ9)-m9g,
(J9+m9e29)9+kt8(β9-β8)+ct8(9-8)=m9e9[9sinψ9-(9+g)cosψ9](15)
式中 p=2,3,4,8,下同。
對动力学方程进行无量纲化处理,令ω0=kav/me,kav为平均啮合刚度,me 为齿轮副等效质量,me=m6m7/(m6+m7)。令T=ω0t, ω2为从动轮角速度,无量纲化后为ω=ω2/ω0,令γ为齿轮传动比。引入特征尺寸bc,无量纲侧隙的一半D=b/bc。令X=x/bc,=dX/dT,Y=y/bc,=dY/dT,=dβ/dT,Mi=(Ji+mie2i),Kij=kj/(mibcω02),Cij=cj/(Miω0),Ktij=ktj/(Miω02),Ctij=ctj/(miω0),Kbi=kbi/(miω02),Cbi=cbi/(miω0),Ei=ei/bc,Hi=mieibc/Mi,G=g/(bcω02)。所以,得到无量纲化后动力学方程为:
1+K11(X1-X2)+C11(1-2)+Kb1X1+
Cb11=E1[1sin(ωT+θ1)+
(ω+θ1)2cos(ωT+θ1)],
1+K11(Y1-Y2)+C11(1-2)+Kb1Y1+
Cb11=E1[-1cos(ωT+θ1)+
(ω+θ1)2sin(ωT+θ1)]-G,
1+Kt11(θ1-θ2)+Ct11(1-2)=H1[1·
sin(ωT+θ1)-(1+gbc)cos(ωT+θ1)]-T2M1ω20,
p+Kp(p-1)(Xp-Xp-1)+Kpp(Xp-Xp+1)+Cp(p-1)(p-p-1)+Cpp(p-p+1)=
Ep[psin(ωT+θp)+(ω+θp)2cos(ωT+θp)],
p+Kp(p-1)(Yp-Yp-1)+Kpp(Yp-Yp+1)+Cp(p-1)(p-p-1)+Cpp(p-p+1)=
Ep[-pcos(ωT+θp)+(ω+θp)2·
sin(ωT+θp)]-G,
p+Ktp(p-1)(θp-θp-1)+Ktpp(θp-θp+1)+
Ctp(p-1)(p-p-1)+Ctpp(p-p+1)=
Hp[psin(ωT+θp)-(p+gbc)·
cos(ωT+θp)],
5+K54(X5-X4)+K55(X5-X7)+C54(5-4)+C55(5-7)=E5[5sin(ωT+θ5)+
(ω+θ5)2cos(ωT+θ5)]+FLxm5bcω20,
5+K54(Y5-Y4)+K55(Y5-Y7)+C54(5-
4)+C55(5-7)=E5[-5cos(ωT+θ5)+(ω+θ5)2sin(ωT+θ5)]+FLym5bcω20-G,
5+Kt54(θ5-θ4)+Kt55(θ5-θ7)+Ct54(5-4)+Ct55(5-7)=H5[5sin(ωT+θ5)-
(5+gbc)cos(ωT+θ5)],
6+K66X6+C666+Kb6X6+Cb66=
E6[6sin(ωγT+θ6)+(ωγ+θ6)2·
cos(ωγT+θ6)],
6+K66Y6+C666+Kb6Y6+Cb66=E6[6·
cos(ωγT+θ6)-(ωγ+θ6)2sin(ωγT+θ6)]+FGm6bcω20-G,
6+Kt66θ6+Ct666=H6[6sin(ωγT+θ6)+
(6+gbc)cos(ωγT+θ6)]+FGr6+T1M6ω20,
7+K75(X7-X5)+K77(X7-X8)+C75(7-5)+C77(7-8)=E7[7sin(ωT+θ7)+(ω+θ7)2cos(ωT+θ7)]-FLxm7bcω20,
7+K75(Y7-Y5)+K77(Y7-Y8)+C75(7-
5)+C77(7-8)=E7[-7cos(ωT+
θ7)+(ω+θ7)2sin(ωT+θ7)]-
FGm7bcω20-FLym7bcω20-G,
7+Kt75(θ7-θ5)+Kt77(θ7-θ8)+Ct75(7-5)+Ct77(7-8)=H7[7sin(ωT+θ7)-(7+gbc)cos(ωT+θ7)]-FGr7M7ω20,
9+K98(X9-X8)+C98(9-8)+Kb9X9+
Cb99=E9[9sin(ωT+θ9)+
(ω+θ9)2cos(ωT+θ9)],
9 + K98(Y9-Y8)+C98(9-8)+Kb9Y9+
Cb99=E9[-9cos(ωT+θ9)+
(ω+θ9)2sin(ωT+θ9)]-G,
9+Kt98(θ9-θ8)+Ct98(9-8)=H9[9·
sin(ωT+θ9)-(9+gbc)cos(ωT+θ9)](16)
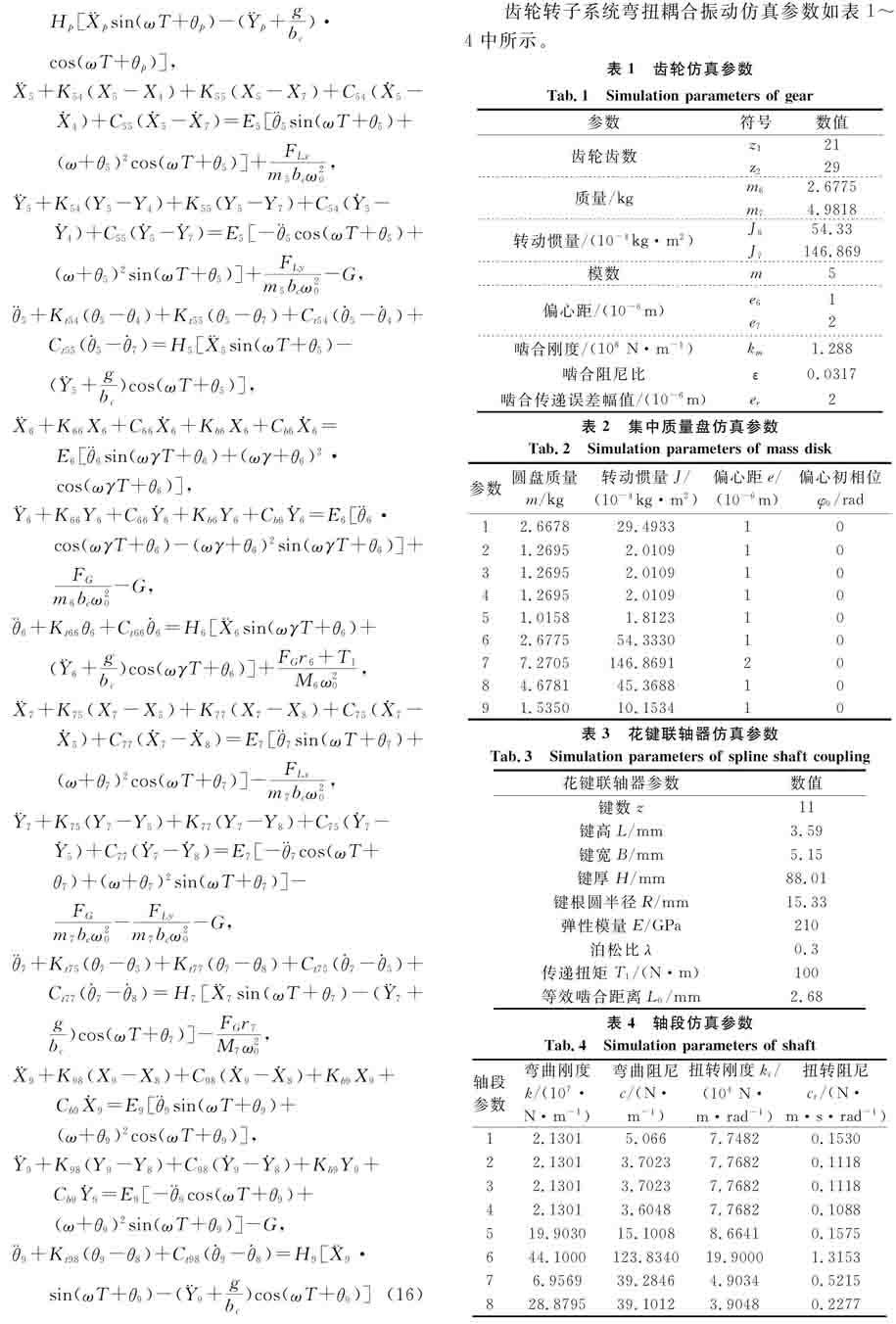
齿轮转子系统弯扭耦合振动仿真参数如表1~4中所示。
表1 齿轮仿真参数
Tab.1 Simulation parameters of gear参数符号数值齿轮齿数z1
z221
29质量/kgm6
m72.6775
4.9818转动惯量/(10-4kg·m2)J6
J754.33
146.869模数m5偏心距/(10-6m)e6
e71
2啮合刚度/(108 N·m-1)km1.288嚙合阻尼比ε0.0317啮合传递误差幅值/(10-6m)er2表2 集中质量盘仿真参数
Tab.2 Simulation parameters of mass disk参数圆盘质量
m/kg转动惯量J/
(10-4kg·m2)偏心距e/
(10-6m)〖〗偏心初相位
φ0/rad12.667829.49331021.26952.01091031.26952.01091041.26952.01091051.01581.81231062.677554.33301077.2705146.86912084.678145.36881091.535010.153410表3 花键联轴器仿真参数
Tab.3 Simulation parameters of spline shaft coupling花键联轴器参数数值键数z11键高L/mm3.59键宽B/mm5.15键厚H/mm88.01键根圆半径R/mm15.33弹性模量E/GPa210泊松比λ0.3传递扭矩T1/(N·m)100等效啮合距离L0/mm2.68表4 轴段仿真参数
Tab.4 Simulation parameters of shaft轴段
参数弯曲刚度
k/(107·
N·m-1)弯曲阻尼
c/(N·
m-1)扭转刚度kt/
(104 N·
m·rad-1)扭转阻尼
ct/(N·
m·s·rad-1)12.13015.0667.74820.153022.13013.70237.76820.111832.13013.70237.76820.111842.13013.60487.76820.1088519.903015.10088.66410.1575644.1000123.834019.90001.315376.956939.28464.90340.5215828.879539.10123.90480.2277 而对于系统支承轴承,将四处轴承均视为各向同性,不考虑交叉项。并依据《滚动轴承设计原理》,计算得到:kb1=8.1799×108 N/m,kb6=1.7465×108 N/m,kb7=8.4278×108 N/m,kb9=8.7329×108 N/m,cb1=cb6=cb7=cb9=300 N·s/m。
2 系統弯扭耦合非线性振动特性分析
系统考虑了齿轮啮合力、花键联轴器不对中啮合力等非线性因素,偏心量、转速、啮合刚度、静态不对中量等对系统动力学特性影响较大。采用变步长的4阶Runge-Kutta法求解量纲化后的动力学方程,用所求的数值解分别得到了系统在不同参数下的分岔图和庞加莱截面图,并据此为工具研究参数变化对系统振动响应的影响规律。
齿轮在6,7盘处啮合,花键不对中啮合力在5,7盘处产生,故质量盘7的振动特征最具特性,主要研究7盘的弯曲振动和扭转振动的运动分岔特性。
2.1 啮合频率的影响
取齿轮转子系统中齿轮副的半齿侧间隙值为bc=40 μm。
图2和3分别为系统随频率变化的分岔图和某些频率下的相图及庞加莱截面图。从分岔图可以看出,系统运动随啮合频率变化表现出复杂多样的分岔特性。弯曲振动和扭转振动同步运动。啮合频率较小时,运动状态较为复杂,混沌运动、单周期、多周期交替变换;啮合频率较大时,系统运动相对稳定,随着频率的增大,最终稳定在周期1运动状态。为了更好的描述系统的分岔特性,结合图3,分析相应特定频率下的相图和Poincaré图,可以得出:当ω=1.08时,相图比较混乱,且庞加莱截面图也是散乱的点,系统为混动运动;当ω=2.61时,相图为3条封闭的曲线,庞加莱聚合成3个点集,系统为周期3运动;当ω=2.86时,相图为封闭的曲线,庞加莱聚合成单个点,系统为单周期运动。图2 系统随啮合频率变化的分岔图
Fig.2 Bifurcation diagram via frequency图3 系统在不同啮合频率下的相图和庞加莱截面图
Fig.3 Phase diagram and Poincaré diagram of different frequency2.2 偏心距的影响
取啮合频率ω=2.8,其他参数保持不变,图4(a)和(b)为系统振动随偏心距变化的分岔图。从系统的分岔图中可以看出:偏心距较小时,系统表现为稳定的周期1运动;当偏心距继续增加至E=0.0012时,系统位移发生激变,而激变后又保持短暂的周期1运动,当偏心距继续增加直到E=0.0014时,系统直接由周期1运动进入混沌状态。该混沌运动状态随着偏心距E的继续增大,保持短暂的范围至E=0.0032时,系统由混沌状态再次退化为周期1运动,并且在继续增大偏心距到一定的范围,系统仍然保持着稳定的周期1运动,但是,系统的振动位移都随之明显增大。图4(c)表明:E=0.0025时,系统处于混沌运动。由此可见,在一定范围内,系统振动分岔特性随偏心距的变化相对简单,只存着周期1运动和混沌运动的转变,只是在某一范围内,发生了混沌运动。
2.3 其他系统参数的影响
齿轮是传递运动和动力的基本传动机构,建模时,考虑了齿轮输入扭矩、齿轮啮合力和花键联轴器不对中啮合力,故输入扭矩T1、齿轮啮合刚度k和花键静态不对中量E0对系统振动特性也必然会有较大影响。
图5(a)中是系统随输入扭矩T1变化时的分岔特性图。容易看出:扭矩较小时,系统运动表现为混沌运动状态;随着输入扭矩的增大,系统由混沌状态直接退化为周期1运动。但在T1=110~115 N/m小范围内,系统再次由周期1运动进入混沌运动,而继续的增大扭矩,系统稳定为周期1运动。
图5(b)中是系统随啮合刚度k变化时的分岔特性图。啮合刚度在0~0.04范围内,系统表现为混沌运动状态;刚度增大,系统稳定性增强,系统分别在k=0.05和k=0.062处发生了瞬态混沌现象,在k=0.07处出现了短暂的周期3运动,但随着刚度的继续增大,系统稳定为周期1运动。
图5(c)中是系统随啮合刚度k变化时的分岔特性图。当花键静态不对中量小于0.108时,系统在多数范围内表现为周期1运动,但周期1运动与瞬态混沌运动之间交替转变频繁,但是当E0大于0.108后,系统几乎都处在混沌运动。
可见,输入扭矩以及啮合刚度的增大,会使系统稳定性增强,而静态不对中量的增大,则会使系统运动稳定性减弱。图4 系统随偏心距变化的分岔图及对应Poincaré图
Fig.4 Bifurcation diagram via eccentric distance and Poincaré diagram图5 系统随各参数变化的分岔图
Fig.5 Bifurcation diagram via parameters3 结 论
本文数值计算得到了考虑了齿轮啮合力、花键联轴器不对中动态啮合力等因素的齿轮传动转子系统的弯、扭振动位移,借助分岔图和对应参数下的相图以及庞加莱截面图,分析了系统的动力学非线性振动特性,得到了以下结论:
(1)系统随着啮合频率的增大表现丰富的分岔特性。混沌运动、周期1运动、周期2运动等都在交错变换,高转速要比低转速稳定。
(2)偏心距对弯扭振动位移和系统的稳定性都有较大影响。偏心距增大,使得弯曲振动和扭转振动的位移都明显增大,会使得系统稳定性减弱。
(3)系统扭矩、啮合刚度等参数都会引起系统发生分岔,出现混沌运动。输入扭矩较大时,系统稳定,而较小时不稳定;啮合刚度越大,系统的稳定性越好;但静态不对中增大,系统稳定性会变差,进入混沌运动,为了保证系统的运动稳定性,必须控制齿轮转子系统中花键联轴器静态不对中的大小。
参考文献:
[1] Kahraman A, Singh R. Non-linear dynamics of a spur gear pair [J]. Journal of Sound and Vibration, 1990, 142(1): 49—75.
[2] WANG Jianhong, ZHANG Qingwei, HE Renbing. Effect of involute contact ratio on the dynamic performance of spur gear with no tooth profile modification [J]. Chinese Journal of Mechanical Engineering, 2003, 16(4): 417—421.
[3] 唐进元, 陈思雨, 钟 掘. 一种改进的齿轮非线性动力学模型[J]. 工程力学, 2008, 25(1):217—223.
TANG Jinyuan, CHEN Siyu, ZHONG Jue. A improved nonlinear model for a spur gear pair system[J]. Engineering Mechanics, 2008, 25(1): 217—223.
[4] Lin H H, Huston R L, Coy J J. On dynamic loads in parallel shaft transmissions[J]. Mechanisms Transmissions and Automation in Design, 1998, 110(2):221—229.
[5] Lin H H. Dynamic loading of spur gear with linear or parabolic tooth profile modifications[J]. Mechanism and Machine Theory, 1194, 29(8):1115—1129.
[6] Omar F K, Moustafa K A F, Emam S. Mathematical modeling of gearbox including defects with experimental verification[J]. Journal of Vibration and Control, 2011:1077546311403791.
[7] 欧卫林, 王三民, 袁 茹. 齿轮耦合复杂转子系统弯扭耦合振动分析的轴单元法[J]. 航空动力学报, 2005,20(3):434—439.
Ou Weilin,Wang Sanmin, Yuan Ru. Shaft element method for the analysis of lateral-torsional coupling vibration of a complex gear-rotor system[J]. Journal of Aerospace Power, 2005, 20(3):434—439.
[8] 窦 唯, 张 楠, 刘占生. 高速齿轮转子系统弯扭耦合振动研究[J]. 振动工程学报, 2011, 24(4):385—393.
Dou Wei, Zhang Nan, Liu Zhansheng. The coupled bending and torsional vibrations of the high-speed geared rotor-bearing system[J]. Journal of Vibration Engineering,2011, 24(4):385—393.
[9] 趙 广, 刘占山, 陈 锋,等. 花键联轴器对转子-轴承系统稳定性影响研究[J]. 振动工程学报, 2009, 22(3):280—286.
Zhao Guang, Liu Zhansheng, Chen Feng, et al. Influences of spline coupling on stability of rotor-bearing system[J]. Journal of Vibration Engineering, 2009, 22(3):280—286.
Nonlinear vibration of bending-torsion coupling
gear-rotor-bearing system
LU Chun-rong1, LI Yi-nong1, DOU Zuo-cheng1, YANG Yang2, DU Ming-gang2
(1.College of Automotive Engineering, Chongqing University, Chongqing 400030, China;
2.China North Vehicle Research Institute, Beijing 100072, China)
Abstract: The dynamic characteristics of the gear-rotor-bearing system with misalignment spline coupling are studied. Considering nonlinear mesh force of gear pairs and spline coupling, the dynamic model of the gear-rotor-bearing system is proposed and the dynamic differential equation of coupled bending and torsional nonlinear vibration is deduced. The characteristic graphs, such as the diagrams of bifurcation via parameters and the corresponding phase diagram and Poincaré diagram, are obtained through the numerical simulation. The effects of the gear mesh frequency parameter, the static displacement parameter of misalignment spline coupling etc. are studied on the system vibration response. This study can provide a theoretic reference for optimum design, fault diagnosis and safe operation of geared rotor-bear coupled system.
Key words: nonlinear vibration; gear-rotor; bending-torsion coupling; gear mesh frequency; spline coupling



摘要: 针对存在不对中花键联轴器齿轮-转子-轴承系统,考虑齿轮啮合力和花键联轴器啮合力的影响,建立齿輪-转子-轴承系统动力学模型,推导了弯扭耦合振动的动力学微分方程。通过进行数值仿真求解,结合随参数变化的分岔图和对应的相图及庞加莱截面图,研究了啮合频率、偏心距、花键联轴器静态不对中等参数对系统振动响应特性的影响规律,为齿轮转子耦合系统参数选择、诊断和安全运行提供了理论依据。
关键词: 非线性振动; 齿轮-转子; 弯扭耦合; 啮合频率; 花键联轴器
中图分类号: O322; TH113.1 文献标志码: A 文章编号: 1004-4523(2018)02-0238-07
DOI:10.16385/j.cnki.issn.1004-4523.2018.02.006
引 言
齿轮传动系统是一个包含齿轮副、传动轴、齿轮盘、轴承等部件的复杂结构系统,由于齿轮啮合的作用,其振动特性与简单的转子系统会有较大的区别。近年来,以Kaharaman[1]建立的单自由度齿轮系统动力学模型为基础,学者们提出了各种新的改进模型[2-3]。Lin H H[4-5]在齿轮动力学模型的基础上,采用齿轮-转子系统的扭转振动模型,对齿轮啮合力、动载系数及修缘参数进行了考察研究。Farag K Omar等[6]建立一级齿轮传动系统的9自由度模型,并且研究了传递误差等因素对系统响应的影响。欧卫林等[7]针对齿轮耦合复杂转子系统,利用轴段单元法分析了系统的弯扭耦合振动特性。窦唯等[8]针对实际高速齿轮转子系统,建立了考虑齿轮啮合及扭转作用的弯扭耦合非线性振动模型,研究了齿轮啮合刚度等参数对系统振动响应的影响规律。赵广等[9]推导了花键联轴器不对中啮合力模型,基于有限元法建立考虑啮合力作用的转子系统动力学方程,研究了不对中动态啮合力对转子系统动力学特性影响规律。大多学者对齿轮传动系统的弯扭耦合振动进行了大量的研究,但是在齿轮轴中考虑齿轮啮合力、传动轴中花键不对中啮合力等因素的少有文献提及。对于齿轮传动这样复杂的转子系统,要想正确得出系统振动特性,就得建立更贴近实际的系统动力学模型。
本文在前人所做的工作的基础上,利用集中质量法,通过对某传动装置前转向结构中齿轮转子系统考虑齿轮动态啮合力和花键轴联轴器不对中啮合力的作用和传递扭矩的弯扭耦合非线性振动特性进行仿真分析,并分析啮合频率、偏心距、静态不对中量等参数对系统动力学稳定性的影响规律。
1 齿轮-转子-轴承系统动力学模型的建立1.1 建立系统动力学模型 根据某传动装置前转向机构,并且考虑输入/输出、轴承支承等因素的影响,建立了如图1(a)所示的齿轮传动转子系统弯扭耦合非线性振动模型。从图中可以知道,该系统为一级齿轮传动减速的双平行转子系统,在考虑主/从传动齿轮以及从动齿轮传动轴较长的情况下,建立9盘质量模型,每盘的质量为mi、转动惯量为Ji以及偏心量为ei(i=1~9),盘6和盘7分别代表主/从传动齿轮所在质量盘位置,e0代表花键联轴器静态位移。图1 齿轮传动转子系统动力学模型
Fig.1 Dynamic of model of gear-rotor system
图1(b)中所示齿轮啮合模型中,在主/从动齿轮的理想中心处建立固定坐标系Ai(xi,yi)(i=6,7)假设坐标轴xi垂直于系统齿轮啮合线方向;yi平行于系统齿轮啮合线方向。主/从动齿轮旋转中心坐标系Oi(xi,yi)(i=6,7),齿轮质心坐标为Gi(xgi,ygi)(i=6,7)。主动齿轮的转角为ψ6,扭转角位移为β6;从动齿轮的转角为ψ7,扭转角位移为β7。
根据前面的定义的关系可知,主从动齿轮的转角分别为ψ6=ω1t+β6, ψ7=ω2t+β7(1)式中 t为时间。
规定在t=0时,9个质量盘的初相位都是0,且从动齿轮的转角方向为正,则齿轮质心G6,G7与旋转中心O6,O7之间的关系为xg6=x6+e6cos(- ψ6)
yg6=y6+e6sin(-ψ6)
xg7=x7+e7cosψ7
yg7=y7-e7sinψ7(2) 根据扭转振动的相对性原理和主从动齿轮啮合线方向上几何关系,可以得出啮合线上的相对位移δ= y6-y7+r6β6-r7β7+e6sinψ6-e7sinψ7-e(t),因此齿轮啮合时沿啮合线方向的动态啮合力为FG=kmf(δ)+cmf()(3)式中 km为齿轮啮合的综合啮合刚度;cm为齿轮啮合的综合啮合阻尼;r6和r7为主从齿轮的基圆半径;e(t)为齿轮啮合误差,可表示为et=ep+ersin(ωet+φe)(4)式中 ep, er为啮合误差的均值和波动幅值,取ep为0,φe为相位角,其中ωe=2πn1z1/60为齿轮副的啮合频率,n1为主动齿轮的转速,z1为主动齿轮的齿数,f(…)是非线性函数,其表达式为f(δ)=δ>bc
0,-bc≤δ≤bc
δ+bc,δ<-bc(5)式中 bc为齿侧间隙的一半。
1.2 花键联轴器啮合力模型
如图1(c)为花键联轴器受力图,联轴器传递扭矩时,会使各键产生变形,即扭转使各键产生一个啮合力,同时,两个半联轴器所在节点随系统振动又使各键产生变形,即动态位移使各键产生一个啮合力。
本文参考文献[9],假定动态位移发生在x正向,可得每个键扭转产生的啮合力为:FTi=LiKLi(6)
=T/∑zi=1LiKLiR+Li(7)式中 为各键变形产生的扭转角位移,T为扭矩,z为花键联轴器的个数,Li和KLi分别为各键等效啮合距离和刚度,R为键根圆半径。
动态位移产生的啮合力为:FDi=(e′sinφi)KLi(8)
φi=2πi-1/z(9)
e′=x+e0cosα2+y+e0sinα2(10)式中 φi为各键与x轴正向夹角,e′为联轴器动态径向位移,即两个半联轴器所在节点的相对位移,α为静态位移e0与x正向的夹角,一般情况下取α=π/2。
综上分析,得到系统花键联轴器不对中故障产生的啮合力为FLi=Li+e′sinφiKLi(11)因为每一个键的啮合力均大于零,所以FLi=Li+e′sinφiKLi,Li+e′sinφi>0
0,Li+e′sinφi≤0(12) 则联轴器不对中产生的动态啮合力分解为FX=∑zi=1Li+e′sinφiKLicosθi
FY=∑zi=1Li+e′sinφiKLisinθi(13)式中 θi为每个键作用力方向与x轴正向的夹角,其中θi=φi+π/2。
当动态位移发生在任意角度ψ时,此时,联轴器啮合力为FLx=FXcosψ-FYsinψ
FLy=FXsinψ+FYcosψ(14)1.3 建立系统动力学方程
考虑不平衡力、啮合力矩、输入输出扭矩等建立齿轮转子系统弯扭耦合动力学微分方程:
m11+k1(x1-x2)+c1(1-2)+kb1x1+
cb11=m1e1(1sinψ1+ψ21cosψ1),
m11+k1(y1-y2)+c1(1-2)+kb1y1+
cb11=m1e1(-1cosψ1+ψ21sinψ1)-m1g,
(J1+m1e21)1+kt1(β1-β2)+ct1(1-2)=
m1e1[1sinψ1-(1+g)cosψ1]-T2,
mpp+kp-1(xp-xp-1)+kp(xp-xp+1)+
cp-1(p-p-1)+cp(p-p+1)=
mpep(psinψp+ψ2pcosψp),
mpp+kp-1(yp-yp-1)+kp(yp-yp+1)+
cp-1(p-p-1)+cp(p-p+1)=
mpep(-pcosψp+ψ2psinψp)-mpg,
(Jp+mpe2p)p+kt(p-1)(βp-βp-1)+ktp(βp-βp+1)+
ct(p-1)(p-p-1)+ctp(p-p+1)=
mpep[psinψp-(p+g)cosψp],
m55+k4(x5-x4)+k5(x5-x7)+c4(5-
4)+c5(5-7)=m5e5(5sinψ5+
ψ25cosψ5)+FLx,
m55+k4(y5-y4)+k5(y5-y7)+c4(5-
4)+c5(5-7)=m5e5(-5cosψ5+
ψ25sinψ5)+FLy-m5g,
(J5+m5e25)5+kt4(β5-β4)+kt5(β5-β7)+
ct4(5-4)+ct5(5-7)=m5e5[5sinψ5-
(5+g)cosψ5],
m66+k6x6+c66+kb6x6+cb66=
m6e6(6sinψ6+ψ26cosψ6),
m66+k6y6+c66+kb6y6+cb66=
m6e6(6cosψ6-ψ26sinψ6)+FG-m6g,
(J6+m6e26)6+kt6β6+ct66=m6e6[6sinψ6+
(6+g)cosψ6]+FGr6+T1,
m77+k5(x7-x5)+k7(x7-x8)+c5(7-5)+c7(7-8)=m7e7(7sinψ7+ψ27cosψ7)-FLx,
m77+k5(y7-y5)+k7(y7-y5)+c5(7-5)+c7(7-8)=m7e7(-7cosψ7+ψ27sinψ7)-
FLy-FG-m7g,
(J7+m7e27)7+kt5(β7-β5)+kt7(β7-β8)+
ct5(7-5)+ct7(7-8)=m7e7[7sinψ7-(7+g)cosψ7]-FGr7,
m99+k8(x9-x8)+c8(9-8)+kb9x9+
cb99=m9e9(9sinψ9+ψ29cosψ9),
m99+k8(y9-y8)+c8(9-8)+kb9y9+
cb99=m9e9(-9cosψ9+ψ29sinψ9)-m9g,
(J9+m9e29)9+kt8(β9-β8)+ct8(9-8)=m9e9[9sinψ9-(9+g)cosψ9](15)
式中 p=2,3,4,8,下同。
對动力学方程进行无量纲化处理,令ω0=kav/me,kav为平均啮合刚度,me 为齿轮副等效质量,me=m6m7/(m6+m7)。令T=ω0t, ω2为从动轮角速度,无量纲化后为ω=ω2/ω0,令γ为齿轮传动比。引入特征尺寸bc,无量纲侧隙的一半D=b/bc。令X=x/bc,=dX/dT,Y=y/bc,=dY/dT,=dβ/dT,Mi=(Ji+mie2i),Kij=kj/(mibcω02),Cij=cj/(Miω0),Ktij=ktj/(Miω02),Ctij=ctj/(miω0),Kbi=kbi/(miω02),Cbi=cbi/(miω0),Ei=ei/bc,Hi=mieibc/Mi,G=g/(bcω02)。所以,得到无量纲化后动力学方程为:
1+K11(X1-X2)+C11(1-2)+Kb1X1+
Cb11=E1[1sin(ωT+θ1)+
(ω+θ1)2cos(ωT+θ1)],
1+K11(Y1-Y2)+C11(1-2)+Kb1Y1+
Cb11=E1[-1cos(ωT+θ1)+
(ω+θ1)2sin(ωT+θ1)]-G,
1+Kt11(θ1-θ2)+Ct11(1-2)=H1[1·
sin(ωT+θ1)-(1+gbc)cos(ωT+θ1)]-T2M1ω20,
p+Kp(p-1)(Xp-Xp-1)+Kpp(Xp-Xp+1)+Cp(p-1)(p-p-1)+Cpp(p-p+1)=
Ep[psin(ωT+θp)+(ω+θp)2cos(ωT+θp)],
p+Kp(p-1)(Yp-Yp-1)+Kpp(Yp-Yp+1)+Cp(p-1)(p-p-1)+Cpp(p-p+1)=
Ep[-pcos(ωT+θp)+(ω+θp)2·
sin(ωT+θp)]-G,
p+Ktp(p-1)(θp-θp-1)+Ktpp(θp-θp+1)+
Ctp(p-1)(p-p-1)+Ctpp(p-p+1)=
Hp[psin(ωT+θp)-(p+gbc)·
cos(ωT+θp)],
5+K54(X5-X4)+K55(X5-X7)+C54(5-4)+C55(5-7)=E5[5sin(ωT+θ5)+
(ω+θ5)2cos(ωT+θ5)]+FLxm5bcω20,
5+K54(Y5-Y4)+K55(Y5-Y7)+C54(5-
4)+C55(5-7)=E5[-5cos(ωT+θ5)+(ω+θ5)2sin(ωT+θ5)]+FLym5bcω20-G,
5+Kt54(θ5-θ4)+Kt55(θ5-θ7)+Ct54(5-4)+Ct55(5-7)=H5[5sin(ωT+θ5)-
(5+gbc)cos(ωT+θ5)],
6+K66X6+C666+Kb6X6+Cb66=
E6[6sin(ωγT+θ6)+(ωγ+θ6)2·
cos(ωγT+θ6)],
6+K66Y6+C666+Kb6Y6+Cb66=E6[6·
cos(ωγT+θ6)-(ωγ+θ6)2sin(ωγT+θ6)]+FGm6bcω20-G,
6+Kt66θ6+Ct666=H6[6sin(ωγT+θ6)+
(6+gbc)cos(ωγT+θ6)]+FGr6+T1M6ω20,
7+K75(X7-X5)+K77(X7-X8)+C75(7-5)+C77(7-8)=E7[7sin(ωT+θ7)+(ω+θ7)2cos(ωT+θ7)]-FLxm7bcω20,
7+K75(Y7-Y5)+K77(Y7-Y8)+C75(7-
5)+C77(7-8)=E7[-7cos(ωT+
θ7)+(ω+θ7)2sin(ωT+θ7)]-
FGm7bcω20-FLym7bcω20-G,
7+Kt75(θ7-θ5)+Kt77(θ7-θ8)+Ct75(7-5)+Ct77(7-8)=H7[7sin(ωT+θ7)-(7+gbc)cos(ωT+θ7)]-FGr7M7ω20,
9+K98(X9-X8)+C98(9-8)+Kb9X9+
Cb99=E9[9sin(ωT+θ9)+
(ω+θ9)2cos(ωT+θ9)],
9 + K98(Y9-Y8)+C98(9-8)+Kb9Y9+
Cb99=E9[-9cos(ωT+θ9)+
(ω+θ9)2sin(ωT+θ9)]-G,
9+Kt98(θ9-θ8)+Ct98(9-8)=H9[9·
sin(ωT+θ9)-(9+gbc)cos(ωT+θ9)](16)
齿轮转子系统弯扭耦合振动仿真参数如表1~4中所示。
表1 齿轮仿真参数
Tab.1 Simulation parameters of gear参数符号数值齿轮齿数z1
z221
29质量/kgm6
m72.6775
4.9818转动惯量/(10-4kg·m2)J6
J754.33
146.869模数m5偏心距/(10-6m)e6
e71
2啮合刚度/(108 N·m-1)km1.288嚙合阻尼比ε0.0317啮合传递误差幅值/(10-6m)er2表2 集中质量盘仿真参数
Tab.2 Simulation parameters of mass disk参数圆盘质量
m/kg转动惯量J/
(10-4kg·m2)偏心距e/
(10-6m)〖〗偏心初相位
φ0/rad12.667829.49331021.26952.01091031.26952.01091041.26952.01091051.01581.81231062.677554.33301077.2705146.86912084.678145.36881091.535010.153410表3 花键联轴器仿真参数
Tab.3 Simulation parameters of spline shaft coupling花键联轴器参数数值键数z11键高L/mm3.59键宽B/mm5.15键厚H/mm88.01键根圆半径R/mm15.33弹性模量E/GPa210泊松比λ0.3传递扭矩T1/(N·m)100等效啮合距离L0/mm2.68表4 轴段仿真参数
Tab.4 Simulation parameters of shaft轴段
参数弯曲刚度
k/(107·
N·m-1)弯曲阻尼
c/(N·
m-1)扭转刚度kt/
(104 N·
m·rad-1)扭转阻尼
ct/(N·
m·s·rad-1)12.13015.0667.74820.153022.13013.70237.76820.111832.13013.70237.76820.111842.13013.60487.76820.1088519.903015.10088.66410.1575644.1000123.834019.90001.315376.956939.28464.90340.5215828.879539.10123.90480.2277 而对于系统支承轴承,将四处轴承均视为各向同性,不考虑交叉项。并依据《滚动轴承设计原理》,计算得到:kb1=8.1799×108 N/m,kb6=1.7465×108 N/m,kb7=8.4278×108 N/m,kb9=8.7329×108 N/m,cb1=cb6=cb7=cb9=300 N·s/m。
2 系統弯扭耦合非线性振动特性分析
系统考虑了齿轮啮合力、花键联轴器不对中啮合力等非线性因素,偏心量、转速、啮合刚度、静态不对中量等对系统动力学特性影响较大。采用变步长的4阶Runge-Kutta法求解量纲化后的动力学方程,用所求的数值解分别得到了系统在不同参数下的分岔图和庞加莱截面图,并据此为工具研究参数变化对系统振动响应的影响规律。
齿轮在6,7盘处啮合,花键不对中啮合力在5,7盘处产生,故质量盘7的振动特征最具特性,主要研究7盘的弯曲振动和扭转振动的运动分岔特性。
2.1 啮合频率的影响
取齿轮转子系统中齿轮副的半齿侧间隙值为bc=40 μm。
图2和3分别为系统随频率变化的分岔图和某些频率下的相图及庞加莱截面图。从分岔图可以看出,系统运动随啮合频率变化表现出复杂多样的分岔特性。弯曲振动和扭转振动同步运动。啮合频率较小时,运动状态较为复杂,混沌运动、单周期、多周期交替变换;啮合频率较大时,系统运动相对稳定,随着频率的增大,最终稳定在周期1运动状态。为了更好的描述系统的分岔特性,结合图3,分析相应特定频率下的相图和Poincaré图,可以得出:当ω=1.08时,相图比较混乱,且庞加莱截面图也是散乱的点,系统为混动运动;当ω=2.61时,相图为3条封闭的曲线,庞加莱聚合成3个点集,系统为周期3运动;当ω=2.86时,相图为封闭的曲线,庞加莱聚合成单个点,系统为单周期运动。图2 系统随啮合频率变化的分岔图
Fig.2 Bifurcation diagram via frequency图3 系统在不同啮合频率下的相图和庞加莱截面图
Fig.3 Phase diagram and Poincaré diagram of different frequency2.2 偏心距的影响
取啮合频率ω=2.8,其他参数保持不变,图4(a)和(b)为系统振动随偏心距变化的分岔图。从系统的分岔图中可以看出:偏心距较小时,系统表现为稳定的周期1运动;当偏心距继续增加至E=0.0012时,系统位移发生激变,而激变后又保持短暂的周期1运动,当偏心距继续增加直到E=0.0014时,系统直接由周期1运动进入混沌状态。该混沌运动状态随着偏心距E的继续增大,保持短暂的范围至E=0.0032时,系统由混沌状态再次退化为周期1运动,并且在继续增大偏心距到一定的范围,系统仍然保持着稳定的周期1运动,但是,系统的振动位移都随之明显增大。图4(c)表明:E=0.0025时,系统处于混沌运动。由此可见,在一定范围内,系统振动分岔特性随偏心距的变化相对简单,只存着周期1运动和混沌运动的转变,只是在某一范围内,发生了混沌运动。
2.3 其他系统参数的影响
齿轮是传递运动和动力的基本传动机构,建模时,考虑了齿轮输入扭矩、齿轮啮合力和花键联轴器不对中啮合力,故输入扭矩T1、齿轮啮合刚度k和花键静态不对中量E0对系统振动特性也必然会有较大影响。
图5(a)中是系统随输入扭矩T1变化时的分岔特性图。容易看出:扭矩较小时,系统运动表现为混沌运动状态;随着输入扭矩的增大,系统由混沌状态直接退化为周期1运动。但在T1=110~115 N/m小范围内,系统再次由周期1运动进入混沌运动,而继续的增大扭矩,系统稳定为周期1运动。
图5(b)中是系统随啮合刚度k变化时的分岔特性图。啮合刚度在0~0.04范围内,系统表现为混沌运动状态;刚度增大,系统稳定性增强,系统分别在k=0.05和k=0.062处发生了瞬态混沌现象,在k=0.07处出现了短暂的周期3运动,但随着刚度的继续增大,系统稳定为周期1运动。
图5(c)中是系统随啮合刚度k变化时的分岔特性图。当花键静态不对中量小于0.108时,系统在多数范围内表现为周期1运动,但周期1运动与瞬态混沌运动之间交替转变频繁,但是当E0大于0.108后,系统几乎都处在混沌运动。
可见,输入扭矩以及啮合刚度的增大,会使系统稳定性增强,而静态不对中量的增大,则会使系统运动稳定性减弱。图4 系统随偏心距变化的分岔图及对应Poincaré图
Fig.4 Bifurcation diagram via eccentric distance and Poincaré diagram图5 系统随各参数变化的分岔图
Fig.5 Bifurcation diagram via parameters3 结 论
本文数值计算得到了考虑了齿轮啮合力、花键联轴器不对中动态啮合力等因素的齿轮传动转子系统的弯、扭振动位移,借助分岔图和对应参数下的相图以及庞加莱截面图,分析了系统的动力学非线性振动特性,得到了以下结论:
(1)系统随着啮合频率的增大表现丰富的分岔特性。混沌运动、周期1运动、周期2运动等都在交错变换,高转速要比低转速稳定。
(2)偏心距对弯扭振动位移和系统的稳定性都有较大影响。偏心距增大,使得弯曲振动和扭转振动的位移都明显增大,会使得系统稳定性减弱。
(3)系统扭矩、啮合刚度等参数都会引起系统发生分岔,出现混沌运动。输入扭矩较大时,系统稳定,而较小时不稳定;啮合刚度越大,系统的稳定性越好;但静态不对中增大,系统稳定性会变差,进入混沌运动,为了保证系统的运动稳定性,必须控制齿轮转子系统中花键联轴器静态不对中的大小。
参考文献:
[1] Kahraman A, Singh R. Non-linear dynamics of a spur gear pair [J]. Journal of Sound and Vibration, 1990, 142(1): 49—75.
[2] WANG Jianhong, ZHANG Qingwei, HE Renbing. Effect of involute contact ratio on the dynamic performance of spur gear with no tooth profile modification [J]. Chinese Journal of Mechanical Engineering, 2003, 16(4): 417—421.
[3] 唐进元, 陈思雨, 钟 掘. 一种改进的齿轮非线性动力学模型[J]. 工程力学, 2008, 25(1):217—223.
TANG Jinyuan, CHEN Siyu, ZHONG Jue. A improved nonlinear model for a spur gear pair system[J]. Engineering Mechanics, 2008, 25(1): 217—223.
[4] Lin H H, Huston R L, Coy J J. On dynamic loads in parallel shaft transmissions[J]. Mechanisms Transmissions and Automation in Design, 1998, 110(2):221—229.
[5] Lin H H. Dynamic loading of spur gear with linear or parabolic tooth profile modifications[J]. Mechanism and Machine Theory, 1194, 29(8):1115—1129.
[6] Omar F K, Moustafa K A F, Emam S. Mathematical modeling of gearbox including defects with experimental verification[J]. Journal of Vibration and Control, 2011:1077546311403791.
[7] 欧卫林, 王三民, 袁 茹. 齿轮耦合复杂转子系统弯扭耦合振动分析的轴单元法[J]. 航空动力学报, 2005,20(3):434—439.
Ou Weilin,Wang Sanmin, Yuan Ru. Shaft element method for the analysis of lateral-torsional coupling vibration of a complex gear-rotor system[J]. Journal of Aerospace Power, 2005, 20(3):434—439.
[8] 窦 唯, 张 楠, 刘占生. 高速齿轮转子系统弯扭耦合振动研究[J]. 振动工程学报, 2011, 24(4):385—393.
Dou Wei, Zhang Nan, Liu Zhansheng. The coupled bending and torsional vibrations of the high-speed geared rotor-bearing system[J]. Journal of Vibration Engineering,2011, 24(4):385—393.
[9] 趙 广, 刘占山, 陈 锋,等. 花键联轴器对转子-轴承系统稳定性影响研究[J]. 振动工程学报, 2009, 22(3):280—286.
Zhao Guang, Liu Zhansheng, Chen Feng, et al. Influences of spline coupling on stability of rotor-bearing system[J]. Journal of Vibration Engineering, 2009, 22(3):280—286.
Nonlinear vibration of bending-torsion coupling
gear-rotor-bearing system
LU Chun-rong1, LI Yi-nong1, DOU Zuo-cheng1, YANG Yang2, DU Ming-gang2
(1.College of Automotive Engineering, Chongqing University, Chongqing 400030, China;
2.China North Vehicle Research Institute, Beijing 100072, China)
Abstract: The dynamic characteristics of the gear-rotor-bearing system with misalignment spline coupling are studied. Considering nonlinear mesh force of gear pairs and spline coupling, the dynamic model of the gear-rotor-bearing system is proposed and the dynamic differential equation of coupled bending and torsional nonlinear vibration is deduced. The characteristic graphs, such as the diagrams of bifurcation via parameters and the corresponding phase diagram and Poincaré diagram, are obtained through the numerical simulation. The effects of the gear mesh frequency parameter, the static displacement parameter of misalignment spline coupling etc. are studied on the system vibration response. This study can provide a theoretic reference for optimum design, fault diagnosis and safe operation of geared rotor-bear coupled system.
Key words: nonlinear vibration; gear-rotor; bending-torsion coupling; gear mesh frequency; spline coupling

