《基于前景价值最大化的PPP项目政企匹配决策研究》-管理学论文，会计论文-论文范文参考-科学狗论文网

标题

基于前景价值最大化的PPP项目政企匹配决策研究

范文

段世霞孙瑞

【摘要】为有效配置社会资本，增强政府公共产品和服务供给能力，PPP模式近年来在基础设施和公共服务领域得到广泛应用，而如何选择PPP项目合作伙伴实现最优政企匹配是PPP项目成功的关键。从政企匹配角度入手，结合PPP项目政企双方主体地位，构建基于前景价值最大化的匹配决策模型。区别于经济人假设下效用最大化决策原则，该模型考虑了双方心理感知对决策行为的影响，并以双方心理期望为各自决策参照点计算感知收益和前景价值，构建益损矩阵和前景矩阵，从而形成含有双方前景价值最大化的匹配模型，并在此过程中引入三参数区间灰数对决策指标属性加以界定。研究结果表明，政企双方心理期望对匹配结果有着重要影响，而以参照依赖为核心思想的前景理论更适于分析PPP项目政企匹配决策行为，指导政企双方做出决策，实现最优政企匹配。

【关键词】 PPP项目; 政企匹配; 前景理论; 参照点

【中图分类号】 F284 ?【文献标识码】 A ?【文章编号】 1004-5937（2020）16-0082-07

一、引言

PPP（Public-Private Partnership）模式是政府为增强公共产品和服务供给能力、提高供给效率，通过特许经营、购买服务、股权合作等与社会资本建立的一种融资方式，并由此与社会资本形成“利益共享、风险分担”的合作伙伴关系。PPP进入我国以来，其在不断修正中发展前进，从最初的探索阶段（1984—1993年）、小范围试点阶段（1994—2002年）、逐步推广阶段（2003—2008年），到调整反复阶段（2009—2012年）、大力推广阶段（2013—2016年）直至目前的规范发展阶段（2017年以来），PPP模式在中国的发展呈螺旋式上升趋势。PPP模式的推广与应用也极大地激发了社会资本活力，有效缓解了财政压力。据财政部PPP中心公布，截至2018年12月末，PPP项目管理库累计8 556个项目，总投资额12.90万亿元。2019年3月11日，财政部发布《关于推进政府和社会资本合作规范发展的实施意见》（财金〔2019〕10号），为PPP的健康发展提供了坚实保障。然而，PPP项目由于融资结构复杂、风险高、投资回收期长等特点，项目不能成功落地的情况仍时有发生。2019年7月22日，财政部办公厅印发了关于征求《政府会计准则第10号——政府和社会资本合作安排》及应用指南意见的函（财办会〔2019〕22号）。目前虽有各项政策的引导与加持，部分社会资本企业仍对PPP项目的合作积极性不高，政府选择合作伙伴时也是尤为谨慎。为此，针对PPP项目合作伙伴选择问题进行深入研究，对助力PPP行稳致远具有正向推动作用。

二、文献综述

目前国内学者对PPP的研究主要以风险分担、收益分配为焦点，涉及PPP项目特许运营期、关键成功因素、控制权配置、补偿机制等方面，从多视角提供了对PPP内涵本质的理解与思考。随着PPP项目实践的不断深入，PPP研究的关注焦点也逐步从一系列具体研究收敛于围绕PPP项目如何形成稳定合作关系的研究，而选择良好的合作伙伴是“婚姻”稳定的关键。韩立红等[1]运用多层次灰色关联分析法对影响社会资本选择的因素进行分析。费小燕[2]基于模糊综合评价法对跨境电商PPP项目的社会资本选择进行指标体系的构建。宋波等[3]基于多目标群决策算法设计了PPP项目公私合作伙伴的选择方案。任志涛等[4]对“两标并一标”背景下PPP+EPC项目社会资本的适格性进行研究。石世英等[5]立足伙伴关系思维，引入注意力和预期感知扩展计划行为理论，构建PPP项目伙伴关系维系行为意愿的研究框架。以上研究成果主要聚焦于从单一角度对社会资本选择提供建议，而良好合作伙伴关系的形成是双向选择的结果。从政企匹配角度入手研究合作伙伴选择是形成稳定合作关系促进PPP项目有序发展的关键切入点。目前仅有丰景春等[6]运用灰靶决策理论构建了政企匹配决策模型以及任志涛等[7]以满意度最大化为目标建立了针对不同类型评价信息的模糊多目标优化决策模型。政府和企业在进行PPP项目匹配决策时并非独立于社会环境中，做出匹配行为的同时受到不同层次因素的影响，表现出行为决策的“有限理性”或“非理性”。为此，在PPP项目政企匹配问题中考虑政府和企业决策时的“有限理性”行为，对形成稳定有效的合作伙伴关系促进PPP模式的良性发展具有重要意义，而有关研究忽略了这一点。

在行为人遵循有限理性的假说下，如何将行为人的心理因素考虑在决策中进而得到合理科学的决策结果，前景理论的提出填补了这一空白。前景理论是Kahneman et al.[8]基于一系列现代心理学理论研究而提出的创新性研究成果，研究了行为人在不确定情况下决策时，由于受到认识机制的局限而导致不理性行为的发生。该理论源于行为经济学，其提出后在股票、证券等投资组合研究中应用较为成熟，近年来，越来越多的学者将其应用于多属性风险型决策中。

左文明等[9]基于前景理論构建了网络消费者多属性行为决策模型。王娟等[10]针对属性权重未知，属性值为三角犹豫模糊元的多属性决策问题，提出了一种基于前景理论和模糊结构元的决策分析方法。而在PPP领域中，鲜有学者将前景理论与PPP的各项研究结合，PPP项目复杂的现实状况和决策者的有限理性行为亟须吸收合理的理论思想以便更好地指导实践。因此，本文运用前景理论为构建PPP项目政企匹配模型提供理论支撑，在匹配决策中充分考虑政企双方的心理感知，为做出科学合理的决策提供参考。

三、政企匹配问题描述

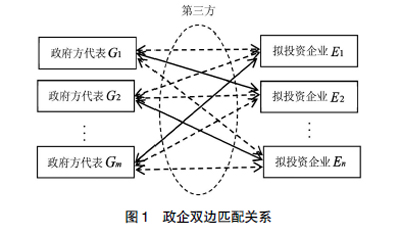
在PPP项目合作伙伴选择过程中，参与主体为政府部门、拟投资企业、第三方（招投标代理机构）。政府部门以PPP模式发起的项目迫切需要社会资本的注入，与此同时众多企业也拥有了机会进入公共服务领域。而在此过程中，合作伙伴关系的建立是一个双边匹配的问题，政府部门对有意愿合作的企业进行优化选择，以达到项目的顺利实施与运营从而实现社会受益，企业对政府授权的项目的各个方面进行选择与考量，以实现投资回报的稳定性和企业信誉的提升。第三方在匹配过程中为最大限度规避负面行为的发生发挥着桥梁作用。

在明确政企双方的匹配关系前，首先对主体进行具体描述：以政府授权的项目代表视为政府方代表，设G={G1，G2，…，Gi，…，Gm}为政府方代表集合，其中Gi表示第i个政府方代表，i=1，2，…，m，m≥2;E={E1，E2，…，Ei，…，En}为拟投资企业集合，其中Ej表示第j个拟投资企业，j=1，2，…，n;n≥2，匹配关系如图1所示。

为做出合作关系更为稳定的匹配决策，合作关系稳定是基于双方满意度和匹配度而言，双方满意度越高，匹配度越高，合作关系也就更稳定。政府方代表在寻找合作企业时往往会考虑企业的资质、项目业绩、资金状况、企业信誉等;拟投资企业也会对投资环境、政策导向、项目投资回收期、政府担保水平等进行考量。可以得出，政企匹配问题是一个基于双向选择的多属性决策问题。

设X=[X1，X2，…，Xk，…，Xe]为政府方代表Gi对拟投资企业Ej属性的满意度评价集合，Xk为拟投资企业的第k个属性，k={1，2，…，e}，且X1，X2，…，Xk，…，Xe具有獨立可加性。

U={u1，u2，…，uk，…，ue}为政府方代表Gi对拟投资企业Ej进行满意度评价的各个属性权重，同时满足ue≥0， uk=1。

P=[pki]m×e为政府方代表Gi对拟投资企业Ej关于属性集合X的期望水平矩阵，p ?为政府方代表Gi对拟投资企业Ej的第k个属性的期望值。

Q=[q ?]n×e为第三方机构对拟投资企业Ej关于属性集合X的实际评价矩阵，q ?为第三方机构对拟投资企业Ej针对属性Xk实际评价的属性值。

同理，进行拟投资企业对政府方代表的匹配描述：记Y=[Y1，Y2，…，Yl，…，Yf]为拟投资企业Ej对政府方代表Gi的满意度评价的属性集合，Yl为第l个属性，l={1，2，3，…，f}，Y1，Y2，…，Yl，…，Yf具有独立可加性。

=（ 1， 2，…， l，…， f）为拟投资企业Ej对政府方代表Gi进行满意度评价的各个属性权重，且ul≥0， ?l=1。

=[ ? ]m×f为拟投资企业Ej对政府方代表Gi关于属性集合Y的期望水平矩阵， ? 为拟投资企业Ej对政府方代表Gi关于第l个属性的期望值。

=[ ? ]m×f为第三方机构对政府方代表Gi关于属性集合Y的实际评价矩阵， ? 为第三方机构对政府方代表Gi针对属性Yl实际评价的属性值。

四、模型构建与求解

PPP项目特征复杂，涉及多方利益，政府方代表和拟投资企业在做出匹配决策时易受到心理因素和认知偏差的影响。若采用传统的基于期望效用的研究方法，忽视掉政企双方的主体性，则难以做出令双方满意度高的匹配结果。政府在选取拟投资企业作为合作伙伴时呈现有限理性，做出最终决策的同时不仅有客观理性的判断更有心理感知的影响。同理，企业在选取经政府授权的项目时同样易受到心理因素的影响。前景理论指出，决策是一个动态的过程，行为人在关注最终收益的同时更加注重根据参照点获得的感知收益，即存在参照依赖，而参照点为决策行为人的心理参考点。前景理论利用价值函数v（x）取代了效用函数，价值函数是反映行为人当期状态相对于参照点的收益与损失，体现的是财富的相对水平而非传统意义上财富的绝对值。

Kahneman et al.[11]的前景理论价值函数v（x）为：

v（x）=（x-x0）α ? ?x-x0≥0-λ（x0-x）β ? ? x-x0<0 ? （1）

其中，x0为参照点，x-x0≥0为感知收益，x-x0<0为感知损失，行为人注重的是相对于参照点（x0）的偏离程度，λ表示行为人对损失的厌恶程度，α表示行为人对于收益的敏感度，β表示行为人对于损失的敏感度。在面对等量的收益和损失时，行为人对损失的心理感知更为敏感，导致价值函数以参照点为分界线在图像中呈S型，参考点之上即收益区域呈现凸状，参考点之下即损失区域呈现凹形，且在损失区域的图形比收益区域更为陡峭。由此，更贴切地描述出有限理性人的决策行为。

基于前景理论构建匹配模型，其中参照点的选取是第一步，参照点的确立需真实反映行为人的心理感知和行为偏好，对模型是否真实适用于实践具有重要的影响。而政府方代表和拟投资企业的心理期望较真实地反映主体的心理感受，本文拟将政企双方主体给出的期望水平分别作为各自的参照点，即p ?为政府方代表（Gi）对拟投资企业（Ej）的第k个属性的参照点， ? 为拟投资企业（Ej）对政府方代表（Gi）第l个属性的参照点。

由于双方对期望水平的描述以及第三方对政企双方属性的评价很难用数值准确描述，本文拟用三参数区间灰数形式进行界定。设灰数a（？塥）=[a，，a]为三参数区间灰数，其中a≤ ≤a，a、a为区间数的下限和上限，为在此区间中取值可能性最大的数，成为区间灰数的重心。当a= =a时，三参数区间灰数退化为一个实数;当a、、a中某两个相同时，三参数区间灰数退化为区间灰数。

第三方机构对拟投资企业（Ej）针对属性（Xk）实际评价的属性值为：q ?（？塥）=[q ?， ? ，q ?]。

政府方代表Gi对拟投资企业Ej的第k个属性的期望值为：p ?（？塥）=[p ?， ? ，p ?]。

进而定义评价值与期望值的差异d ?：

d ?=d（q ?（？塥），p ?（？塥））=？坠q ?-p ?+？詛 ? - ? +（1-？坠-？詛） ? - ? ? ?（2）

其中，？坠、？詛、1-？坠-？詛是根据决策者经验、风险偏好来确定的具体权重且0≤？坠≤0.5，0.5≤？詛≤1。

（1）在此基础上，建立政府方代表的益损矩阵D=[D（q ?）]m×e×n，其中D（q ?）为政府方代表（Gi）关于拟投资企业（Ej）第k个属性的感知收益或感知损失，其计算公式如下：

D（q ?）=d ?，q ?≥p ?-d ?，q ?

i=1，2，…，m;j=1，2，…，n;k=1，2，…，e

当q ?≥p ?时，D（q ?）表示政府方代表Gi关于拟投资企业（Ej）第k个属性的感知收益;当q ?

同理，可以建立擬投资企业的益损矩阵 =[ （ ? ）]n×f×m，（ ? ）为政府方代表（Gi）的实际水平相对于拟投资企业（Ej）期望水平的收益值或损失值，也即拟投资企业（Ej）关于政府方代表（Gi）第k个属性的感知收益或感知损失，其计算公式如下：

（ ? ）= ? ， ? ≥ ? - ? ， ? ≥ ? ? ? ? （4）

i=1，2，…，m;j=1，2，…，n;l=1，2，…，f

当 ? ≥ ? 时，（ ? ）表示拟投资企业（Ej）关于政府方代表（Gi）第k个属性的感知收益;当 ? < ? 时，（ ? ）表示拟投资企业（Ej）关于政府方代表（Gi）第k个属性的感知损失。

（2）根据政府方代表（Gi）的益损矩阵，考虑其心理感知和行为偏好，依据前景理论价值函数v（x），计算政府方代表Gi的前景值v（q ?），计算公式如下：

v（q ?）=（D（q ?））α，q ?≥p ?-λ（-D（q ?））β，q ?

i=1，2，…，m;j=1，2，…，n;k=1，2，…，e

由此可建立政府方代表的前景矩阵V=[v（q ?）]m×e×n。式中α=β=0.88，λ=2.25，由Tversky通过实验方法测算而得，且较好符合行为人决策偏好。

同理，依据拟投资企业益损矩阵 =[ （ ? ）]n×f×m，可建立拟投资企业的前景矩阵 =[ （ ? ）]n×f×m。

为消除不同量纲的影响，依据前景矩阵V=[v（q ?）]m×e×n与 =[ （ ? ）]n×f×m，构建规范化前景矩阵V'=[v'（q ?）]m×e×n与 '=[ '（ ? ）]n×f×m，计算公式为：

v'（q ?）=v（q ?）/{maxv（q ?）}，i=1，2，…，m;j=1，2，…n;k=1，2，…，e ? （6）

'（ ? ）= （ ? ）/{max （ ? ）}，i=1，2，…，m;j=1，2，…n;l=1，2，…，f ? （7）

（3）计算双方满意度综合前景值。根据得到的规范化前景矩阵V'[v'（q ?）]m×e×n，计算政府方代表的满意度综合前景值Ui，j：

Ui，j=∑ ?ukv'（q ?），i=1，2，…，m;j=1，2，…n;k=1，2，…，e

（8）

根据规范化前景矩阵 '=[ '（ ? ）]n×f×m，计算拟投资企业的满意度综合前景值 j，i：

j，i=∑ ? k '（ ? ），i=1，2，…，m;j=1，2，…k;l=1，2，…，f ? （9）

Ui，j为政府方代表的满意度综合前景值， j，i为拟投资企业的满意度综合前景值，Ui，j值越大表明政府方代表的满意度越高， j，i值越大表明拟投资企业的满意度越高。

（4）构建和求解政企匹配模型。为了将双方的满意度均考虑在模型中且双方相互选择得出匹配结果，需要将双方的匹配目标融入目标规划模型中。根据获得的政府方代表满意度综合前景值Ui，j和拟投资企业的满意度综合前景值 j，i，引入0—1变量构建匹配主体前景价值最大化的匹配决策模型，其中xi，j=0表示政府方代表（Gi）与拟投资企业（Ej）未匹配，xi，j=1表示政府方代表（Gi）与拟投资企业（Ej）匹配，模型构建如下：

Max Z1=∑ ?∑ ?Ui，jxi，j ?（10a）

Max Z2=∑ ?∑ ? j，ixi，j ? ?（10b）

S.t. ?∑ ?xi，j≤1，i=1，2，…，m ? （10c）

∑ ?xi，j≤1，j=1，2，…，n ? ?（10d）

xi，j∈{0，1}，i=1，2，…，m;j=1，2，…，n

其中，式10a表示最大化政府方代表关于拟投资企业的满意度，Z1为政府方代表匹配决策目标函数，式10b表示最大化拟投资企业关于政府方代表的满意度，Z2为拟投资企业的匹配决策目标函数，式10c表示每一个政府方代表至多与一个拟投资企业匹配，式10d表示每一个拟投资企业至多与一个政府方代表匹配。考虑到PPP项目的投资回收期较长，双方承担风险较大，故匹配约束条件为一一匹配而非一对多或多对多匹配。

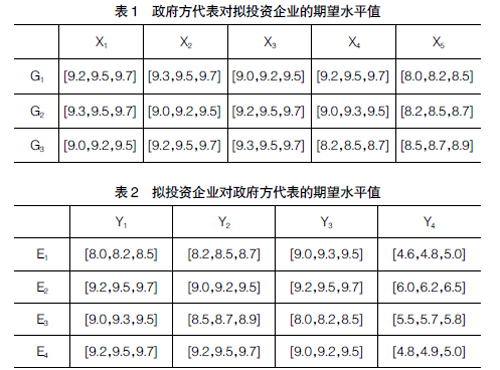
为求解目标函数，可以采用兩种解决方法。方法一，引入政企双方的拟投资股权作为政企双方的权重系数加权，进而将政企匹配决策模型转化为单目标决策模型。设wG为政府方代表的股权权重，wE为企业主体方的股权权重，满足0

MaxZ=wG∑ ?∑ ?Ui，jxi，j+wE∑

∑ ? j，ixi，j=∑ ?∑ ?（wG·Ui，j+wE j，i）xi，j

（11a）

S.t. ∑ ?xi，j≤1，i=1，2，…，m

（11b）

∑ ?xi，j≤1，j=1，2，…，m

（11c）

xi，j∈{0，1}，i=1，2，…，m;j=1，2，…，n。

令ci，j=wG·Ui，j+wE· j，i，目标函数（11a）和约束条件（11b、11c）构成的模型具有二次指派问题模型典型特征，可以将模型转化为标准指派问题模型采用匈牙利算法进行求解。方法二，在不引入权重系数的情况下，运用Lingo软件直接对双目标规划模型10a—10d编程，进而可求出匹配结果。

五、案例分析

某新区致力于建设成“世界眼光、国际标准、中国特色、高点定位”的标杆城市，其建设初期市政、交通、水利、能源、环境等基建领域重点项目对资金需求巨大，为缓解财政压力同时引进先进的科学技术综合管理优势，未来新区的基础设施项目主要采用PPP模式。现政府授权的项目代表G={G1，G2，G3}委托第三方机构从项目业绩X1、融资能力X2、技术水平X3、资信等级X4、社会责任度X5等5项指标寻找合作伙伴以促进项目落地，并按1—10的打分区间给出自身心理期望水平如表1所示，同时拟投资企业E={E1，E2，E3，E4}从政府信用Y1、政府担保Y2、投资回报率Y3、风险分担水平Y4等4项指标进行合作伙伴的选择，并给出自身心理期望水平如表2所示。

第三方机构邀请7位行业专家对拟投资企业针对指标集X={X1，X2，X3，X4，X5}进行实际评价，同时确定相对应的指标权重u=（0.2，0.3，0.3，0.1，0.1），实际评价值见表3。其次，第三方机构对政府方代表针对指标集Y={Y1，Y2，Y3，Y4}进行实际评价，实际评价值见表4所示，并确定各个指标权重为u=（0.2，0.2，0.3，0.3）。

若匹配时不考虑双方的期望水平，采用传统期望效用函数SEU=∑ρ（Xk）μ（Xk）计算效用值，其中SEU表示期望效用，ρ（Xk）表示第k个事迹所发生的概率，这里指第k个属性的权重，μ（Xk）为第k个属性的效用即实际评价值。由于实际评价值采用三参数区间灰数形式，假设根据决策者经验确定？坠=0.2，？詛=0.5，则1-？坠-？詛=0.3，根据式2，令表示心理期望水平的三参数区间灰数为0即可得出效用值，进而求出综合效用值，借鉴10a—10d构建效用值最大化的双目标规划模型，运用Lingo 11.0软件编程得出以下6种匹配结果。

x11=1，x12=0，x13=0，x14=0 x11=1，x12=0，x13=0，x14=0

x21=0，x22=0，x23=1，x24=0 x21=0，x22=0，x23=0，x24=1

x31=1，x32=0，x33=0，x34=1 x31=0，x32=0，x33=1，x34=0

x11=0，x12=0，x13=1，x14=0 x11=0，x12=0，x13=0，x14=1

x21=1，x22=0，x23=0，x24=0 x21=1，x22=0，x23=0，x24=0

x31=0，x32=0，x33=0，x34=0 x31=0，x32=0，x33=1，x34=0

x11=0，x12=0，x13=1，x14=0 x11=0，x12=0，x13=0，x14=1

x21=0，x22=0，x23=0，x24=1 x21=0，x22=0，x23=1，x24=0

x31=1，x32=0，x33=0，x34=0 x31=1，x32=0，x33=0，x34=0

若考虑双方的期望水平，则根据式2计算表3和表4中实际评价值和期望水平的差异，得出益损值构建益损矩阵，并由此根据式5计算出政企双方的前景决策矩阵，如表5和表6所示。

为去除量纲的影响，根据式6、式7对得到的前景值进行无量纲化处理，并用式8“Ui，j=∑ ?ukv'（q ?）”计算政府方代表的满意度综合前景值，用式9“ j，i=∑ ? k '（q ?）”计算拟投资企业的满意度综合前景值。最后根据10a—10d构建政企匹配决策模型。

Max Z1=∑ ?∑ ?Ui，jxi，j

Max Z2=∑ ?∑ ? j，ixi，j

S.t. ∑ ?xi，j≤1，i=1，2，3

∑ ?xi，j≤1，j=1，2，3

Xi，j∈{0，1}，i=1，2，3;j=1，2，…，4

同样运用Lingo 11.0软件包进行编程求解，得出匹配结果为：

x11=0，x12=0，x13=1，x14=0

x21=0，x22=0，x23=0，x24=1

x31=0，x32=1，x33=0，x34=0

通过两种结果的对比可知，是否考虑心理期望对匹配结果有着重要影响。在运用期望效用理论和前景理论分别对案例进行模型构建和求解的过程中，区别在于是否考虑了双方的心理期望，从而导致匹配结果不同。基于效用最大化构建的模型在满足约束条件的情况下得到了6种可能的匹配结果：G1与E1匹配，G2与E3匹配，G3与E4;G1与E1匹配，G2与E4匹配，G3与E3;G1与E3匹配，G2与E1匹配，G3与E4;G1与E4匹配，G2与E1匹配，G3与E3;G3与E1匹配，G2与E4匹配，G3与E1;G1与E4匹配，G2与E3匹配，G3与E1匹配。在可能存在的匹配对中，观察到E2企业均不在任意一对匹配结果中。追根溯源可知，E2企业的综合效用值在四个拟投资企业中最低，其综合效用值为9.17。基于前景价值最大化构建的匹配模型得到的匹配结果为：G1与E3匹配，G2与E4匹配，G3与E2为匹配。两种模型在满足同样的约束条件下，前者得到了6种均可能出现的匹配结果，后者得出了一对唯一的匹配结果，而在后者得出的匹配结果中，E2企业存在于匹配对中。尽管通过第三方机构中得出E2企业的综合效用值最低，但在匹配决策过程中将政府方代表的心理期望作为内生变量时，E2企业由最初的落选企业成为了匹配成功的合作伙伴。政府方代表和拟投资企业处在的社会环境中使其符合有限理性人特征，而在决策过程中考虑双方的心理期望，并设立心理期望为参照点进行模型的构建、求解与应用，进而得出最优匹配结果是科学合理的。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。