《挂钩单一标的的自动敲入敲出期权结构的定价研究》-管理学论文，管理论文-论文范文参考-科学狗论文网

标题

挂钩单一标的的自动敲入敲出期权结构的定价研究

范文

潘琪

摘要：研究双障碍期权定价问题，主要是在双常数敲出边界的期权定价的基础上，研究上敲出边界是常数，下敲入边界是一个偏微分方程形式的随时间变化的不定边界的奇异期权的定价问题，提出解决该种期权的定价模型。该种期权是当前利用期权规避风险的行之有效的方法，能够有效的应对市场价格的波动。

关键词：双障碍期权;敲入敲出;偏微分方程;Black-Scholes模型

中图分类号：F23 文献标识码：A doi：10.19311/j.cnki.1672-3198.2019.34.052

0 引言

全球金融市场快速发展，投资者对冲风险和套期保值的需求日益增长，各种金融衍生产品应运而生。期权作为金融衍生产品的一种，受到投资者的青睐。障碍期权是指在其生效过程中受到一定限制的期权，其目的是把投资者的收益或者损失控制在一定范围之内。一般关于障碍期权的讨论往往只涉及比较简单的情况，即期权障碍是恒定不变的。但期权障碍是会随时间而变化的，在此情况下的障碍期权的定价则是金融研究的关键问题。障碍期权一般分为两类，即敲入期权和敲出期权。在市场利率波动的情况下，例如对于一个看涨的标的物，投资者购买现货可能要承担标的物价格下降的风险，为了规避这种风险，投资者更倾向于选择支付手续费购买看涨期权产品。

1 模型定价

Black，Scholes[1]和Merton[2]创造性地提出了Black-Scholes 模型。该模型是期权定价理论的重要内容之一，是金融工程研究的基础。他们在期权定价模型方面基础性的工作促进了衍生产品的开发和研究，使金融工程得到飞跃的发展。

1.1 Black-Scholes期权定价公式

Black-Scholes的期权定价理论假设条件如下：（1）标的资产价格变动比例遵循一般化的维纳过程，该假定等价于标的资产价格服从对数正态分布;（2）允许使用全部所得卖空衍生资产;（3）没有交易费用和税收;（4）不存在无风险套利机会;（5）无风险利率为常数且对所有到期日都相同。

St表示标的资产在时刻t的价格;K表示期权的敲定价格;T表示期权的到期日;t表示目前期权所处的时刻，τ=T-t表示期权的有效时间;B（τ）=Be-γT表示障碍水平，其中B，γ为常数，B（τ）随τ的改变而呈指数改变。

其中，N（x）表示标准正态分布N（0，1）的概率值;假设股票的连续收益满足布朗运动Wt（布朗运动：独立平稳增量的随机过程，每个区间上的增量满足正态分布。即股票价格满足几何布朗运动。）但是Black-Scholes 模型在实际应用中存在着许多局限性，例如：利率和波动率都是不随时间变化的常数，这和现实相差较大。

1.2 Black-Scholes微分方程

资产价格满足如下随机微分方程：

V代表期权的价格，S代表股票现价，Δ表示购买股票的份额，r表示无风险利率，Bt表示一维布朗运动，μ表示期望回报率，σ表示波动率，μ和σ是常数。在t时刻构造Π=V-ΔS的投资组合。

1.3 障碍期权定价

障碍期权分为如下八种情况：

期权价格满足的偏微分方程其实是普通障碍期权的定价问题，可归结为一个求解抛物型偏微分方程的問题。在定解范围内，所有的障碍期权都满足B-S方程：

（1）产品的期限为12个月：每个月的敲出观察日，如果中证500指数价格高过敲出界限100%，产品提前结束，客户收取票息（年化14%）。

（2）如果产品到期日还没有敲出，现金流会是如下两种情况：

①产品周期内没有敲入（中证500指数没有低过86%），客户收取红利票息14%。

②产品周期内发生敲入事件（中证500价格曾低过86%），客户出现亏损：

（1-期末价格/期初价格）*本金

定价假设：中证500期初价格=4000;利率=0;分红率=0;Flat vol surface=11%;中证500指数遵循指数正态过程。

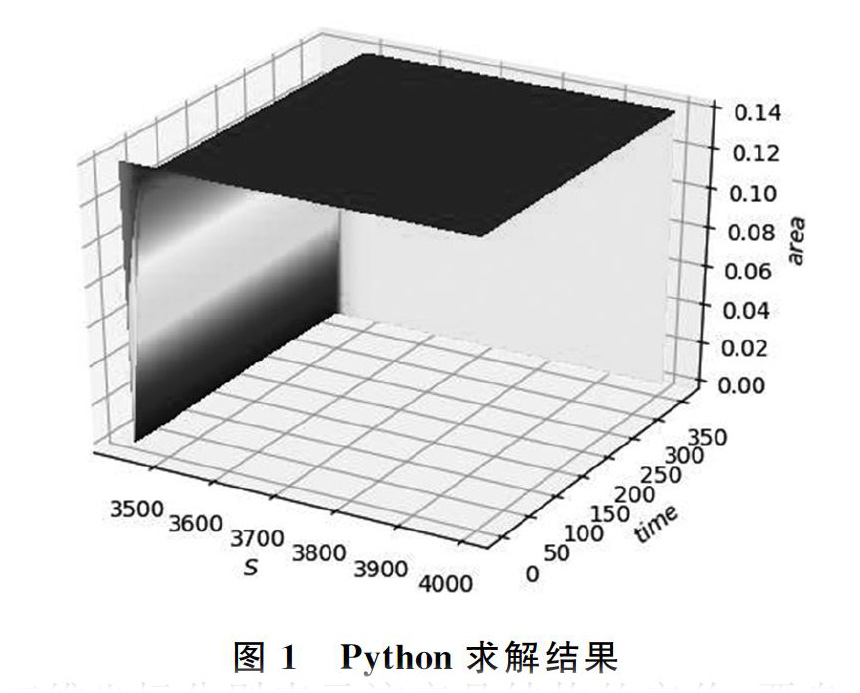
将各指标代入上文的求解过程，用Python求解可得如图1结果。

三维坐标分别表示该产品结构的定价、票息和时间。本文将该障碍期权看成下降敲入期权和上升敲出期权的组合，分开求解绘制成如上的价格过程。

产品化结构已经变得越来越流行，而这些产品可以分化成障碍期权的组合形式，其中心思想是小概率事件的应用，以保障金融市场中买卖双方的利益，为风险厌恶者规避风险。

参考文献

[1]Black F，Scholes M.The pricing of options and corporate liabilities[J].Journal of Political Economy，1973，（81）：637-654.

[2]Merton R.The theory of rational option pricing[J].The Bell Journal of Economic Management Science，1973，（4）：141-183.

[3]Hull J，White A.The pricing of options on assets with stochastic volatilities[J].Journal of Finance，1987，（42）：281-300.

[4]刘国买，邹捷中.双边敲出障碍期权的定价模型[J].经济数学，2003，20（04）：31-37.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。