《新课标下高中数学教材例题设置的难度研究》-教育论文，科学教育论文-论文范文参考-科学狗论文网

标题

新课标下高中数学教材例题设置的难度研究

范文

刘佳李琪苏淑华皮帅玲

摘要数学教材是将教育理念、课程标准转化为实际教学的主要载体，而教材中的例题是把数学知识、技能、思想和方法联系起来的纽带。以北师大版平面向量的例題为例分析高中数学难度情况。研究发现，北师大版平面向量的例题设置在计算和推理水平难度较大，在背景和认知水平难度较低，同时也体现了对数学学科核心素养的考查。

关键词课程标准高中数学教材例题青浦模型

中图分类号：G424?????????????????????????????????????文献标识码：A ???DOI：10.16400/j.cnki.kjdkz.2019.07.065

A?Study?on?the?Difficulty?of?Setting?Examples?in?Senior?Mathematics

Textbooks?under?the?New?Curriculum?Standard

——Take?plane?vector?as?an?example

LIU?Jia，?LI?Qi，?SU?Shuhua，?PI?Shuailing

（Fuzhou?Normal?College?of?ECUT，?Fuzhou，?Jiangxi?344000）

Abstract Mathematics?textbooks?are?the?main?carriers?of?transforming?educational?concepts?and?curriculum?standards?into?practical?teaching.?Examples?in?the?textbooks?are?the?links?between?mathematical?knowledge，?skills，?ideas?and?methods.?Taking?the?example?of?plane?vectors?in?the?edition?of?Beijing?Normal?University?as?an?example，?this?paper?analyses?the?difficulty?of?high?school?mathematics.?It?is?found?that?the?example?setting?of?plane?vectors?in?the?edition?of?Beijing?Normal?University?is?more?difficult?in?calculation?and?reasoning，?less?difficult?in?background?and?cognitive?level，?and?also?reflects?the?examination?of?the?core?literacy?of?mathematics.

Keywords curriculum?standard;?senior?mathematics?textbooks;?examples;?Qingpu?Model

1?研究背景

2018年1月正式颁布了新修订的《普通高中数学课程标准（2017年版）》，新课标明确提出育人的核心目标就是培养学科素养。数学学科素养包括：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析。这些数学学科核心素养即相对独立，又相互交融，是一个有机的整体。数学核心素养可以通过四个方面得以体现，包括：情境与问题、知识与技能、思维与表达和交流与反思。

如何对教材进行定量和定性研究，以期更好的服务师生，成为许多学者的研究目标，而数学例题又是有效教学的关键，以往的研究更多的是对教材的比较研究，而且大多是对习题的难度研究，对例题的研究相对较少。例如史宁中等建立课程难度模型，鲍建生利用综合难度模型对教材习题难度进行了研究，来考察不同版本的难度情况。[1]

例题教学是数学教学的重要组成部分，是抽象的概念、定理、公式和具体实践之间的桥梁，是使学生的数学知识转化为数学能力，形成数学核心素养的重要环节，近年来随着数学课程改革的不断推进，在例题设置上也需要开始转变，在这样的背景下，以北师大版平面向量的例题为例，通过用青浦模型对高中数学例题的综合难度分析，探究例题对数学科学素养的考察情况。

2?例题难度分析

就目前教材研究分析而言，青浦模型还是一个相对比较客观，操作性强，可量化，能够反映教材难度水平的一个测量工具，而且还能体现完整的数学活动过程。通过青浦模型对例题的难度分析，可以体现情境与问题、知识与技能、思维与表达和交流与反思四个方面考察的水平层次，进而体现数学学科核心素养考察情况。

2.1?背景维度分析

数学问题的“背景”因素划分为四个不同的层次水平：无背景、个人生活、公共常识和科学情境。在北师大版平面向量例题中，每道题都有其相应的背景，以例题2为例。[2]（P75，例2）

难度分析：该题从生活实际问题出发，考察了平面向量的知识，需要学生掌握一定的预备知识，具有一定的数学抽象的能力。解答该题首先将船港问题抽象成平面向，根据向量的关系得到。该题背景水平为2，认知水平为3，计算水平为4，推理水平为2，知识水平为3。这个例题其实是以轮船行驶问题为背景，要求学生在真实情境中将具体问题抽象成数学问题，即体现数学抽象素养的内涵，同时对数学建模、数学运算作出相应的要求。

2.2?认知水平

认知水平可以分为四个层次：计算、概念、领会和分析。教材中的例题在不同层次考察认知水平，以例题2为例[2]（P83，例2）

难度分析：该例题从图像出发，考察平面向量共线性质的判定依据需要学生对向量共线概念，向量的几何运算知识的掌握，运用数形结合的思想解决数学问题，具有一定的数学直观想象素养。从题中得到。该题的背景水平为1，认知水平为1，计算水平3，推理水平为2，知识水平为1。这道平面向量共线判定問题，要求学生能在认知水平上领会概念、性质的内涵并能灵活运用，同时也考察数学直观想象素养。

2.3?运算

根据鲍建生的青浦模型，数学题里的运算水平可以分为以下四个层次：无运算、数值计算、简单的符号运算和复杂符号运算。以例题5为例[2]（P84，例题5）

难度分析：本题从图形出发，考察平面向量加减运算。根据向量的几何意义，得到：。该题的背景水平为1，认知水平为1，计算水平为3，推理水平为2，知识水平为2。该题需要学生掌握平面向量的几何意义和线性运算，灵活运用平面向量的运算，具有一定的数学运算素养。

2.4?推理

根据鲍建生的综合难度青浦模型，推理维度可分为三个水平层次：无推理、简单推理和复杂推理。推理的一般形式为：“因为…所以…”以例题3为例[2]（P94，例题3）

难度分析：该题从菱形对角线垂直证明出发，考察平面向量垂直性质，则向量相乘为0的知识点。解答该题需要证明：。该题的背景水平为1，认知水平为4，计算水平为3，推理水平为2，知识点水平为3。该题需要学生用逆向思维从结果反推条件，学会用向量去解决几何问题，对平面向量的乘法运算熟练运用，需要具有一定的逻辑推理素养。

2.5?知识含量

知识含量就是一道例题中所含知识点的个数，知识含量分为三个水平层次：一个知识点、两个知识点和三个或三个以上知识点。以例题5为例[2]（P78，例题5）

难度分析：本题从数学计算出发，考察向量的模的概念和计算。解答该题的关键是：即。该题的背景水平为1，认知水平为3，计算水平为4，推理水平为2，知识水平为3。该题需要学生掌握向量模的概念和计算，即其几何意义，运用数形结合的思想，对问题进行深度解析、判断、计算，具有一定的数学逻辑推理和直观想象素养。

3?综合难度汇总分析

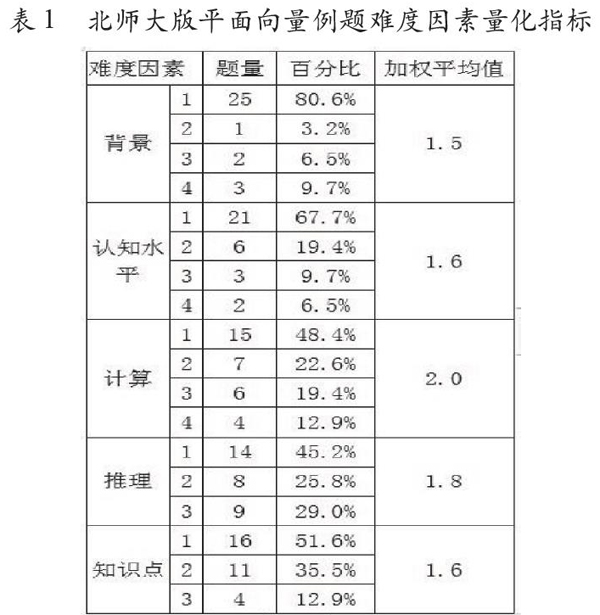
为了了解高中数学例题设置难度情况，对北师大版平面向量共31道例题5个维度进行详细的分析，根据因素水平权重，利用以下公式可以计算例题在每个因素的加权平均值：

其中，d_{i}表示第i个难度因素上的加权平均值，d_{ij}表示第i个难度因素的第j个水平的权重，这里直接采用等级权重，即d_{ij}=j;n_{ij}则表示这套教科书例题中属于第i个难度因素的第j个水平的题目的个数，则n是样本总数。显然，对如何i，都有。

汇总如表1。通过分析表1中的数据可以发现，例题在不同维度不同水平均有设置，能够体现数学学习的活动过程，间接体现数学学科核心素养。例题在每个维度的低水平所占比例高达一半以上，特别是背景维度和认知水平，分别高达80.6%和67.7%;而且各个维度的加权平均值存在差异，其中计算和推理维度的加权平均值较大，分别为2.0和1.8，明显高于其他维度，而背景和认知水平的加权平均值较低，说明我们现有的北师大版教材比较注重数学计算和推理，偏向对基本知识和技能的学习和培养，但对背景和认知水平设置偏少，对基本经验和基本过程设计甚少。通过第二节的难度因素分析，不难发现，有些例题在各维度都在一个比较高的水平，综合体现了数学学科核心素养，如北师大版平面向量例题3、4、5、30、31等。

4?结论与建议

通过对北师大版高中数学教材“平面向量”例题的难度分析，结合数学核心素养的考察，研究发现：现有北师大版高中数学平面向量例题设置比较全面，不仅考察了学生的基本知识和基本技能，也考察了学生的基本思想和基本经验。例题以学科知识为载体，以数学能力为核心，对各维度进行了考察，但是目前的例题整体设置偏向对数学计算和推理的考察，而对背景和认知水平的考察较少。

数学例题作为数学教学过程中的关键一环，肩负着服务师生、提高教学效率的重要使命，对新课标的目标实现发挥着至关重要的作用，为了改善高中数学例题设置情况，基于上述分析提出建议：对于高中数学新课标的育人目标要求以数学学科核心素养为导向，教材例题的设置要以学生的认知水平为基础，发展学生数学学科核心素养为宗旨。随着时代的迅猛发展，新兴技术也在高速发展，为了更好的?适应未来的工作与生活，高中学生需要具备数学建模与数学探究能力，建议在例题设置背景更加情境化，例题的开放性可以有所增强，把数学学科核心素养融入到具体的知识内容和思想方法中。

参考文献

[1] 张卢西子.中法两国高中数学教材例题的综合难度比较[D].华东师范大学，2017：11-12.

[2] 普通高中课程标准实验教科书?数学必修4.北京师范大学出版社：69-102.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。