《初中数学二次函数的教学策略》-教育论文，科学教育论文-论文范文参考-科学狗论文网

标题

初中数学二次函数的教学策略

范文

刘卫国

摘要：二次函数部分知识是初中数学的重要组成部分，也是中考数学的热门考点，对学生以后的数学学习具有重要的基础作用《义务教育数学课程标准（。2011年版）》明确提出，学生通过二次函数的学习能够体会二次函数的生活意义，能够观察二次函数的图像和理解二次函数的性质，并且能够实现二次函数与一元二次方程的转化，完成求解。函数部分知识较为抽象，介于初等数学和高等数学之间，学生理解起来难度较大，成为了很多学生初中数学学习的难点。如何设计二次函数部分课堂教学，提高二次函数部分知识课堂教学效果，是众多一线初中数学教师研究的重要课题。

关键词：初中;数学;高效课堂

中图分类号：G4文献标识码：A文章编号：（2021）-04-405

二次函数是初中数学需要重点掌握的内容，包括函数的性质、图像及应用，其中二次函数的应用是新课改的主要侧重点，可充分体现学以致用的理念.中考对其的考查主要集中在二次函数与数学建模融合，利用二次函数模型研究实际问题.解析的一般思路可概括为“数学建模，性质剖析”，即首先结合数学知识根据题设条件构造二次函数模型，然后利用二次函数的性质解决问题.在建模过程中，需要充分结合实际问题的特点，简化模型，解析时利用函数性质准确求解，下面举例探析。

一、初中数学二次函数部分知识概述

初中数学二次函数部分知识的教学主要分为二次函数概念教学、二次函数图像与性质教学、二次函数解析式教学和二次函数综合应用教学几个部分。二次函数部分知识主要出现在高年级的数学教材中，是中考数学的必考点之一，它常常作为中考试题的压轴题出现，对学生的数学考试起着决定性的作用。初中学习的二次函数知识不仅是初中阶段的重点，而且是在为高中乃至以后的数学学习奠定基础，例如，圆锥曲线、极限、微积分等部分知识都涉及二次函数的相关知识。

二、初中数学二次函数部分知识教学策略探究

（一）二次函数概念教学策略

二次函数概念教学是二次函数部分教学的重点，是今后二次函数顺利教学的重要保障。首先，要根据学生的认知特点，注重对学生概念形成过程的教学。在教学过程中，部分教师会直接给出二次函数的概念让学生记忆，然后通过练习帮助学生理解。由于学生的抽象思维能力还不够，对二次函数这类抽象性较强的问题理解起来难度较大，外加是第一次接触二次函数的相关知识，不可能通过教师的几句描述就能够理解，这就导致学生对于二次函数y=ax2+bx+c的理解仅仅停留在感性认识上。教师在二次函数概念的教学中，可以通过创设相关的问题情境来引导学生认识二次函数概念的形成过程。例如，教师多列出几个与学生生活实践相关的问题，让学生来列式，然后观察这些式子的特征，再总结二次函数的定义，这样学生能够更好地理解二次函数的概念。其次，通过典型例题的辨析，帮助学生加深对二次函数概念的理解。例如，教师可以选择需要进一步转化，才能够进行二次函数辨析的式子，来帮助学生加深对二次函数概念的理解。

（二）二次函数图像与性质教学策略

首先，循序渐进、由易到难对学生进行教学.在开始接触二次函数图像的时候，教师可以从y=x2的图像入手，由于它的图像相对简单，学生理解起来难度较小，学生只需要知道二次函数的图像是一条平滑的抛物线即可.然后引导学生观察二次项系数不同的二次函数图像的特点，观察它们的开口大小、开口方向等，总结二次项系数对二次函数图像变化的影响.然后在这个基础上加深对二次函数图像的探究，让学生观察常数项不同的情况下对二次函数图像的影响，总结一次项系数和常数项对二次函数图像的影响.通过这样循序渐进拆分式的学习，让学生对二次函数的图像有进一步的认识.其次，培养学生的作图能力，让学生在作图的过程中体验二次函数图像的性质.在二次函数教学初期，借助一次函数和反比例函数教学中的描点法指导学生画图，通过学生亲自动手绘制，帮助学生加深对二次函数的理解.然后引导学生观察绘制的二次函数图像的特点，从二次函数图像性质的角度出发再次绘制二次函数的图像，在这个过程中，学生先绘制图像的一半，再根据二次函数图像的特性绘制另一半，这样学生在绘制二次函数图像的同时加深了对二次函数图像性质的理解。

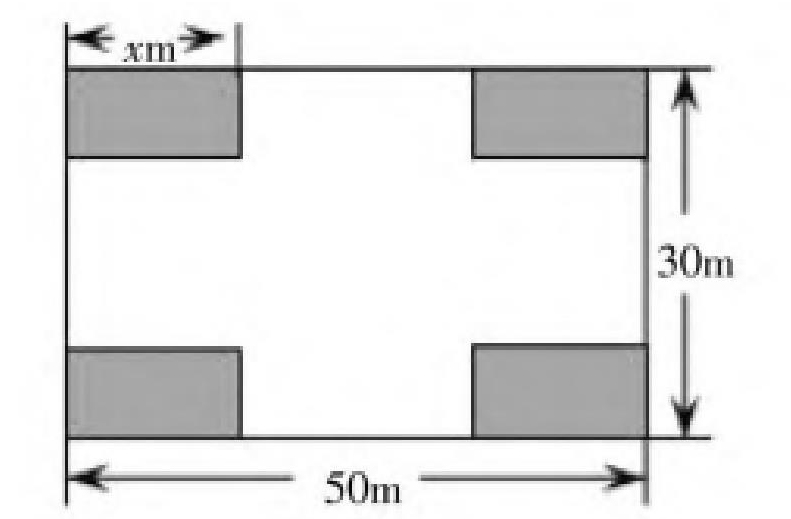
比如最值问题分析：利用二次函数建立数学模型可用于实际问题中的最值分析，建模过程与“临界点讨论”型问题有所不同，不具有曲线类比性，“最值问题分析”型更侧重挖掘变量之间的函数关系，如边长与面积之间的关系、定价与利润之间的关系等.因此在数学建模过程中，应注重挖掘变量之问的关系，利用关系构造模型，而性质剖析阶段则应侧重提取定义域，适度变形解析式，关注最值点，包括顶点、端点。例：某小区计划将一块长50m、宽30m的矩形空地改建成广场，设计图如图所示.其中阴影区表示绿化区（全等的矩形），空白区则为活动区，要求：四周的4个出口宽度一致，均不小于14m，不大于26m.设绿化区的长边为戈m，活动区的面积为ym2

（1）直接写m：①用含有戈的式子表示四周出口的宽度;②y与戈的函数关系式，以及戈的取值范围.（2）试求活动区的最大面积.（3）预计活动区的造价为50元/m2，绿化区造价为40元/m2，若投资不超过72000元，当x为整数时，共有几套建造方案。

（三）二次函数综合应用教学策略

首先，提高学生的数学阅读能力，这是学生解决函数综合应用问题的基础.如果学生的数学阅读能力较差，就会在题目的分析上出现问题，就会造成解题错误.在教学过程中，为了提高学生的数学阅读能力，教師可以有计划地对学生开展数学材料阅读训练.在与学生一起分析试题的时候，要注重对学生问题分析的引导，对于其中的关键术语要做好解释，培养学生对题目中原有条件进行转化的能力.其次，在教学中向学生

渗透建模思想和数形结合思想.教师可通过设计一些简单的建模问题帮助学生树立建模意识，如最大利润、最大面积、最优方案等问题.通过这些问题的锻炼，让学生从中领悟解题的精髓，学会建模的方法，这样学生再遇到二次函数综合应用题的时候，就能够快速地将复杂的问题简单化，才能够实现高效解题.另外，二次函数的很多知识与几何密切联系，数形结合思想能够帮助学生更加直观地完成二次函数问题的求解.因此，在二次函数的教学中，教师要设置一些巧用数形结合思想来解决的问题，训练学生利用数形结合思想解题的能力。

参考文献

[1]陈仙.二次函数的概念教学在提高学生数学核心素养中的应用[J].黑龙江科学，2020，11（21）：60-61.

[2]李俊.初中数学“二次函数”的教学策略研究[J].科学咨询（教育科研），2020（11）：244.

[3]龙旭梅.初中数学的函数教学方法经验谈[C].福建省商贸协会、厦门市新课改课题小组.华南教育信息化研究经验交流会论文汇编（七）.福建省商贸协会、厦门市新课改课题小组：福建省商贸协会，2020：119-123.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。