《探析转化思想在初中数学教学中的应用》-教育论文，科学教育论文-论文范文参考-科学狗论文网

标题

探析转化思想在初中数学教学中的应用

范文

吕淑娟

摘要：为了让学生对数学有一个更清晰的认识，老师应该将数学思想作为数学教学精准提炼的方式方法。为了让学生在初中学习过程中更加顺利，老师首先应该将教材当中原有所涉及的转化思想分散到数学学习当中，然后再选取题目中包含的转化思想，最后让学生形成自我的转化思想并且能够熟练的运用。因此笔者将结合数学思想当中的转化思想，并将此运用到初中数学教育当中，为初中数学老师提供有效的意见和建议。

关键词：基础教材;题目延伸;转化运用

中图分类号：G4 文献标识码：A 文章编号：（2021）-18-

本文所讲到的转化思想，通常是将学生未知的问题转化成已知的问题，将过于抽象的现象转化为具体的现象，将实际生活的问题转化成数学问题进行解答。转化思想是数学教育中必不可少的一部分，更是对学生提高解题能力的关键所在。因此老师在进行数学教育的过程当中应该有意识的向学生输入转化思想理念，并且在数学教育过程中进行转化思想的频繁应用。

一、利用基础教材，分散运用到数学学习中

在基础教材的教学过程当中，作为老师和学生最应该关注的就是运算能力，在数学学习的过程当中，如果老师为了让学生学会计算而计算，学生单纯是为了完成任务而计算，那么老师想要将数学思维融入到课堂当中将非常困难，并且无法让学生学会避重就轻，学生难以换个角度思考问题的话，一定在学习过程当中会得不偿失。这个时候，若结合基础教材涉及的转化思想运用到平时教学过程当中，一定会起到事半功倍的效果。

例如，“数与式”这一部分的学习中就随处体现了转化思想，如：有理数的减法就是利用“相反数”这一概念，将减法转换成加法来运算，从而得到一个减法的原则：减去一个数等于加上这个数的相反数。通过这样一种转化方式让加减法得到了一个统一。并且有理数的除法也是通过“倒数”的基本规则来进行转化而去除的，同时也得到了除法法则：除以一个不为零的数等于乘以这个数的倒数。从而使得乘除法得到了统一。这一概念的运算就是涉及在课本基础只是当中，想要利用减法原则和除法原则就必须熟悉课程基本内容，只有将其中的基础知识进行掌握和运用，才可以运用转化思想解决所遇到的数学问题。

数是一个抽象的概念，数学当中的问题都是一些抽象的问题，因此老师学要将这些抽象的问题转化为直观的问题进行解释，让学生通过学习课本基础知识的学习能够熟练掌握知识节点，进而利用这些知识节点融入未来数学学习和计算当中，将学生不知道怎么解决的问题转化为易懂的平时问题进行解决，这会让初中数学教学更加顺畅。

二、选取代表题目，从经典题目中挑选知识点

老师通过学生所做的题目进行转化思想的提取，不仅将题目进行了讲解和分析，还向学生传授了转化思想。老师布置作业实际上就是让学生进行一个不断的尝试，学生在自主的尝试运用当中主动参与知识的實践，不再单一的听取老师的讲解和教材的梳理，将旧的知识转化为自己的新知识，并且建立一个属于自己新的知识构架，进而主动地掌握数学转化思维，提高数学能力。

例如，其中一个问题：一跳蚤在一直线上从O点开始，第一次向右跳1个单位，紧接着向左跳2个单位，第3次向右跳3个单位，第4次向左跳4个单位，……，依此规律跳下去，当它跳第100次落下时，落点处离0点的距离是_单位。

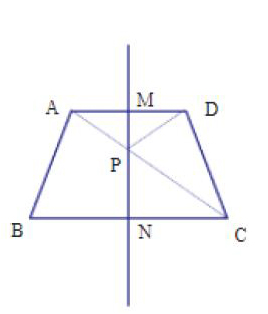
第二个问题.如图，在梯形ABCD中，AD//BC，AB=CD=AD=1，∠B =60°，直线MN为梯形的对称轴，P为MN上一点，那么PC+PD的最小值是_。这道题的分析：利用轴对称把PC+PD的最小值转化为两点间距离，因为两点间线段最短，所以连.接AC交MN于P点，再连接PD，PD+PC= AC，求出AC长即可。

这两个问题的解决都将转化思想进行渗透和融合，老师让学生学会从题目中提取关键信息进行题目的简化，并且结合具体的问题进行解决会让学生对转化思想有一个更清晰的认识。转化思想能够让学生更容易的解决问题，同时锻炼了学生的思维能力，想要接触这道题目的答案就一定要变化固定的思维，跳出自己的舒适圈才可以有一个更广阔的视野，让数学问题的解决迎刃而解。

三、形成自我思维能力，熟练运用

所有的学习过程都是反复无常的，每个学生都是在成功与失败当中不断进步，在失败当中获取经验，并且达到自我实现。转化法能够让学生在数学学习过程中体会到更大的成就感。因此，学生自己要不断加强转化法在数学学习中的运用，构建一个新的知识体系，让学生通过自己所设置的知识体系进行学习，主动的理解和掌握转化思维，化生疏为熟悉。

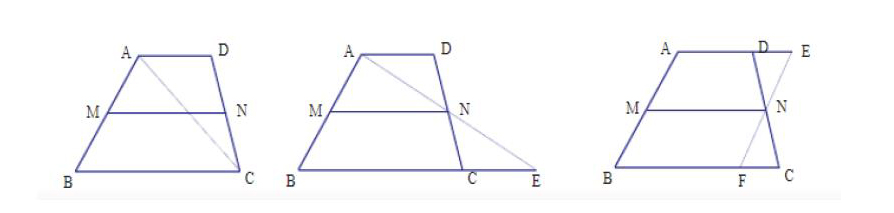
例如：在进行梯形的中位线的教学当中，老师应该让学生掌握的一个方法就是通过连线或者补割让梯形转化为三角形。在此之前老师不应该进行课程的教学，首先鼓励学生进行小组探究，自己总结得出解决办法：第一个就是连接梯形的对角线得到一个或者几个三角形;第二个就是利用补割的办法，利用全等三角形将梯形转化成三角形;最后就是利用三角形的全等将梯形转变成平行四边形。

这三种方法的思考是建立在学生小组各自独立思考的基础之上，在学生未来进行这一类题的计算时，当做题没有思路的时候就一定会联系起小组讨论的过程，紧接着想起大家讨论出来的方法，这不为是一个很好的实践办法。

通过以上三种方法的比较，可以让学生更为直观的认识到后面两种方法更容易得出梯形的中位线，这样一种教学方式不仅完成了教学内容，还让学生从自己的总结方法中获得自信。这样一种学习模式能够让学生形成属于自己的学习思维，并且能够更好地促进他们在接下来的学习当中进行熟练地运用。

转化思维是初中数学学习中非常广泛运用的一种学习方法思维，转化思想实际上就是学生在进行解题过程当中的简便方法，在教学中，老师有意识的通过基础课本知识挖掘转化思维，然后在题目中提取具有代表性的转化思维题目，最后培养起学生转化思想的应用，这一系列的办法不但让学生更容易解决数学问题，还可以通过转化思维解决利用多种方法解决同一个问题。转化思维在初中数学中的应用实际上就是从课本到题目最后进入学生自己的思维过程当中，让学生在数学学习过程中更加容易。

参考文献

[1]许阳.浅谈数形结合思想在初中数学教学中的应用[J].安徽教育科研，2021（09）：56-57.

[2]吕相春.数学化思想在初中数学教学中的拓展应用分析[J].中学生数理化（教与学），2021（03）：78.

[3]于霞.转化思想在小学数学教学中的应用[J].陕西教育（教学版），2021（03）：58.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。