《数学教学精准追问时机的选择》-教育论文，小学教育论文-论文范文参考-科学狗论文网

标题

数学教学精准追问时机的选择

范文

汪国祥

摘要小学数学教学中精准追问应关注的地方很多，其中把握追问的时机是关键。一般在学生没有完全理解时、学生理解出现问题时、学生已经理解本质时等节点追问能取得事半功倍的效果。

关键词追问时机理解本质

追问是上一个提问的延伸和拓展，是为了帮助学生弄懂、弄通某一内容或问题，在一问之后再次补充和深化、穷追不舍.直到学生能正确解答、深入理解、沟通联系。追问要精准，精准追问会使学生对问题的认识由模糊走向清晰，理解由片面走向全面，思维由浅表走向深入，课堂对话也由单一走向丰富，让学生既知其一又知其二，既知其然又知其所以然。小学数学教学中精准追问有很多需要关注的地方，精准的追问时机就是非常重要的一个方面，一般可以在以下节点进行追问。

一、学生没有完全理解时

1.学生感觉没有问题时

有些内容表面看似乎比较简单，学生会有一种一学就会的感觉。刚开始学就感觉没有问题，他们接下来就不会很认真地学。遇到这种情况，很容易出现对新知识理解不够深刻的情况，需要教师通过追问，让学生用变式判断等方法理解学习内容。如学习人教版《数学》四年级下册“三角形的认识”一课，学生知道三角形是怎样一种图形后，教师先后旋转同一个三角形，改变其中一条边的长度（仍是j角形），让学生说说这个图形还是三角形吗，为什么？通过变式判断并说明理由，让学生明白“由3条线段围成的图形（每相邻两条线段的端点相连）叫做三角形”，只要符合这些条件的图形都是三角形，跟三角形的位置和形状无关。教师继续追问：是不是三条线段一定可以围成三角形呢？讓学生通过拼三角形的活动认识到“如果短的两条线段的长度和大于第三条线段就可以围成三角形，否则不能围成三角形”。

2.学生理解似懂非懂时

有些内容理解起来不是很容易，表面上看学生已经理解了，但实质上并没有完全理解，处在似懂非懂的状态。遇到这种情况，很容易出现对新知识一知半解的情况，需要教师通过追问，通过结合实例说说等方法真正理解。如学习人教版《数学》二年级上册“认识几时几分”一课，刚开始学生就已经会认记6时半和6时20分这些相对比较简单的时间，但不太清楚是怎么看时间的，教师可以追问：分针和时针分别在什么位置？然后先让学生拨几个时间让其他学生认记，并说说是怎么认记的，再让学生说几个时间让其他学生在钟面上拨出来，并说说是怎么拨的。通过举例说明是怎么认记的，让学生明白拨或者看时间时需要弄清楚时针和分针的位置，分针走过几小格就是几分，时针过了几就是几时多，过了多少由分针走过的时间决定。

3.学生表达不够清晰时

有些内容理解起来难度不是很大，学生似乎也已经理解主要意思，但就是表达不够清晰，导致学生想说却说不清楚。遇到这种情况，很容易出现对新知识理解的模棱两可，需要教师通过追问，让学生用不断表述的方式慢慢理清。如学习人教版《数学》五年级下册“质数和合数”一课，学生知道什么样的数是质数后，举例说说什么样的数是合数，学生A说：4是合数，因为4的因数有1、2、4三个，学生B说：6是合数，因为6的因数除了l和它本身还有2和3，教师追问：你们认为哪种表述更好？学生都认为是后者表述更好，但具体好在哪里大家都说不清楚。于是，教师让学生不断地变换表述方式，有学生认为，说清楚了6的因数除l和它本身之外还有2和3，有学生认为，说出了与质数的不同，有学生认为，不光说出了与质数的不同，还说出了合数的特点。

二、学生理解出现问题时

1.学生出现意见分歧时

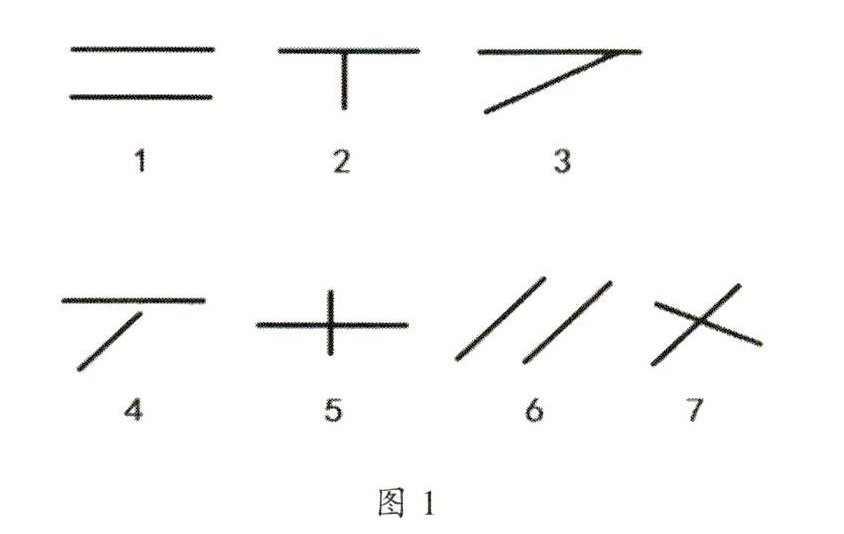
由于学生的知识基础、学习能力和思维水平各不相同，他们在理解某些知识时自然会出现意见分歧，常常表现为谁都说服不了谁。遇到这种情况，教师可以追问，让学生借助辩论逐步达成共识。如学习人教版《数学》四年级上册“两条直线的位置关系”一课，学生在给图1中的图形按照两条直线的位置关系分类时出现了分歧。A类学生认为1、4、6一类，2、3、5、7一类;B类学生认为1、4、6一类，2、3一类，5、7一类;C类学生认为l、6一类，2、5一类，3、4、7一类。教师组织学生辩论：A类学生认为，两条直线的位置关系就交叉和不交叉两种;B类学生认为2和3的两条直线刚刚碰牢，5和7的两条直线才是相交;C类学生认为4看上去不交叉但延长后也是交叉的，2和5在交叉里属于特殊情况，应该单独为一类。这时有学生说，如果把每条直线都延长，1和6永远不会相交为一类，2、3、4、5、7都会相交为一类。教师让学生把每条直线都延长进行验证，最后达成了共识。

2.学生没有看到、想到时

学生的知识、能力和思维是有一定局限性的，他们在学习过程中出现没有看到或者想到的情况很正常，遇到这种情况需要教师通过追问引导学生深入展开讨论，帮助学生更加立体地掌握新知识。如学习人教版《数学》五年级上册“可能性”一课，让学生以小组为单位从一个不透明的装有4个红球2个黄球的袋子里摸球，每人摸5次，每摸之前要摇匀，每次摸出一个球按要求做好记录后放回口袋，小组成员都摸过后观察摸的结果并猜测袋子里哪种颜色的球多。大多数小组摸出的结果都是红球多，并猜测袋子里红球多，可能也会有个别小组摸出的结果是黄球多，并猜想袋子里黄球多。当学生看到袋子里的球确实是红球多后，教师可以追问：有可能出现摸出的球是黄球多的情况吗？有学生认为不可能，除非有人作弊。有学生认为有可能，跟摸大奖一样的道理，虽然摸到的可能性小但还是有可能的。通过这样的追问，让学生认识到小概率事件。

3.学生出现典型错误时

学习是一个从无到有、从少到多、从不会到会的过程，学生就是在不断出错、纠错的过程中逐步发展的。尤其出现典型错误时，教师不要强制纠错，不妨“将错就错”地进行追问，让学生在错误中认识错误、明白道理、内化知识、生成智慧。如学习人教版《数学》五年级上册“植树问题”一课，解决这个问题：李明和张华住在同一幢楼里，王奶奶从一楼走到三楼的李明家用了30秒，按照这样的速度，她从一楼走到6楼的张华家需要多少时间？大多数学生都是这样解答的：30÷3=10（秒），10×6=60（秒）。教师不必即时评价与纠错，可以顺着追问：走l层楼梯需要多少时间？从一楼到二楼有几层楼梯？需要多少时间？从一楼到三楼呢？这时很多学生忽然领悟到：从一楼到三楼只有2层楼梯，走l层楼梯要30÷2=15（秒），从一楼到六楼有5层楼梯，15×5=75（秒）。

三、学生已经理解本质时

1.学生对内容已经理解时

学生理解所学内容后需要进行知识建构，知识建构是通过同化与顺应实现的。学生在知识建构过程中需要以原有的知识经验作为基础来同化新知识，与此同时，原有的知识会因为新知识的加入而发生一定的调整或改组。这时进行追问，可以帮助学生更好地建构新知识。如学习人教版《数学》五年级下册“质数和合数”一课，当学生已经理解“质数和合数的概念，知道自然数根据因数特点可以分为l、质数和合数后，可以与之前学过的“自然数根据能否被2整除可以分为奇数和偶数”联系，并追问：质数与奇数、合数与偶数这两组非常容易混淆的概念之间有什么联系？学生经过讨论发现：质数除了2都是奇数，奇数不一定是质数;偶数除了2都是合数，合数不一定是偶数。至此，学生的脑子里对自然数建立起了更加科学、立体的知识结构。

2.学生对方法已经掌握时

检验方法有没有被掌握的途径之一是解决一些相应的实际问题，在解决实际问题时追问，能判断学生对方法掌握的熟练程度并达到巩固的目的。能力较弱者说明方法没有完全掌握，表現为能发现显性问题，具备一定的分析能力并进行简单处理。能力较强者说明方法已经掌握，表现为能发现隐藏问题，可以根据现象探求解决问题的途径并找到答案。如学习人教版《数学》六年级下册“圆柱表面积”一课，学生知道怎么求圆柱的侧面积和表面积后解决这个问题：一根圆柱形木料，底面半径是0.2m，长是2m，将它截成4段，这些木料的表面积比原木料增加了多少平方米？先让学生讨论，能力一般的学生想到用4个小圆柱表面积的和减去大圆柱表面积的方法解决，能力较弱的学生甚至想不到方法，教师追问：能直接求出增加的表面积吗？能力较强者会想到用圆柱底面面积×6的方法解决。

3.学生对思想已经感悟时

数学思想是指现实世界的空间形式和数量关系反映到人们的意识中，经过思维活动而产生的结果，是对数学事实与理论经过概括后产生的本质认识。在学生对数学思想已经感悟时追问，对思维能力提升会有促进作用。如学习人教版《数学》六年级上册“数与形”一课，让学生利用图形帮助计算“1+3+5+7+9=？”时会想到三组方法：

学生能想到上述方法并进行正确计算，说明对数形结合思想已经有所领悟，但三组方法的价值是不同的，这时可以追问学生：你认为哪种方法更好？为什么？通过讨论让学生认识到第三组是利用“梯形面积公式计算，更具有普遍意义，可以解决所有求等差数列求和的问题。

追问并不难，关键是如何才能做到精准追问。小学数学教学中精准追问要关注的地方有很多，把握精准追问的时机才能起到事半功倍的效果。

[责任编辑：陈国庆]

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。