《以数学实验提升学生数学素养》-理学论文，中学数理化论文-论文范文参考-科学狗论文网

网站首页词典首页

标题

以数学实验提升学生数学素养

范文

邱晨旭

[摘? ?要]数学实验不仅能培养学生的实验意识和创新意识，而且能提升学生的数学素养.

[关键词]数学实验;数学素养;函数图像

[中图分类号]? ? G633.6? ? ? ? [文献标识码]? ? A? ? ? ? [文章编号]? ? 1674-6058（2021）17-0010-02

数学是一门很严谨的学科.当需要计算的数据非常大、非常多的时候，可以借助计算机程序来完成.高中数学课本中就有“程序框图”内容，我们可以编一些小程序来实际操作一下.对于概率统计还有数形结合的问题，也可以直接利用网络上专门的数学软件来处理.

数学实验不能仅存在于课本附页上，它需要学生亲自动手参与操作.操作的过程也是整理书面知识的过程.一些中学使用图形计算器，利用手持计算器的绘图、计算功能做一些数学实验.网络上有很多数学软件可以替代图形计算器，比如数学软件GeoGebra.它是一个集代数与几何于一体，兼有计算与绘图功能的免费的开源软件.它占用内存小，适应性很强，电脑、手机和平板都可以安装，方便学生课后练习与探索.数学实验强调学生的参与，在实践中认识和发现数学规律，培养学生的创新意识.数学实验能帮助学生对数学的理解和掌握，让学生学会对数学的应用，提高学生学习数学的兴趣，提升学生的数学素养.下面我来举几个例子.

一、画函数图像

1.画任意函数的图像

把函数图像作为数学实验的第一节课，是为了让学生尽快熟悉软件的操作，同时也是为了建立学生的自信心.操作方式很简单，直接在指令栏中输入函数表达式，然后按Enter键即可.例如，输入“[f（x）=x3-2x+1]”，然后按Enter键，即可绘制“[f（x）=x3-2x+1]”的图像.这节课从绘制简单的初等函数图像开始，到分段函数及复合函数，最后由学生自己随意发挥，随意写出函数解析式，绘制它的图像.这种模式突破了对函数的刻板印象，使得学生的信心和好奇心大增，加深了对函数的理解.

2.画动态函数图像

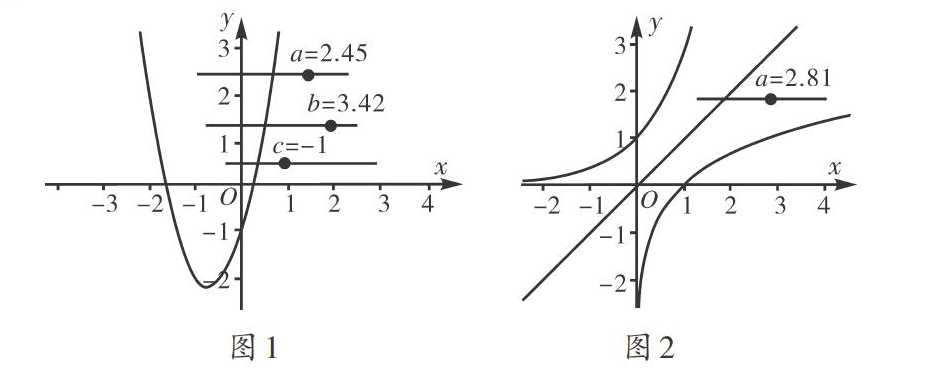
我们经常研究二次函数“[f（x）=ax2+bx+c]”中，参数[a， b， c]对函数图像的影响，所以这节课主要通过制作动态滑杆的方式，来讨论参数对函数图像的影响.操作方式：先制作动态滑杆[a， b， c]，范围均为[-5， 5]，[a≠0].然后在输入框中输入“[f（x）=ax2+bx+c]”，按Enter键即可.如图1所示，拖动滑杆[a， b， c]，观察图形变化.让学生根据图像总结，参数[a， b， c]对二次函数图像的开口方向及大小、对称轴、顶点坐标的影响.

接下来把这种方法平移到幂函数、指数函数、对数函数和三角函数上.根据函数解析式的特点，先制作动态滑杆，确定参数的取值范围，输入函数，然后拖动滑杆，观察函数图像变化，总结规律，与课本上的知识互相印证.底数相同时，指数函数与对数函数互为反函数，它们的图像关于直线[y=x]对称，所以制作动态指数函数与对数函数可以用同一个参数.把这两个函数图像放在一起，它们的动态图像始终关于直线[y=x]对称（如图2所示）.

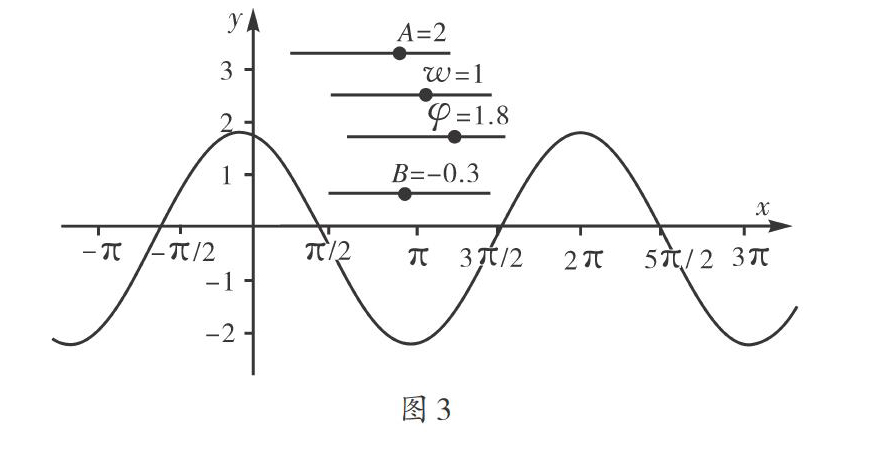
再进一步，可以利用滑动条研究函数图像的变换.如平移变换：上下平移[y=f（x）+a]，左右平移[y=f（x+a）]，伸缩变换：[y=f（ax）]、[y=af（x）].拖动滑动条可以看到函数图像的变化过程.对称变换：（1）关于[y]轴对称[y=f（-x）]、关于[x]轴对称[y=-f（x）]以及关于原点对称[y=-f（-x）];（2）含有绝对值函数的部分对称变换，如[y=f（x）]，[y=f（x）].三角函数图像的变换是高中数学的重点内容之一，所以函数图像变换的重点操作对象是三角函数[f（x）=Asin（ωx+?）+B]（如图3所示）.

二、画椭圆的图像

平面内到两定点的距离之和（大于两定点间的距离）等于定值的点的集合就是椭圆.实验操作：先在绘图区选定圆心[F1]和一点画一个圆，在圆上取一点[A]，圆内取一点[F2]（不同于圆心），连接[AF2]、[AF1]，作[AF2]的中垂线交[AF1]于点[P]，连接[PF2].

实验操作与探究：

（1）用鼠标按住点[A]，沿着圆周拖动，观察[P]点的轨迹.任意拖动绘图区中的点[F1]和点[F2]，观察点[P]的轨迹（如图4所示）.

（2）点[F1]、点[F2]不动，仅拖动点[A]，度量线段[PF1 ，? PF2]，[F1F2]的长度，计算[PF1+PF2].问：[P]点的轨迹是什么形状？与椭圆的定义有什么样的关系？拖动点[F1]对椭圆形状有什么影响？线段[PF1]的长度最大值是多少，此时[P]点在椭圆的什么位置上？

结论：通过上面的操作可以看出[P]点的轨迹就是椭圆，符合椭圆的定义.除了这种方法外，椭圆的制作方法有很多种.比如利用工具栏中的椭圆工具，或者直接在指令框中输入“[x2a2+y2b2=1]”也可以画出椭圆.椭圆以点[F1]和点[F2]为焦点，[PF1+PF2=2a].拖动点[F1]会改变椭圆的圆扁程度.这些都是椭圆中的基本量，大家可以通过GeoGebra来研究基本量之间的数量关系.

下面我们进一步探讨椭圆的有关内容.

（3）在指令框中输入“面积（椭圆c）”按Enter即可得到椭圆的面积.计算[πab]的值与椭圆的面积进行比较.

结论：由上述计算的结果得到椭圆的面积等于[πab].当[a=b]时，点[P]的轨迹就是半径为[a]的圆，圆的面积[πr2=πa2].

我们发现椭圆的面积公式与圆的面积公式是类似的.这个结论非常有意思，但是要等到大学学了高等数学之后才能给大家解释清楚.通过GeoGebra软件，我们可以验证许多猜想.比如大家知道圆的切割线定理，而椭圆与圆有许多相似的地方，那么椭圆中是否也有这样的结论呢？大家可以通过实验操作来判断这个结论是不成立的，如图5所示.

（4）椭圆的光学性质.从椭圆的一个焦点发出的光线，经过椭圆反射后，反射光线会经过椭圆的另一个焦点.让学生通过GeoGebra软件来验证这个性质.操作方式：利用橢圆工具，取两个焦点[F1]、[F2]及椭圆上一点[P]作出一个椭圆，连接[PF1]，[PF2].过点[P]作椭圆的切线，度量[PF1]，[PF2]与切线所成的角度（如图6所示）.探究结论：[PF1]，[PF2]与切线所成的角度相等，即反射角入射角与相等，从而证明了椭圆的光学性质.

由上面实验操作，学生掌握了如何利用GeoGebra探讨椭圆性质.椭圆的焦点三角形问题、椭圆的切线方程等问题留给学生课下自主探索.

通过使用GeoGebra软件，学生深入理解所学的数学知识.在实验过程中，学生注意到了一些平时容易忽视的细节，梳理了知识点的联系，完善了自己的知识系统.学生还领略到了科技带给我们的便利.数学实验要让学生自己动手，运用计算机解决具体问题.关键环节是上机操作，强调学生的参与性，学生在实践中认识和发现数学规律.整个操作过程并不是完全模仿教师的操作过程，有一些环节需要学生自己思考操作.

数学实验培养了学生的实验意识.学生可以通过实验来验证自己的猜想是否正确.数学实验为解决问题提供了一种途径.实验的过程也是学生输出自己想象的过程.或许想象的内容不正确，关键是这些想法有了输出的空间，他们可以反复实验，不断地去伪存真.这个过程培养了学生的动手操作能力、独立思考能力、探索精神和创新意识.

[? ?参? ?考? ?文? ?献? ?]

[1]? 沈翔.身边的数学辅导员：用GeoGebra领悟平面几何[M].北京：高等教育出版社，2017.

[2]? 王贵军.GeoGebra与数学实验[M].北京：清华大学出版社，2017.

（责任编辑黄桂坚）

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。