吴静

[摘 要]教师应了解学生的认知基础和已有经验,从学生的实际出发,顺应学生的认知需求,努力让教学呈现真、实、透的理想状态。以“7的乘法口诀”为例,从充分了解学情、学为主体、教师主导三个方面入手,让学习看得见、真发生。
[关键词]顺学而教;乘法;口诀;迁移
[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068(2021)05-0018-03
约翰·哈蒂教授在《可见的学习》中指出,在学校中为了帮助学生获得最佳的学习结果,我们需要可见的学习。“可见”具有两层含义:一是让教师看得见学生的“学”,明确教师的主导作用;二是让学生看得见教师的“教”,使学生逐渐成为自己的老师。下面以“7的乘法口诀”为例,谈谈我的教学困惑、实施策略以及一些思考。
一、案例背景
在“7的乘法口诀”课堂教学中,多数教师通常按照“观看情境—提出问题—列加法和乘法算式—编制口诀—记忆口诀”的模式呈现。这样的教学方式虽然直接有效,但学生是带着已有的知识经验走进课堂的,在此之前,他们经历过“1-6的乘法口诀”的学习,积累了一定的学习经验,教师如果还是“复制”前面的教学方法,牵着学生走,就会挫伤学生的学习积极性。那么,学生都已经“知道”了,课该怎么上?学生“会了”又该教什么?这是让教师困惑的问题。带着以上思考,我对这节课进行了课例研究。
二、教学策略及反思
1.复习导入,方法迁移
师:前面我们学习了乘法口诀,谁能背出6的乘法口诀?6的乘法口诀有什么特征?
生1:口诀的第一个数字依次增加1,第二个数字都是6,相邻两句的得数相差1个6。6的乘法口诀有6句……
师:二六十二是什么意思?
生2:2个6相加或6个2相加。
师:请你猜想一下,7的乘法口诀又会有怎样的特征呢?
生3:相邻两句的得数都相差1个7。
生4:口诀的第二个数字都是7。
生5:口诀的第一个数字依次增加1。
生6:7的乘法口诀一共有7句。
2.自主探索,编制口诀
师:请在研学单上试着编出7的乘法口诀。
学生根据自己的实际情况选择学习方式,展开自主学习:
(1)觉得自己能够独立推导7的乘法口诀的,开始独立探究。
(2)如果有困难,可以向同桌请教。
(3)觉得无从下手的,可以和老师一起推导。
3.交流汇报,整理口诀。
(1)学生先在小组内说一说。
(2)学生小组汇报(投影展示各小组所编的口诀,其余小组的学生从所编的口诀是否正确,编口诀要注意什么等方面进行辨析)
【反思】从学生的现实起点出发,顺学而教。课堂教学要面向全体学生,必须从学生的学习起点出发,才能激发学生主动地去思考、去学习。课前我做了学情调查,发现90%的学生已经会编7的乘法口诀,其中一部分甚至能熟练背出口诀;8%的学生需要慢慢用加法计算;只有2%的学生完全不知道怎么编。基于此,我以学生的现有思维发展水平为基础,选择与学生现有发展水平相适应的学习方式,为不同学生创造适合他们的教学情境。在教学“7的乘法口诀”的过程中,我先让学生回忆6的乘法口诀的特征和意义,找到新旧知识的联系;再让学生猜想7的乘法口诀的规律,为学生学习新知搭建桥梁;然后放手让学生根据自己的实际情况自主编制口诀,交流口诀的排列规律,验证之前的猜想;最后探讨记忆口诀的方法。通过提供足够的自主学习空间和充分的交流机会,因材施教,激发学生的求知欲,让不同的学生得到不同的发展。奥苏伯尔曾明确指出,影响学习最重要的一个因素是学生已经知道了什么,我们应当根据学生原有的知识状况去进行教学。也就是说,只有正确认识学生的学习起点,顺学而教,才是最适合学生的。
4.自主建构,理解意义
师:会编口诀还要知道口诀的意义,你能用自己喜欢的方式把“二七十四”这句口诀的意思表示出来吗?
(学生在研学单上自主完成后,全班展示交流)
生1:我这样表示。(如图1)
师:大家觉得他表示的是“二七十四”这句口诀吗?你是怎么理解的?
生2:我觉得是对的。因为他每一列都画了7个圆圈,一共画了2列,有2个7,表示“二七十四”。
生3:我是横着看的,一行有2个圆圈,一共有7行,可以看成7个2,表示“二七十四”。
师:你真会观察。
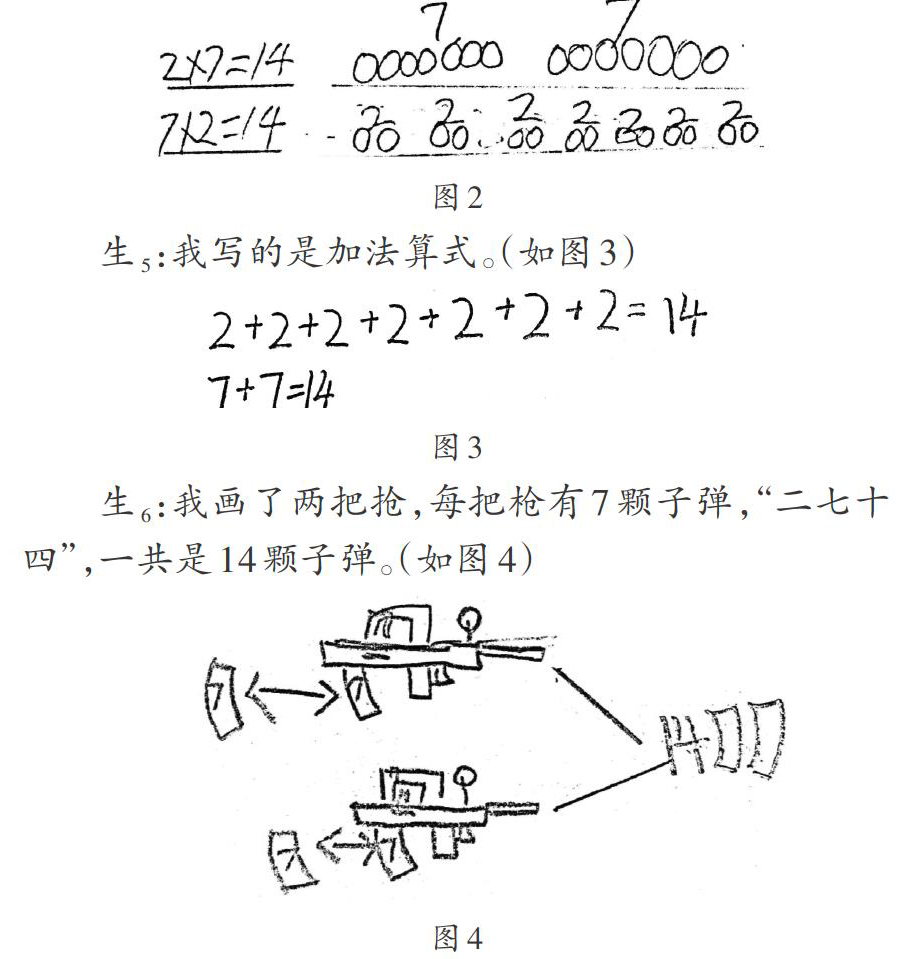
生4:老师,我画了图,还写了乘法算式2×7=14,7×2=14。(如图2)
生5:我写的是加法算式。(如图3)
生6:我画了两把抢,每把枪有7颗子弹,“二七十四”,一共是14颗子弹。(如图4)
师:吴老师还发现有位同学的作品很特殊,我们一起看一看(出示图5)。好奇怪,这是什么意思呀?
生7:吴老师,我发现你的“吴”字有7画,2个“吴”字一共有 14 画!
师:你们的“二七十四”真精彩,让吴老师大开眼界,真棒!可是这些为什么都能表示“二七十四”这句口诀呢?
生8:因为它们都是2个7相加或者7个2相加。
师(指着图 1):这个图是2个7相加,如果想表示“三七二十一”,你觉得这幅图应如何修改?
(学生继续画图表示“三七二十一”)
师:刚才我们已经理解了这两句口诀,那么剩下来的几句口诀分别表示什么意思呢?请你们先独立思考,再在小组里说一说,也可以摆一摆、画一画。
【反思】学为主体,让“学”看得见。学生是学习的主体,学习是要学习者主动参与的活动,而学生学习1-6的乘法口诀时,基本上是在教师的带领下根据加法和乘法算式来编制口诀的,很多时候,学生对口诀意义的了解是被動的,缺少内驱力。“纸上得来终觉浅”,由于他们对口诀的意义缺乏深入理解,以致在后续学习中不能灵活地应用口诀进行推理。在本环节中,我把课堂的主动权交给学生,营造自主学习的氛围,让学生用自己的方法表示口诀的含义,并主动对7的乘法口诀进行建构。通过这样的方式,学生的思维鲜活地呈现出来,有的画圆圈、爱心、三角形、手枪,有的写字,有的写算式……通过这样的形式,学生自然就会发现这些表示方法原来都指向“7个2”或者“2个7”!在经历了主动探索和归纳总结后,学生对乘法口诀的核心“几个几”的认识就上了一个台阶,因为他们在学习过程中看见了自己的“学”。
5.巧妙点拨,变式练习
出示算式题组:
(1)3×7+7=? ?(2)4×7+7=
4×7=? ? ? ? ? ?5×7=
7×4=? ? ? ? ? ? ? ? ? ? ? ? ? ?7×5=
师:猜猜这两组算式的结果有什么特点?
生1:同一组3个算式的得数相等。
师:大家都来算一算。
(学生独立完成,验证得数是否相等)
师:想一想,为什么得数会相等呢?
生2:我发现3个7加1个7是4个7,4×7和7×4都可以表示4个7,“四七二十八”,所以第一组的得数都是28。
生3:我发现第二组都是5个7,“五七三十五”,所以得数都是35。
师:同学们真会动脑筋!下面的第三组算式你会填么?
(3)5×7+7=( ? )×(?)
=( )×(?)
(学生独立完成后,全班交流)
生4:我填的是6×7和7×6,因为5个7和1个7合起来是6个7。
师:你们会举一反三了,真棒!下面的第四组算式又可以怎么变呢?
(4)7×6=(?)×(?)+(?)
=(?)×(?)-(?)
生5:我填的是7×5+7,因为5个7加1个7是6个7,就是7×6。
生6:我的答案是7×4+7×2,因为4个7加2个7也等于6个7。
生7:我把7×6看作7个6,因为6个6加1个6是7个6,所以我写了6×6+6。
生8:我是用7个7减去1个7得到6个7,所以我填了7×7-7。
……
师:同学们都非常善于思考,为你们点赞!
【反思】教为主导,让“教”看得见。教师要起主导作用,要能诱导学生主动学习,探究知识的过程。教师的“教”要让学生可见,也就是教给学生学习的方法,让他们能够利用这些方法自主学习。在这个环节,我先让学生猜想第一、二组算式会有怎样的结果,激发学生的探索欲,学生很快发现同一组3个算式的得数相等,经过验证确实如此,那么学生自然就会去想:为什么相等呢?学生在充分的思考和交流中发现每组算式都可以表示几个7,并总结了规律:有些乘加算式可以通过几个几的方式转化成乘法算式。在此基础上,学生完成变式练习“5×7+7=()×()=
()×()”就水到渠成了。为了进一步提升学生思维的深度,我又提供了更开放的变式练习“7×6=()×()+( )=()×( )-(?)”,学生的答案五花八门:7×5+7、7×4+7×2、6×6+6、7×7-7……在循序渐进中,学生头脑中的几个几“活”了起来、“动”了起来,对乘法意义的理解达到了前所未有的高度,运用乘法口诀就更加得心应手了。在后续的学习中,我发现有学生甚至会用几个几相加的方法计算两位数乘一位数了,还有学生主动去探究9的乘法口诀的规律……学生看到了教师的“教”和自己的“学”,进而主动去学,“教”和“学”灵动互见,学习就自然发生了。
作为教师,首先要准确把脉学生已经知道了什么,还要学什么,然后为学生提供充分的学习材料,引导学生怎么学,让学生在学习过程中看见自己的“学”。总之,“教”要对学生可见,“学”要对教师可见,当“学什么”可见时,学习就真正发生了。
[ 參 考 文 献 ]
[1] 约翰·哈蒂.可见的学习——最大程度地促进学习(教师版)[M].金莺莲,洪超,裴新宁,译.北京:教育科学出版社,2015.
[2] 贲友林.学为中心:让学生有学习效能感——《8的乘法口诀》教学解读[J].教育视界,2018(20).
(责编 李琪琦)
- 篮球比赛中小前锋技战术发展趋势的研究
- 经典名著的跨媒介阅读与交流
- 老年人学习需求类型的研究
- 海南尖峰岭国家森林公园公共服务存在的问题及对策
- 门诊健康管理小组在老年哮喘患者自我管理中的作用
- 大学生社会主义核心价值观的形成规律与教育对
- 浅析高校辅导员落实立德树人根本任务
- 高职辅导员思想政治教育能力及提升途径
- 以教学改革为中心,不断提高“形势与政策”课有效性
- “互联网+”视阈下高校学生立德树人教育实践研究
- 信息技术支持下小学生诚信教育策略探讨
- 提高应用型高校思政课实效强化学生核心价值观的培育
- “互联网+”背景下大学生思想政治教育主体互动模式的构建
- 高校英语教师思辨能力存在的问题及应对策略
- “以人为本”视角下新加坡教师培训的特色及其启示
- MOOC条件下O2O混合教学模式中的教师角色建构及策略
- 临床医学专业本科生“辅导员—导师制”教育管理模式的实施途径
- 中学寄宿学生心理健康状况调查分析
- 中学生参与啦啦操运动动机与效果比较研究
- 大学生阅读行为、自我学习与成长满意度调查研究
- 地方高校研究生生源状况的分析及思考
- 江苏地区艺术类专业大学生“校园贷”现象的调研报告
- 非英语专业本科生四、六级成绩下滑与学习动机变化相关性调查研究
- 道安“五失本”中的文质思想
- 基于经济学思维培养的创新创业课程建设探索
- dingier
- dingies
- dingiest
- dingily
- dinginess
- dinginesses
- dingy
- dining
- dining-out
- dining out
- dining-room
- diningroom
- dining room
- dining-rooms
- dining rooms
- dinned
- dinner
- dinner-jacket
- dinner jacket
- dinner jackets
- dinnerless
- dinner party
- dinners
- dinnery
- dinning
- 御风客
- 御风而行的神车
- 御风鼓浪
- 御香
- 御马
- 御驾
- 御驾亲征
- 御驾亲蒸(征)
- 御魑
- 御魑魅
- 御麦
- 御龙膏之酒,倚云和之瑟
- 徧
- 徨
- 徨徨
- 復
- 復廟
- 循
- 循习
- 循仍
- 循例
- 循例封官
- 循依
- 循俗
- 循分